Chapter 7 Resampling and simulation in R

In this chapter we will use R to undestand how to resample data and perform numerical simulations.

7.1 Generating random samples (Section 7.1)

Here we will generate random samples from a number of different distributions and plot their histograms.

nsamples <- 10000
nhistbins <- 100

# uniform distribution

p1 <-
  tibble(
    x = runif(nsamples)
  ) %>% 
  ggplot((aes(x))) +
  geom_histogram(bins = nhistbins) + 
  labs(title = "Uniform")

# normal distribution
p2 <-
  tibble(
    x = rnorm(nsamples)
  ) %>% 
  ggplot(aes(x)) +
  geom_histogram(bins = nhistbins) +
  labs(title = "Normal")

# Chi-squared distribution
p3 <-
  tibble(
    x = rnorm(nsamples)
  ) %>% 
  ggplot(aes(x)) +
  geom_histogram(bins = nhistbins) +
  labs(title = "Normal")

# Chi-squared distribution
p3 <-
  tibble(
    x = rchisq(nsamples, df=1)
  ) %>% 
  ggplot(aes(x)) +
  geom_histogram(bins = nhistbins) +
  labs(title = "Chi-squared")

# Poisson distribution
p4 <-
  tibble(
    x = rbinom(nsamples, 20, 0.25)
  ) %>% 
  ggplot(aes(x)) +
  geom_histogram(bins = nhistbins) +
  labs(title = "Binomial (p=0.25, 20 trials)")


plot_grid(p1, p2, p3, p4, ncol = 2)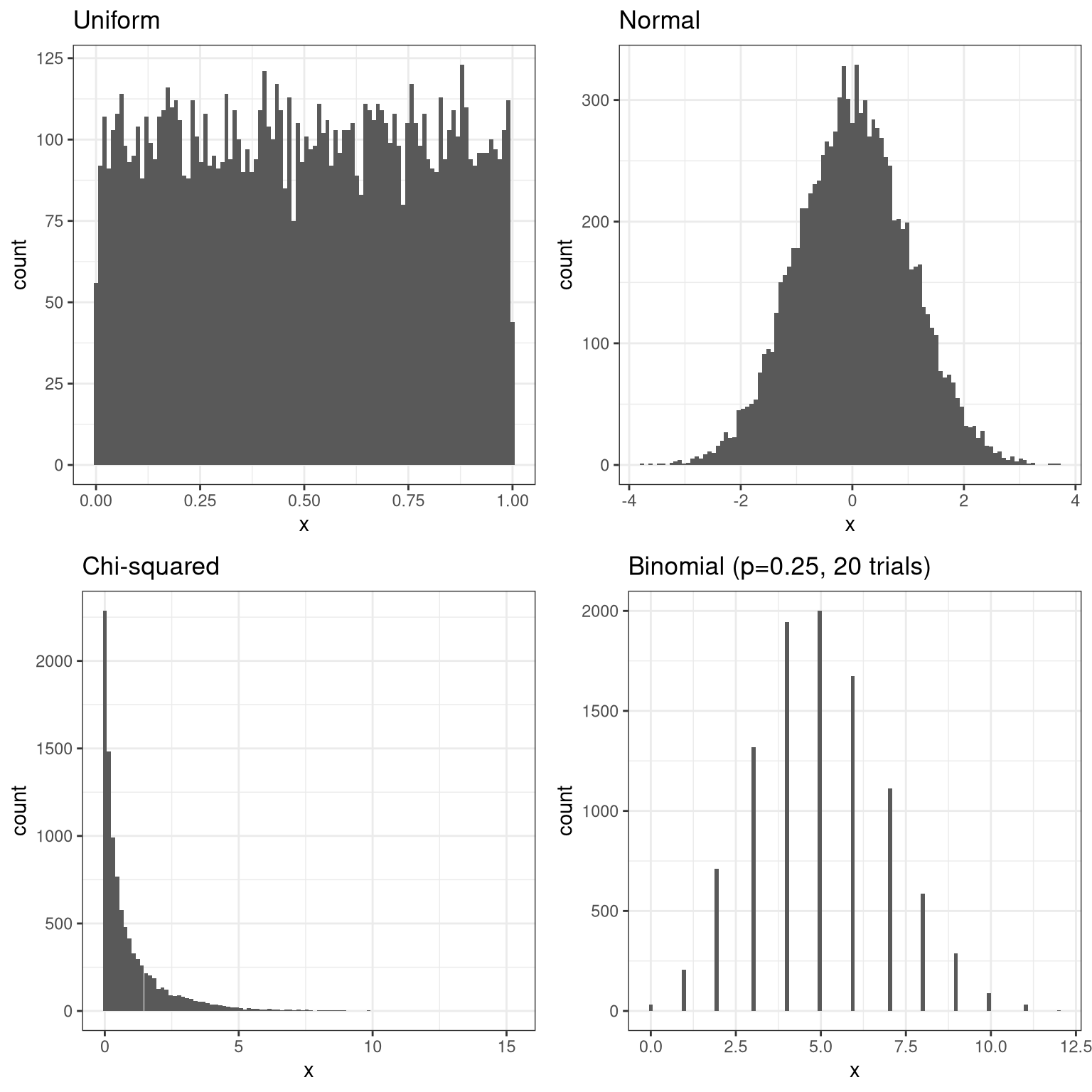

7.2 Simulating the maximum finishing time

Let’s simulate 150 samples, collecting the maximum value from each sample, and then plotting the distribution of maxima.

# sample maximum value 5000 times and compute 99th percentile
nRuns <- 5000
sampSize <- 150

sampleMax <- function(sampSize = 150) {
  samp <- rnorm(sampSize, mean = 5, sd = 1)
  return(tibble(max=max(samp)))
}

input_df <- tibble(id=seq(nRuns)) %>%
  group_by(id)

maxTime <- input_df %>% do(sampleMax())

cutoff <- quantile(maxTime$max, 0.99)


ggplot(maxTime,aes(max)) +
  geom_histogram(bins = 100) +
  geom_vline(xintercept = cutoff, color = "red")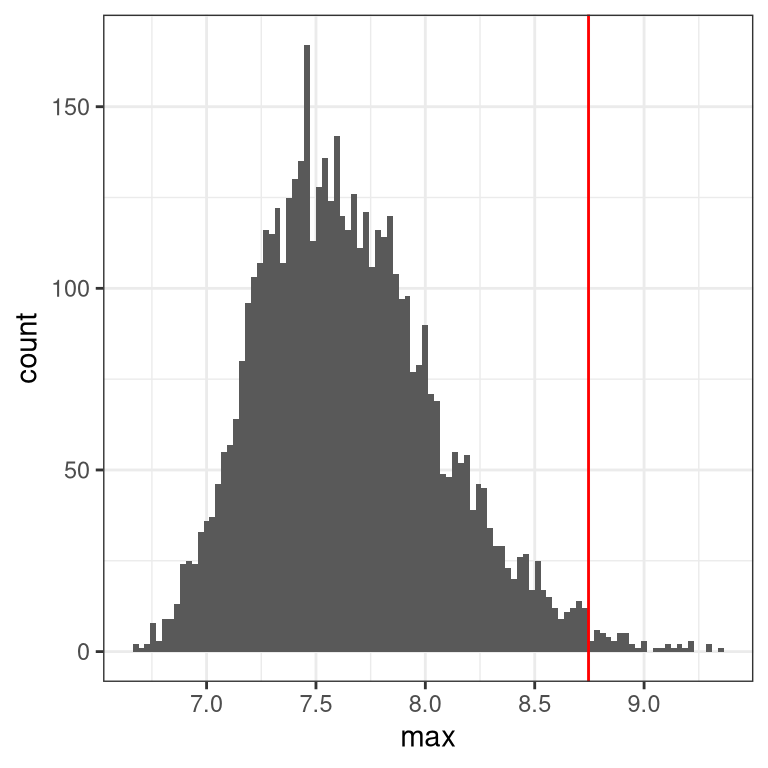

7.3 The bootstrap

The bootstrap is useful for creating confidence intervals in cases where we don’t have a parametric distribution. One example is for the median; let’s look at how that works. We will start by implementing it by hand, to see more closely how it works. We will start by collecting a sample of individuals from the NHANES dataset, and the using the bootstrap to obtain confidence intervals on the median for the Height variable.

Lower CI limit	Median	Upper CI limit
161.6	167.65	171.1