Capitulo 11 Estadística Bayesiana

En este capítulo estaremos trabajando desde el enfoque del modelado estadístico e inferencial que contrasta con el marco de prueba de hipótesis nula que vimos en el capítulo 9. Esto se conoce como “Estadística Bayesiana,” en honor al reverendo Thomas Bayes, cuyo teorema ya has visto en el capítulo 6. En este capítulo aprenderás cómo el teorema de Bayes proporciona una forma de entender los datos que resuelve muchos de los problemas conceptuales que discutimos con respecto a la prueba de hipótesis nula, mientras introduce a su vez nuevos retos.

11.1 Modelos Generativos

Digamos que estás caminando por la calle y unx amigx tuyx camina a tu lado pero no te saluda. Probablemente vas a tratar de decidir por qué pasó esto, ¿no te vieron? ¿están enojadxs contigo? ¿De repente traes una capa de invisibilidad y no te has dado cuenta? Una de las ideas básicas de la estadística Bayesiana es que queremos inferir los detalles de cómo son generados los datos, basándonos en los datos mismos. En este caso, tú quieres usar los datos (por ejemplo, el hecho de que tu amigx no te saludó), para inferir el proceso que generó esos datos (si de verdad no te vieron, cómo se sienten con respecto tuyo, etc.).

La idea detrás de los modelos generativos es que un proceso latente (que no se ha visto) genera los datos que observamos, usualmente con una cantidad de aleatoridad en el proceso. Cuando tomamos una muestra de datos de una población y estimamos el parámetro a partir de la muestra, lo que estamos haciendo en esencia es tratar de conocer el valor de la variable latente (la media de la población), la cual da lugar a través del muestreo a los datos observados (la media de la muestra). La Figura 11.1 muestra un esquema de esta idea.

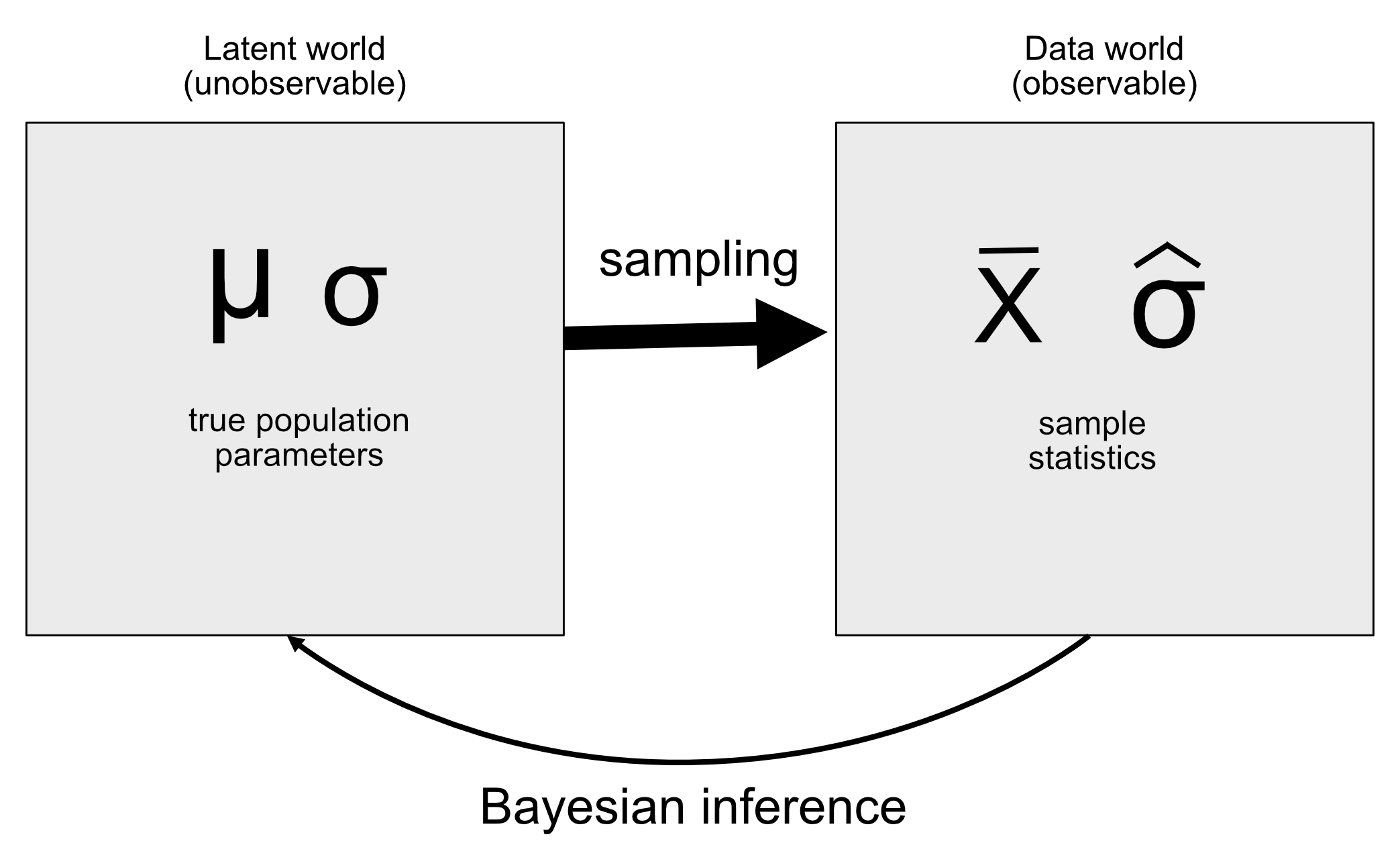
Figura 11.1: A schematic of the idea of a generative model.

Si conociéramos el valor de la variable latente, entonces debería de ser fácil reconstruir cómo deberían verse los datos observados. Por ejemplo, digamos que lanzamos una moneda que sabemos que está balanceada, por lo que podemos esperar que caiga cara el 50% de las veces que se lanza. Podemos describir la moneda con una distribución binomial con un valor de \(P_{heads}=0.5\), y luego podemos generar una muestra aleatoria de tal distribución con el fin de visualizar cómo se deberían de ver los datos. No obstante, en general estamos en la posición contraria: No sabemos el valor de la variable de interés latente, pero tenemos algunos datos que nos gustaría usar para estimarlo.

11.2 El Teorema de Bayes y la Inferencia Inversa

La razón por la cual la estadística Bayesiana tiene tal nombre es porque aprovecha el teorema de Bayes para hacer inferencias a partir de los datos sobre el proceso subyacente que generó los datos. Digamos que queremos saber si una moneda está balanceada. Para probar esto, lanzamos la moneda 10 veces y en 7 ocasiones cae en cara. Antes de esta prueba, estábamos muy seguros de que \(P_{heads}=0.5\), pero al caer cara 7 veces de 10 lanzamientos sin duda nos daría una pausa si creyéramos que \(P_{heads}=0.5\). Ya sabemos cómo calcular la probabilidad condicional de que caiga 7 o más veces en cara (de 10 veces que se lanza la moneda) si la moneda realmente está balanceada (\(P(n\ge7|p_{heads}=0.5)\)), usando la distribución binomial.

La probabilidad resultante es 0.055. Ese es un número bastante pequeño, pero este número no responde realmente a la pregunta que estamos haciendo– nos está diciendo la probabilidad de que en 7 ocasiones o más la moneda caiga en cara, dada una probabilidad particular de cara, mientras que lo que queremos saber en realidad es la probabilidad verdadera de que caiga cara en esta moneda en particular. Esto debería sonar familiar, ya que es una situación exactamente igual a la que estábamos con la prueba de hipótesis nula, la cual nos mostró la probabilidad de los datos, en lugar de la probabilidad de las hipótesis.

Recuerda que el teorema de Bayes nos provee con una herramienta que necesitamos para invertir una probabilidad condicional.

\[ P(H|D) = \frac{P(D|H)*P(H)}{P(D)} \]

Podemos pensar este teorema como si tuviéramos cuatro partes (entre paréntesis están sus nombres en inglés, y su notación matemática):

• Probabilidad previa (prior: \(P(Hipótesis)\)): Nuestro grado de creencia sobre la hipótesis H antes de ver los datos D.
• Probabilidad (Likelihood: \(P(Datos|Hipótesis)\)): ¿Qué tan probables son los datos observados D bajo la hipótesis H?
• Probabilidad marginal (marginal likelihood: \(P(Datos)\)): ¿Qué tan probables son los datos observados, combinando todas las hipótesis posibles?
• Probabilidad Posterior (posterior: \(P(Hipótesis|Datos)\)): Nuestra creencia actualizada sobre la hipótesis H, dados los datos D.

En el caso de nuestro ejemplo de lanzar la moneda:

• Probilidad previa (\(P_ {cara}\)): Nuestro grado de creencia sobre la probabilidad de que caiga en cara, que fue \(P_ {cara} = 0.5\).
• Probabilidad (\(P(\text{7 o más caras en 10 lanzamientos}|P_{cara}=0.5)\)): ¿Qué probabilidad hay de 7 o más caras de 10 lanzamientos si \(P_{cara}=0.5)\)?
• Probabilidad marginal (\(P(\text{7 o más caras en 10 lanzamientos})\)): ¿Qué probabilidades hay de que observemos 7 caras de cada 10 lanzamientos de moneda, en general?
• Probabilidad posterior (\(P_{cara}|\text{7 o más caras en 10 lanzamientos})\)): Nuestra creencia actualizada sobre \(P_{cara}\) dados los lanzamientos de moneda observados.

Aquí vemos una de las principales diferencias entre la estadística frecuentista y bayesiana. Lxs frecuentistas no creen en la idea de una probabilidad de una hipótesis (es decir, nuestro grado de creencia sobre una hipótesis); para ellxs, una hipótesis es verdadera o no lo es. Otra forma de decir esto es que para la/el frecuentista, la hipótesis es fija y los datos son aleatorios, por lo que la inferencia frecuentista se centra en describir la probabilidad de los datos dada una hipótesis (es decir, el valor p). Lxs bayesianos, por otro lado, se sienten cómodos haciendo declaraciones de probabilidad sobre datos e hipótesis.

11.3 Haciendo estimaciones Bayesianas

En última instancia, queremos utilizar la estadística bayesiana para tomar decisiones sobre las hipótesis, pero antes de hacerlo, debemos estimar los parámetros que son necesarios para tomar la decisión. Aquí recorreremos el proceso de estimación bayesiana. Usemos otro ejemplo de inspecciones (screening): la inspección de seguridad del aeropuerto. Si vuelas mucho, es solo cuestión de tiempo para que una de las inspecciones aleatorias de explosivos resulte positiva; tuve la experiencia particularmente desafortunada de que esto sucediera poco después del 11 de septiembre de 2001, cuando el personal de seguridad del aeropuerto estaba especialmente nervioso.

Lo que el personal de seguridad quiere saber es cuál es la probabilidad de que una persona lleve un explosivo, dado que la máquina ha dado positivo en la prueba. Veamos cómo calcular este valor mediante el análisis bayesiano.

11.3.1 Especificar la probabilidad previa

Para usar el teorema de Bayes, primero debemos especificar la probabilidad previa para la hipótesis. En este caso, no sabemos el número real pero podemos asumir que es pequeño. De acuerdo a la FAA, había 971,595,898 pasajeros aéreos en los Estados Unidos de América en 2017. Digamos que uno de esos viajeros llevaba un explosivo en su bolsa — esto nos daría una probabilidad previa de 1 entre 971 millones, lo cual es muy pequeño. El personal de seguridad seguramente tuvo en mente una probabilidad previa mucho mayor en los meses después del ataque del 9/11, así que diremos que su pensamiento subjetivo era que uno en un millón de viajeros traía consigo un explosivo.

11.3.2 Recolectar los datos

Los datos se componen de los resultados de las pruebas de screening de explosivos. Digamos que el staff de seguridad pasa una bolsa a través de su aparato para comprobar que sea seguro, lo pasa durante 3 veces, y da positivo en 3 de las 3 pruebas.

11.3.3 Calcular la probabilidad (likelihood)

Queremos calcular la probabilidad (likelihood) de los datos observados bajo la hipótesis de que hay un explosivo en la bolsa. Digamos que sabemos (por los fabricantes de la máquina) que la sensibilidad de la prueba es 0.99 – o sea, cuando un objeto explosivo está presente lo detectará un 99% de las veces. Para determinar la probabilidad de nuestros datos bajo la hipótesis de que un objeto explosivo está presente, podemos tratar cada prueba como un ensayo de Bernoulli (o sea, un ensayo con un resultado de verdadero o falso) con una probabilidad de éxito de 0.99, lo cual podemos modelar con una distribución binomial.

11.3.4 Calcular la probabilidad marginal (marginal likelihood)

También necesitamos saber la probabilidad (likelihood) total de los datos – esto es, el encontrar 3 positivos de 3 pruebas. Calcular la probabilidad marginal es comúnmente uno de los aspectos del análisis Bayesiano más difíciles, pero para nuestro ejemplo, es simple, ya que, podemos tomar ventaja de la forma específica del teorema de Bayes para un resultado binario que presentamos en la sección 6.7: \[ P(E|T) = \frac{P(T|E)*P(E)}{P(T|E)*P(E) + P(T|\neg E)*P(\neg E)} \]

en donde \(E\) se refiere a la presencia de explosivos y \(T\) se refiere a un resultado positivo de la prueba.

En este caso, la probabilidad marginal es una probabilidad ponderada (weighted probability) de la probabilidad de los datos en la presencia y en la ausencia de explosivos, multiplicada por la probabilidad de que haya un explosivo presente (es decir, la probabilidad previa). En este caso, digamos que sabemos (gracias al fabricante), que la especificidad de la prueba es 0.99, por lo que la probabilidad de un resultado positivo cuando no hay explosivo (\(P(T|\neg E)\)) es 0.01.

11.3.5 Calcular la probabilidad posterior

Ahora que tenemos todas las partes que necesitamos para calcular la probabilidad posterior de que un explosivo esté presente en la bolsa, dados los resultados observados de 3 positivos de 3 pruebas. Este resultado nos muestra que la probabilidad posterior de que haya un explosivo en la bolsa dadas estas pruebas positivas (0.492) está justo por debajo del 50%, de nuevo resaltando el hecho de que las pruebas para detectar eventos raros casi siempre pueden producir un gran número de falsos positivos, incluso cuando la especificidad y la sensibilidad son muy altas.

Un aspecto importante del análisis Bayesiano es que puede ser secuencial. Una vez que tenemos la probabilidad posterior de un análisis, se puede convertir en la probabilidad previa del siguiente análisis.

11.4 Estimar distribuciones posteriores

En el ejemplo anterior solamente había dos posibilidades – el explosivo estaba ahí o no – y queríamos saber cuál resultado era más probable dados los datos que teníamos. Sin embargo, en otros casos queremos usar estimaciones Bayesianas para estimar el valor numérico de un parámetro. Digamos que queremos conocer la efectividad de un nuevo medicamento para el dolor; para probar esto, podemos administrar el medicamento a un grupo de pacientes y luego preguntarles si su dolor disminuyó o no después de tomar el medicamento. Podemos usar un análisis Bayesiano para estimar la proporción de personas para las cuales el medicamento será efectivo utilizando estos datos.

11.4.1 Especificar la probabilidad previa

En ete caso, no tenemos información previa sobre la efectividad del medicamento, así que usaremos una distribución uniforme como nuestra probabilidad previa, ya que los valores son igualmente probables en una distribución uniforme. Para simplificar este ejemplo, solo veremos un subconjunto de 99 posibles valores de efectividad (de .01 a .99, en pasos de .01). Por lo que cada valor posible tiene una probabilidad previa de 1/99.

11.4.2 Recolectar algunos datos

Necesitamos algunos datos para poder estimar la efectividad del medicamento. Digamos que administramos el medicamento a 100 individuos, y encontramos que 64 responden positivamente al medicamento (responders).

11.4.3 Calcular la probabilidad (likelihood)

Podemos calcular la probabilidad (likelihood) de los datos observados bajo cualquier valor particular del parámetro de efectividad usando la función de densidad binomial. En la Figura 11.2 puedes ver las curvas de probabilidad sobre el número de respondientes (quienes respondieron positivamente al medicamento, responders) para varios valores de \(P_ {respond}\). Observando esto, parece que nuestros datos observados son relativamente más probables bajo la hipótesis de \(P_ {respond} = 0.7\), algo menos probable bajo la hipótesis de \(P_ {respond} = 0.5\), y bastante improbable bajo la hipótesis de \(P_ {respond} = 0.3\). Una de las ideas fundamentales de la inferencia bayesiana es que debemos cambiar nuestra creencia sobre los valores de nuestro parámetro de interés en proporción a qué tan probables serían los datos bajo esos valores, contrastados contra lo que creíamos acerca de los valores del parámetro antes de haber visto los datos (nuestro conocimiento previo).

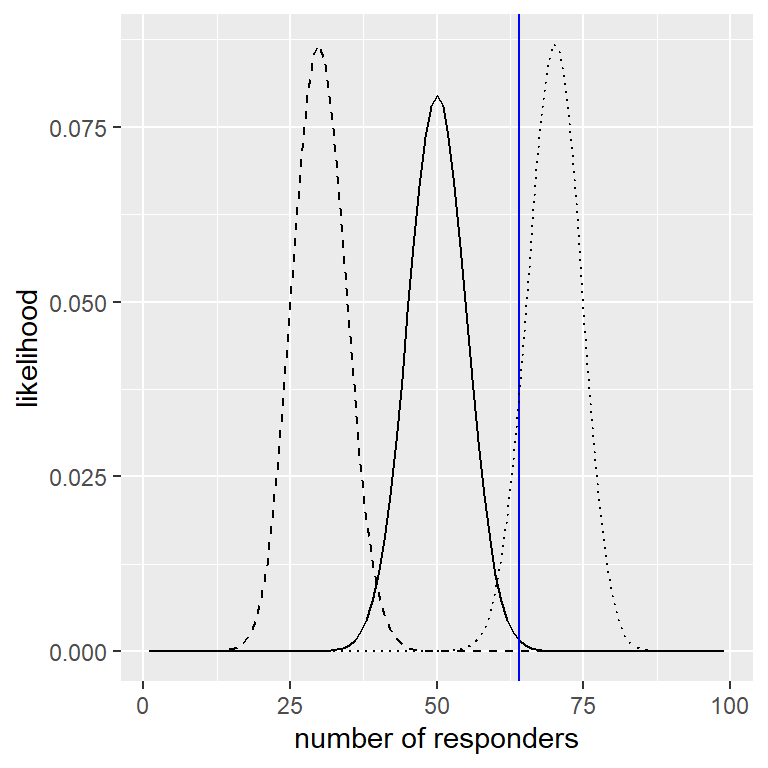
Figura 11.2: Probabilidad (likelihood) de cada número de respondientes posible bajo diferentes hipótesis (p(respond)=0.5 (línea contínua), 0.7 (línea punteada), 0.3 (línea discontinua). Los valores observados se muestran en la línea vertical.

11.4.4 Calcular la probabilidad marginal

Además de la probabilidad de los datos bajo diferentes hipótesis, necesitamos conocer la probabilidad general de los datos, combinando todas las hipótesis (es decir, la probabilidad marginal). Esta probabilidad marginal es particularmente importante porque ayuda a asegurar que los valores posteriores sean probabilidades verdaderas. En este caso, nuestro uso de un conjunto de posibles valores discretos de parámetros facilita el cálculo de la probabilidad marginal, porque podemos simplemente calcular la probabilidad de cada valor del parámetro bajo cada hipótesis y sumarlos.

11.4.5 Calcular la probabilidad posterior

Ahora tenemos todas las partes que necesitamos para calcular la distribución de probabilidad posterior a lo largo de todos los valores posibles de \(p_{respond}\), como se muestra en la Figura 11.3.

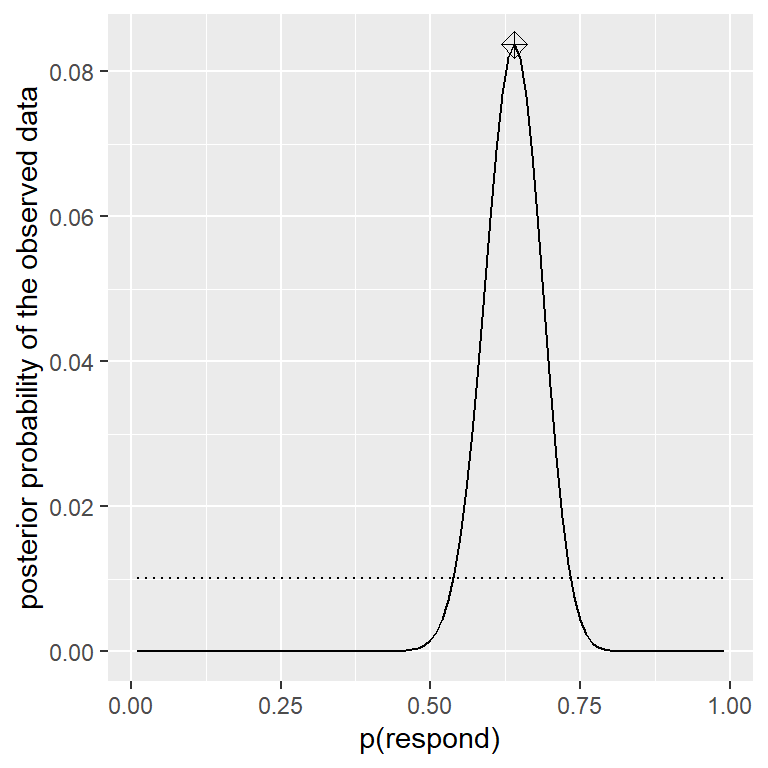
Figura 11.3: Distribución de probabilidad posterior para los datos observados graficada con la línea sólida en comparación con la distribución de probabilidad previa uniforme (línea punteada). El valor máximo a posteriori (MAP) está señalado con el símbolo de diamante.

11.4.6 Estimación máxima a posteriori (MAP, maximum a posteriori)

Dados nuestros datos, nos gustaría obtener una estimación de \(p_{respond}\) para nuestra muestra. Una forma de hacer esto es encontrar el valor de \(p_{respond}\) para el cual la probabilidad posterior es la más alta, al que nos referimos como la estimación máxima a posteriori (MAP). Podemos encontrar esto a partir de los datos en la Figura 11.3 — es el valor que se muestra con un marcador en la parte superior de la distribución. Ten en cuenta que el resultado (0.64) es simplemente la proporción de personas respondientes (quienes respondieron positivamente al medicamento) de nuestra muestra; esto ocurre porque la probabilidad a priori (probabilidad previa) era uniforme y por lo tanto no influyó en nuestra estimación.

11.4.7 Intervalos de credibilidad

Frecuentemente nos gustaría saber no solo una estimación única para la probabilidad posterior, sino un intervalo en el que confiamos que la probabilidad posterior caerá. Anteriormente discutimos el concepto de intervalos de confianza en el contexto de la inferencia frecuentista, y podrás recordar que la interpretación de los intervalos de confianza fue particularmente complicada: era un intervalo que contendrá el valor del parámetro el 95% del tiempo. Lo que realmente queremos es un intervalo en el que estemos segurxs que el verdadero parámetro estará incluido, y las estadísticas bayesianas pueden darnos ese intervalo, al que llamamos intervalo de credibilidad.

La interpretación de este intervalo de credibilidad está mucho más cerca de lo que esperábamos que pudiéramos obtener de un intervalo de confianza (pero que no obtuvimos): nos dice que hay un 95% de probabilidad de que el valor de \(p_{respond}\) se encuentre entre estos dos valores. Es importante destacar que, en este caso, muestra que tenemos una alta confianza en que \(p_{respond} > 0.0\), lo que significa que el medicamento parece tener un efecto positivo.

En algunos casos el intervalo de credibilidad puede ser calculado numéricamente basado en una distribución conocida, pero es mucho más común generar un intervalo de credibilidad al muestrar de la distribución posterior y luego calcular cuantiles de las muestras. Esto es particularmente útil cuando no tenemos una forma sencilla de expresar la distribución posterior numéricamente, que es común en un análisis de datos Bayesiano real. Uno de estos métodos (muestreo de rechazo, rejection sampling) se explica con más detalle en el Apéndice al final de este capítulo.

11.4.8 Efectos de diferentes probabilidades previas

En el ejemplo anterior usamos una probabilidad previa plana, lo cual quiere decir que no teníamos ninguna razón para creer que algún valor en particular de \(p_{respond}\) era más o menos probable. Sin embargo, digamos que en su lugar hubiéramos comenzado con algunos datos previos: En un estudio previo, investigadores habían puesto a prueba a 20 personas y habían encontrado que 10 de ellas respondieron positivamente. Esto nos habría llevado a comenzar con la creencia previa de que el tratamiento tiene efecto en el 50% de las personas. Podemos hacer el mismo cálculo que en el anterior, pero usando la información de nuestro estudio anterior para informar nuestra probabilidad previa (ve el panel A en la Figura 11.4).

Nota que la probabilidad y la probabilidad marginal no cambiaron - solamente cambió la probabilidad previa. El efecto del cambio en la probabilidad previa fue jalar la probabilidad posterior más cerca de la masa de la nueva probabilidad previa, la cual está centrada en 0.5.

Ahora veamos qué pasa si llegamos al análisis con un conocimiento previo más fuerte aún. Digamos que en lugar de haber observado con anterioridad a 10 pesonas que respondieron positivamente de 20, el estudio previo había puesto a prueba a 500 personas y encontró 250 que respondieron positivamente. Esto en principio nos debería de dar una probabilidad previa más fuerte, y como vemos en el panel B de la Figura 11.4, eso es lo que pasa: La probabilidad previa está mucho más concentrada alrededor de 0.5, y la probabilidad posterior está mucho más cerca de la probabilidad previa. La idea general es que la inferencia Bayesiana combina la información de la probabilidad previa y la probabilidad (likelihood), ponderando el peso relativo de cada una.

Este ejemplo también destaca la naturaleza secuencial de los análisis Bayesianos – la probabilidad posterior de un análisis puede tornarse en la probabilidad previa del siguiente análisis.

Finalmente, es importante destacar que si las probabilidades previas son lo suficientemente fuertes, pueden abrumar completamente a los datos. Digamos que tienes una probabilidad previa absoluta en donde \(p_{respond}\) es 0.8 o más, por lo que defines la probabilidad previa de todos los demás valores a cero. ¿Qué pasa entonces cuando calculamos la probabilidad posterior?

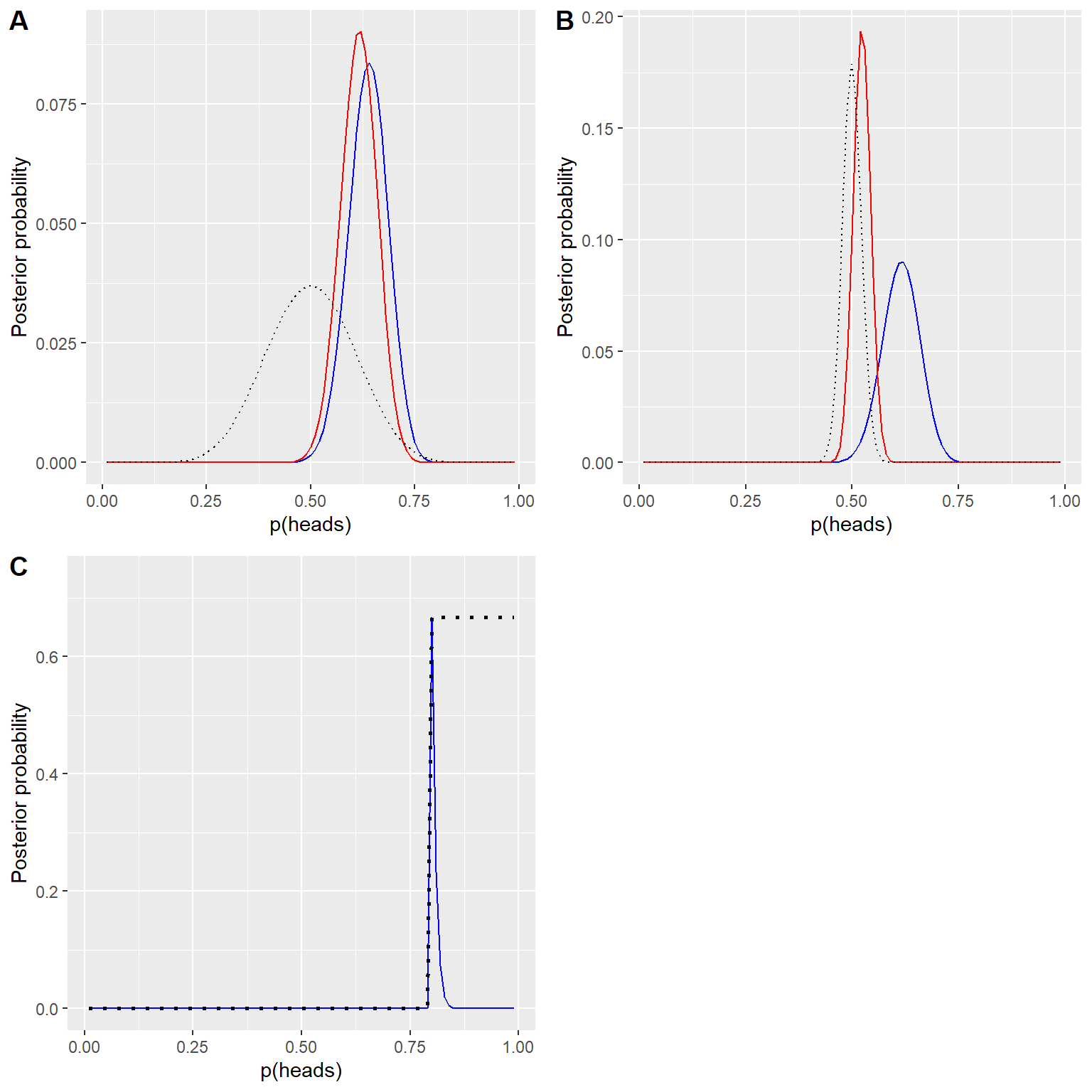
Figura 11.4: A: Efectos de probabilidades previas sobre la distribución posterior. La distribución posterior original qur se basó en una probabilidad previa plana se muestra en azul. La probabilidad previa basada en la observación de 10 respondientes de un total de 20 personas está graficada con la línea negra punteada, y la probabilidad posterior usando esta probabilidad previa está graficada en rojo. B: Efectos de la fuerza de la probabilidad previa sobre la distribución posterior. La línea azul muestra la probabilidad posterior obtenida usando una probabilidad previa basada en 50 respondientes de un total de 100 personas. La línea negra punteada muestra la probabilidad previa basada en 250 respondientes de 500 personas, y la línea roja muestra la probabilidad posterior basada en esta probabilidad previa. C: Efectos de la fuerza de la probabilidad previa sobre la distribución posterior. La línea azul muestra la probabilidad posterior obtenida usando una probabilidad previa absoluta que indica que p(respond) es 0.8 o mayor. La probabilidad previa se muestra con la línea negra punteada.

En el panel de C de la Figura 11.4 observamos que hay una densidad cero en la probabilidad posterior para cualquiera de los valores en donde la probabilidad previa se ha puesto en cero - los datos se ven abrumados por el valor previo absoluto.

11.5 Elegir una probabilidad previa

El impacto de las probabilidades previas en el resultado de las inferencias es uno de los aspectos más controversiales de la estadística Bayesiana. ¿Cuál es la probabilidad correcta a usar? Si la elección de probabilidad previa determina los resultados (es decir, la probabilidad posterior), ¿cómo puedes estar segurx que los resultados son confiables? Estas son preguntas difíciles, pero no deberíamos de retroceder solamente porque nos enfrentemos con preguntas difíciles. Como lo discutimos previamente, los análisis Bayesianos nos dan resultados interpretables (intervalos de credibilidad, etc.). Esto nos debería de inspirar a pensar seriamente sobre estas preguntas, y así poder llegar a resultados que sean razonables e interpretables.

Hay varias formas de elegir probabilidades previas, que (como vimos anteriormente) pueden afectar las inferencias resultantes. A veces tenemos una probabilidad previa muy específica, como en el caso en el que esperábamos que nuestra moneda saliera cara el 50% de las veces, pero en muchos casos no tenemos un punto de partida tan sólido. Las probabilidades previas no informativas (Uninformative priors) intentan influir lo menos posible en la probabilidad posterior resultante, como vimos en el ejemplo anterior con probabilidad uniforme. También es común usar probabilidades previas débilmente informativas (o probabilidades previas por defecto, weakly informative priors o default priors), que influyen en el resultado sólo muy levemente. Por ejemplo, si hubiéramos usado una distribución binomial basada en el resultado de una cara de dos lanzamientos de moneda, la probabilidad previa se habría centrado alrededor de 0.5, pero bastante plana, influyendo en la probabilidad posterior sólo ligeramente. También es posible utilizar probabilidades previas basadas en la literatura científica o datos preexistentes, que llamaríamos probabilidades previas empíricas (empirical priors). En general, sin embargo, nos ceñiremos al uso de probabilidades previas no-informativas / poco-informativas, ya que generan la menor preocupación de influir en nuestros resultados.

11.6 Prueba de hipótesis Bayesiana

Habiendo aprendido cómo realizar la estimación bayesiana, ahora pasamos al uso de métodos bayesianos para la prueba de hipótesis. Digamos que hay dos políticos que difieren en sus creencias sobre si el público está a favor de un impuesto extra para apoyar los parques nacionales. El senador Smith piensa que solo el 40% de la gente está a favor del impuesto, mientras que el senador Jones cree que el 60% de la gente está a favor. Organizan una encuesta para probar esto, que pregunta a 1000 personas seleccionadas al azar si apoyan tal impuesto. Los resultados son que 490 de las personas de la muestra encuestada estaban a favor del impuesto. Con base en estos datos, nos gustaría saber: ¿Los datos respaldan las afirmaciones de un senador sobre el otro y en qué medida? Podemos probar esto usando un concepto conocido como el factor de Bayes (Bayes Factors), que cuantifica qué hipótesis es mejor comparando qué tan bien predicen los datos cada una de las hipótesis.

11.6.1 Factores de Bayes

El factor de Bayes caracteriza la probabilidad relativa de los datos bajo dos hipótesis diferentes. Es definido como:

\[ BF = \frac{p(data|H_1)}{p(data|H_2)} \]

para dos hipótesis \(H_1\) y \(H_2\). En el caso de nuestros dos senadores, sabemos cómo calcular la probabilidad de los datos bajo cada hipótesis utilizando la distribución binomial; supongamos por el momento que nuestra probabilidad previa de que cada senador esté en lo correcto es la misma (\(P_{H_1} = P_{H_2} = 0.5\)). Pondremos al senador Smith en el numerador y al senador Jones en el denominador, de modo que un valor mayor que uno reflejará una mayor evidencia para el senador Smith, y un valor menor que uno reflejará una mayor evidencia para el senador Jones. El factor de Bayes resultante (3325.26) proporciona una medida de la evidencia que los datos proporcionan con respecto a las dos hipótesis; en este caso, nos dice que los datos apoyan al senador Smith más de 3000 veces más de lo que apoyan al senador Jones.

11.6.2 Factores de Bayes para hipótesis estadísticas

En el ejemplo anterior teníamos predicciones específicas de cada senador, cuya probabilidad pudimos cuantificar utilizando la distribución binomial. Además, nuestra probabilidad previa para las dos hipótesis era igual. Sin embargo, en el análisis de datos reales generalmente debemos lidiar con la incertidumbre acerca de nuestros parámetros, lo que complica el factor de Bayes, porque necesitamos calcular la probabilidad marginal (es decir, un promedio integrado de las probabilidades sobre todos los parámetros posibles del modelo, ponderado por su probabilidades). Sin embargo, a cambio, obtenemos la capacidad de cuantificar la cantidad relativa de evidencia a favor de la hipótesis nula frente a la alternativa.

Digamos que somos un investigador médico que realiza un ensayo clínico para el tratamiento de la diabetes y deseamos saber si un medicamento en particular reduce la glucosa en sangre en comparación con el placebo. Reclutamos un conjunto de voluntarios y los asignamos aleatoriamente al grupo de fármaco o placebo, y medimos el cambio en la hemoglobina A1C (un marcador de los niveles de glucosa en sangre) en cada grupo durante el período en el que se administró el fármaco o el placebo. Lo que queremos saber es: ¿Existe alguna diferencia entre el fármaco y el placebo?

Primero, generemos algunos datos y analicémoslos usando la prueba de hipótesis nula (ve la Figura 11.5). Luego, realicemos una prueba t de muestras independientes, que muestra que hay una diferencia significativa entre los grupos:

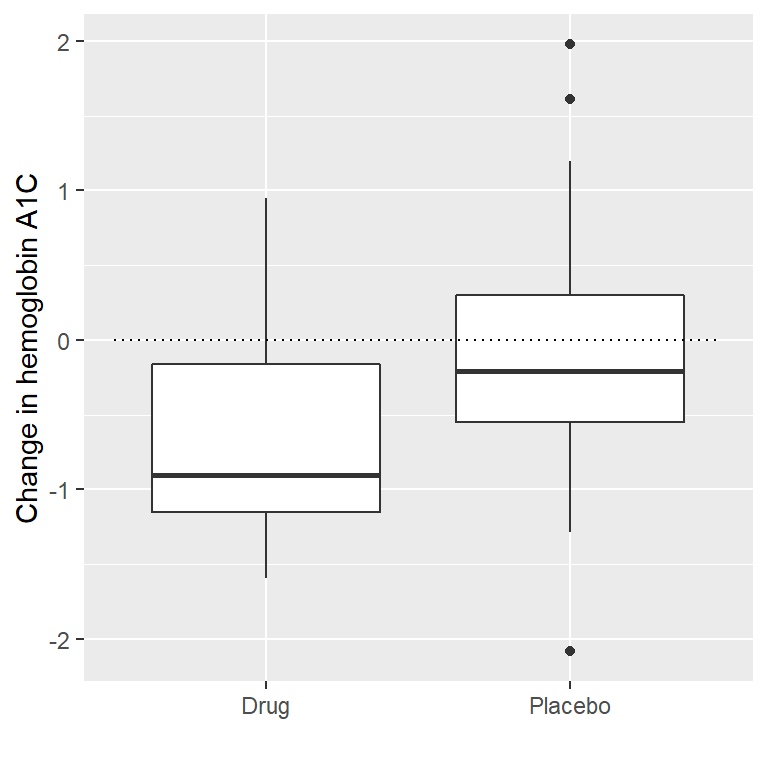
Figura 11.5: Box plots mostrando los datos de los grupos de medicamento y de placebo.

## 
##  Welch Two Sample t-test
## 
## data:  hbchange by group
## t = 2, df = 32, p-value = 0.02
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  0.11  Inf
## sample estimates:
## mean in group 0 mean in group 1 
##          -0.082          -0.650

Esta prueba nos dice que hay una diferencia significativa entre los grupos, pero no cuantifica la fuerza con la que la evidencia apoya la hipótesis nula versus la alternativa. Para medir eso, podemos calcular un factor de Bayes usando la función ttestBF del paquete de BayesFactor en R:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf    : 3.4  ±0%
## [2] Alt., r=0.707 !(0<d<Inf) : 0.12 ±0.01%
## 
## Against denominator:
##   Null, mu1-mu2 = 0 
## ---
## Bayes factor type: BFindepSample, JZS

Estamos particularmente interesadxs en el factor de Bayes para un efecto mayor que cero, que se enumera en la línea marcada “[1]” en el informe. El factor de Bayes aquí nos dice que la hipótesis alternativa (es decir, que la diferencia sea mayor que cero) es aproximadamente 3 veces más probable que la hipótesis nula puntual (es decir, una diferencia media de exactamente cero) dados los datos. Por lo tanto, si bien el efecto es significativo, la cantidad de evidencia que nos proporciona a favor de la hipótesis alternativa es bastante débil.

11.6.2.1 Pruebas unilaterales (one-sided tests)

Por lo general, estamos menos interesados en contrastar la hipótesis nula de un valor puntual específico (por ejemplo, diferencia media = 0) que en contrastar una hipótesis nula direccional (por ejemplo, que la diferencia es menor o igual a cero). También podemos realizar una prueba direccional (o unilateral, en inglés one-sided) utilizando los resultados del análisis ttestBF, ya que proporciona dos factores de Bayes: uno para la hipótesis alternativa de que la diferencia media es mayor que cero y otro para la hipótesis alternativa de que la diferencia media es menor que cero. Si queremos evaluar la evidencia relativa de un efecto positivo, podemos calcular un factor de Bayes comparando la evidencia relativa de un efecto positivo versus negativo simplemente dividiendo los dos factores de Bayes devueltos por la función:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf : 29 ±0.01%
## 
## Against denominator:
##   Alternative, r = 0.707106781186548, mu =/= 0 !(0<d<Inf) 
## ---
## Bayes factor type: BFindepSample, JZS

Ahora vemos que el factor Bayes para un efecto positivo frente a un efecto negativo es sustancialmente mayor (casi 30).

11.6.2.2 Interpretar Factores de Bayes

¿Cómo sabemos si un factor de Bayes de 2 o 20 es bueno o malo? Existe una guía general para la interpretación de los factores de Bayes sugerida por Kass & Rafferty (1995):

BF	Fuerza de la evidencia
1 to 3	No merece más que una simple mención
3 to 20	Positiva
20 to 150	Fuerte
>150	Muy fuerte

Con base en esto, aunque el resultado estadístico es significativo, la cantidad de evidencia a favor de la hipótesis alternativa frente a la hipótesis nula puntual es tan débil que apenas vale la pena mencionarla, mientras que la evidencia para la hipótesis direccional es relativamente sólida.

11.6.3 Evaluar evidencia a favor de la hipótesis nula

Debido a que el factor de Bayes está comparando evidencia para dos hipótesis, también nos permite evaluar si hay evidencia a favor de la hipótesis nula, lo cual no podríamos hacer con la prueba estándar de hipótesis nula (porque comienza con la suposición de que la nula es cierta). Esto puede ser muy útil para determinar si un resultado no significativo realmente proporciona pruebas sólidas de que no hay ningún efecto o, en cambio, solo refleja una evidencia débil en general.

11.7 Objetivos de aprendizaje

Después de leer este capítulo, debes ser capaz de:

• Describir las principales diferencias entre el análisis bayesiano y la prueba de hipótesis nula.
• Describir y realizar los pasos en un análisis bayesiano.
• Describir los efectos de diferentes probabilidades previas y las consideraciones que intervienen en la elección de una probabilidad previa.
• Describir la diferencia de interpretación entre un intervalo de confianza y un intervalo de credibilidad bayesiano.

11.8 Lecturas sugeridas

• The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy, por Sharon Bertsch McGrayne.
• Doing Bayesian Data Analysis: A Tutorial Introduction with R, por John K. Kruschke.

11.9 Apéndice:

11.9.1 Muestreo de rechazo

Generaremos muestras a partir de nuestra distribución de probabilidad posterior usando un algoritmo simple conocido como muestreo de rechazo (rejection sampling). La idea es que elegimos un valor aleatorio de x (en este caso \(p_{respond}\)) y un valor aleatorio de y (en este caso, la probabilidad posterior de \(p_{respond}\)) cada uno de una distribución uniforme. Luego aceptamos la muestra sólo si \(y < f(x)\) - en este caso, si el valor seleccionado aleatoriamente de y es menor que la probabilidad posterior real de y. La Figura 11.6 muestra un ejemplo de un histograma de muestras usando el muestreo de rechazo, junto con el intervalo de credibilidad del 95% obtenido usando este método (con los valores presentados en la Tabla ??).

	x
2.5%	0.54
98%	0.73

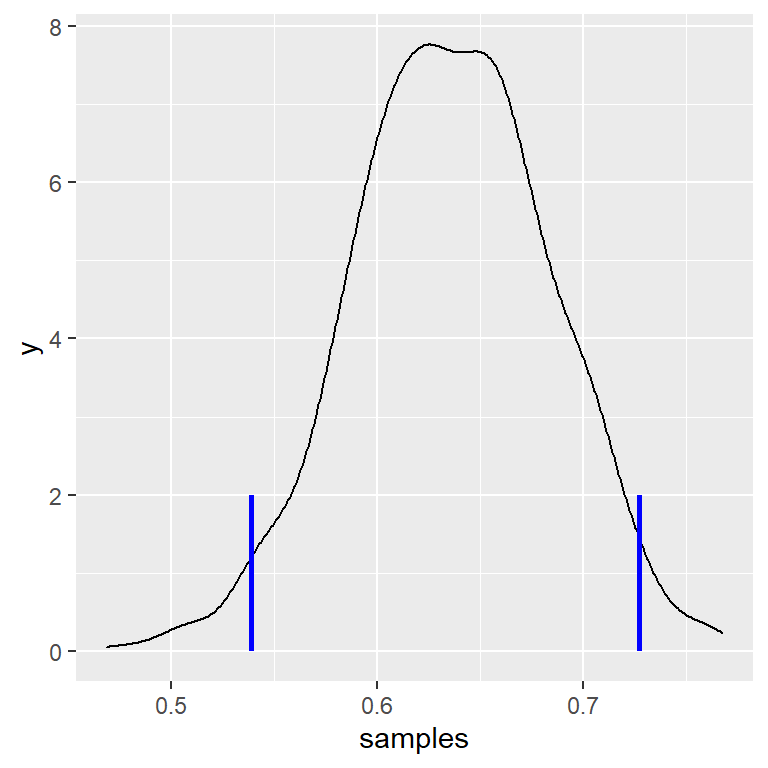
Figura 11.6: Ejemplo de muestreo de rechazo. La línea negra muestra la densidad de todos los posibles valores de p(respond); las líneas azules muestran los percentiles 2.5 y 97.5 de la distribución, que representan el intervalo de credibilidad al 95 porciento para la estimación de p(respond).