Capitulo 6 Probabilidad
La teoría de probabilidad es la rama de las matemáticas que trata con el azar y la incertidumbre. Forma parte importante de los fundamentos de la estadística, porque nos provee con las herramientas matemáticas para describir eventos inciertos. El estudio de la probabilidad inició en parte debido al interés de entender los juegos de azar, como las cartas o los dados. Estos juegos proveen de ejemplos útiles de muchos conceptos estadísticos, porque cuando repetimos estos juegos la probabilidad de diferentes resultados se mantiene (mayormente) igual. Sin embargo, existen preguntas profundas sobre el significado de la probabilidad que no abordaremos aquí; ve las Lecturas Sugeridas al final del capítulo si estás interesade en aprender más acerca de este tema fascinante y su historia.
6.1 ¿Qué es la probabilidad?
De manera informal, usualmente pensamos a la probabilidad (probability) como el número que describe la probabilidad (likelihood) de que un evento ocurra, que va de un rango desde cero (imposibilidad) a uno (certeza). A veces las probabilidades se expresarán en porcentajes, que van de un rango de cero a cien, como cuando en el pronóstico del tiempo se predice que hay un veinte por ciento de probabilidad de lluvia para hoy. En cada caso, estos números expresan qué tan probable es que suceda un evento en particular, desde la absoluta imposibilidad hasta la absoluta certeza.
Para formalizar la teoría de probabilidad, primero necesitamos definar algunos términos:
- Un experimento es cualquier actividad que produce u observa un resultado. Ejemplos son el lanzar una moneda, rodar un dado, o probar una nueva ruta al trabajo para ver si es más rápida que la vieja ruta.
- El espacio muestral es el conjunto de posibles resultados de un experimento. Los representamos enlistándolos dentro de un par de llaves ( {} ). En el caso de un lanzamiento de moneda, el espacio muestral es {cara, cruz}. En el caso de un dado de seis lados, el espacio muestral es cada uno de los posibles números que pueden aparecer: {1,2,3,4,5,6}. Para el tiempo que toma llegar al trabajo, el espacio muestral son todos los posibles números reales mayores a cero (porque no se puede llegar a algún lugar en un tiempo negativo, al menos aún no se puede). No nos preocuparemos en tratar de escribir todos esos números entre las llaves.
- Un evento es un subconjunto del espacio muestral. En principio puede ser uno o más de los posibles resultados en el espacio muestral, pero aquí nos enfocaremos principalmente en eventos elementales que consisten en exactamente un solo posible resultado. Por ejemplo, esto podría ser el obtener cara en un solo lanzamiento de moneda, sacar un 4 en un lanzamiento de dado, o tardar 21 minutos en llegar a casa en la nueva ruta.
Ahora que tenemos estas definiciones, podemos delinear las características formales de una probabilidad, las cuales fueron primero definidas por el matemático ruso Andrei Kolmogorov. Estas son las características que debe tener un valor si va a ser una probabilidad. Digamos que tenemos un espacio muestral definido por N eventos independientes, \({E_1, E_2, ... , E_N}\), y \(X\) es una variable aleatoria que denota cuál de los eventos ha ocurrido. \(P(X=E_i)\) es la probabilidad del evento \(i\):
- La probabilidad no puede ser negativa: \(P(X=E_i) \ge 0\)
- La probabilidad total de todos los resultados en un espacio muestral es 1; esto es, si tomamos la probabilidad de cada \(E_i\) y las sumamos, deben dar un total de 1. Podemos expresar esto usando el símbolo de sumatoria \(\sum\): \[ \sum_{i=1}^N{P(X=E_i)} = P(X=E_1) + P(X=E_2) + ... + P(X=E_N) = 1 \] Esto se interpreta como “Toma todos los eventos elementales N, que hemos etiquetado desde 1 hasta N, y suma sus probabilidades. Estas deben sumar 1.”
- La probabilidad de cualquier evento individual no puede ser mayor a uno: \(P(X=E_i)\le 1\). Esto es sugerido por el punto anterior; como deben de sumar uno, y no pueden ser números negativos, entonces cualquier probabilidad en particular no puede ser mayor a uno.
6.2 ¿Cómo determinamos probabilidades?
Ahora que sabemos lo que es la probabilidad, ¿cómo hacemos para realmente averiguar cuál es la probabilidad de que suceda algún evento en particular?
6.2.1 Creencia personal
Digamos que te pregunto, ¿cuál hubiera sido la probabilidad de que Bernie Sanders hubiera ganado la elección presidencial de 2016 si él hubiera sido el candidato del partido demócrata en lugar de Hilary Clinton? No podemos realmente hacer el experimento para averiguar el resultado. Sin embargo, la mayoría de las personas con conocimiento de la política estadounidense estarían dispuestos por lo menos a tratar de dar una opinión sobre la probabilidad de este evento. En muchos casos el conocimiento personal y/u opinión es la única guía que tenemos para determinar la probabilidad de un evento, pero esto no es muy satisfactorio científicamente.
6.2.2 Frecuencia empírica
Otra manera de determinar la probabilidad de un evento es el hacer un experimento muchas veces y contar cuántas veces sucedió cada evento. Podemos calcular la probabilidad de cada resultado a partir de la frecuencia relativa de los diferentes resultados. Por ejemplo, digamos que estás interesade en saber la probabilidad de lluvia en San Francisco. Primero debemos definir nuestro experimento — digamos que miraremos los datos del National Weather Service para cada día en 2017 y determinaremos si hubo lluvia en la estación del clima del centro de San Francisco. De acuerdo con estos datos, en 2017 hubo 73 días lluviosos. Para calcular la probabilidad de lluvia en San Francisco, simplemente dividimos el número de días lluviosos entre el número de días contados (365), dando \(P(lluvia en SF en 2017) = 0.2\).
¿Cómo sabemos que la probabilidad empírica nos dará el número correcto? La respuesta a esta pregunta viene de la ley de números grandes, que muestra que la probabilidad empírica se aproximará a la probabilidad verdadera conforme el tamaño de la muestra se incrementa. Podemos ver esto simulando un gran número de lanzamientos de moneda, y observando nuestra estimación de la probabilidad de que caiga cara después de cada lanzamiento. Pasaremos más tiempo discutiendo simulaciones en un capítulo posterior; por ahora, sólo asumamos que tenemos una manera computacional de generar un resultado aleatorio para cada lanzamiento de moneda.
El panel izquierdo de la Figura 6.1 muestra que conforme el número de muestras (i.e., ensayos de lanzamiento de moneda) incrementa, la probabilidad estimada de obtener cara converge en el valor verdadero de 0.5. Sin embargo, nota que las estimaciones pueden estar bastante lejos del valor verdadero cuando los tamaños de muestra son pequeños. Un ejemplo del mundo real sobre esto se puede ver en la elección especial de 2017 para el Senado de EUA en Alabama, que enfrentó al Republicano Roy Moore contra el Demócrata Doug Jones. El panel derecho de la Figura 6.1 muestra la cantidad relativa de votos reportados para cada uno de los candidatos en el curso de la tarde del día de la elección, conforme un número creciente de boletas eran contadas. Temprano en la tarde el conteo de votos era especialmente volátil, balanceándose desde una ventaja inicial grande para Jones hasta un periodo largo donde Moore tenía la ventaja, hasta que finalmente Jones tomó la delantera ganando la contienda.
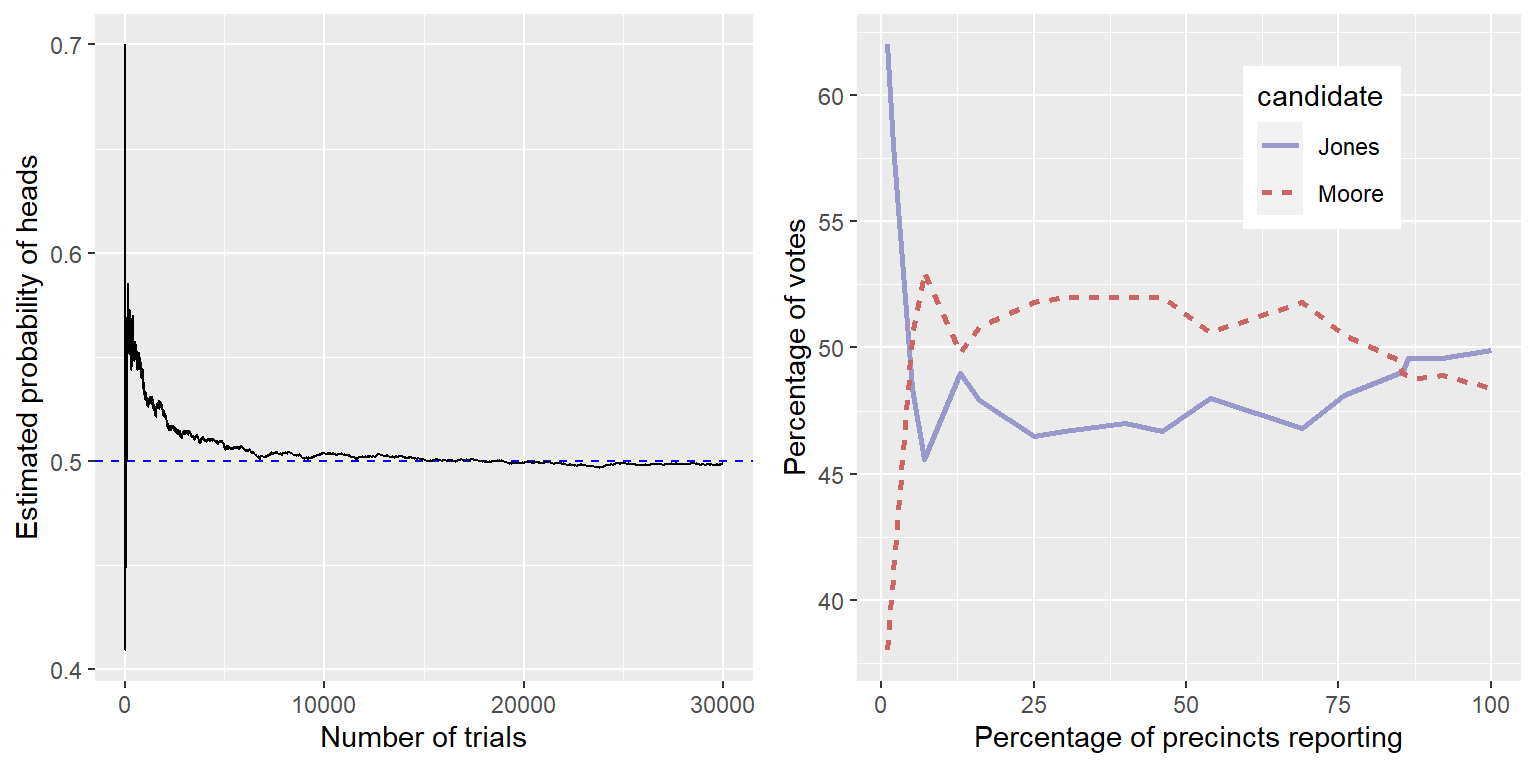
Figura 6.1: Izquierda: Una demostración de la ley de los números grandes. Una moneda fue lanzada 30,000 veces, y después de cada lanzamiento la probabilidad de obtener cara era calculada basada en el número de caras y cruces observadas hasta ese punto. Toma un aproximado de 15,000 lanzamientos para que la probabilidad se quede establecida en la probabilidad verdadera de 0.5. Derecha: Proporción relativa de votos el 12 de diciembre de 2017 durante la elección especial para el asiento de Alabama en el Senado de EUA, como una función del porcentaje de casillas electorales reportadas. Estos datos fueron transcritos de https://www.ajc.com/news/national/alabama-senate-race-live-updates-roy-moore-doug-jones/KPRfkdaweoiXICW3FHjXqI/
Estos dos ejemplos muestran que mientras las muestras grandes ultimadamente convergen en la probabilidad verdadera, los resultados de muestras pequeñas pueden estar muy equivocados. Desafortunadamente, muchas personas olvidan esto y sobreinterpretan resultados de muestras pequeñas. Esto ha sido referido como la ley de números pequeños por los psicólogos Danny Kahneman y Amos Tversky, quienes mostraron que la gente (incluso investigadores entrenados) frecuentemente se comportan como si la ley de los números grandes aplicara también en las muestras pequeñas, dando demasiada credibilidad a resultados a partir de bases de datos pequeñas. A lo largo del curso veremos ejemplos de qué tan inestables pueden ser los resultados estadísticos cuando son generados con base en muestras pequeñas.
6.2.3 Probabilidad clásica
Es poco probable que cualquiera de nosotros haya lanzado una moneda decenas de miles de veces, pero sin importar eso estamos dispuestos a creer que la probabilidad de lanzar una moneda y que caiga cara es 0.5. Esto refleja el uso de otra aproximación más al cálculo de probabilidades, al cual nos referimos como probabilidad clásica. En esta aproximación, calculamos la probabilidad directamente desde nuestro conocimiento de la situación.
La probabilidad clásica surgió del estudio de juegos de azar como los dados y las cartas. Un ejemplo famoso surgió del problema que se encontró un jugador francés que se conocía por el nombre de Chevalier de Méré. de Méré jugaba dos diferentes juegos de dados: En el primero él apostaba en la probabilidad de obtener por lo menos un seis en cuatro lanzamientos de un dado de seis lados, mientras que en el segundo juego apostaba en la probabilidad de obtener por lo menos un doble seis en 24 lanzamientos de dos dados. Él esperaba ganar dinero en ambos juegos, pero encontró que mientras que en promedio él ganaba dinero en el primer juego, realmente terminaba perdiendo dinero en promedio cuando jugaba el segundo juego muchas veces. Para entender esto buscó a su amigo, el matemático Blaise Pascal, quien es reconocido como uno de los fundadores de la teoría de probabilidad.
¿Cómo podemos entender esta pregunta usando teoría de probabilidad? En probabilidad clásica, comenzamos con una suposición de que todos los eventos elementales en el espacio muestral son igualmente probables; esto es, cuando lanzas un dado, cada uno de los posibles resultados ({1,2,3,4,5,6}) es igualmente probable que ocurra. (¡No se permiten dados cargados (o manipulados)! Considerando esto, podemos calcular la probabilidad de cualquier resultado individual como un uno dividido entre el número de resultados posibles:
\[ P(resultados_i) = \frac{1}{\text{número de resultados posibles}} \]
Para el dado de seis lados, la probabilidad de cada resultado individual es 1/6.
Esto está bien, pero de Méré estaba interesado en eventos más complejos, como lo que sucede en múltiples lanzamientos de dados. ¿Cómo calculamos la probabilidad de un evento complejo (el cual es la unión de eventos simples), como obtener un seis en el primer o el segundo lanzamiento? La unión de eventos la representamos matemáticamente usando el símbolo \(\cup\): por ejemplo, si la probabilidad de obtener un seis en el primer lanzamiento es referido como \(P(Roll6_{throw1})\) y la probabilidad de obtener un seis en el segundo lanzamiento es \(P(Roll6_{throw2})\), entonces la unión es referida como \(P(Roll6_{throw1} \cup Roll6_{throw2})\).
de Méré pensó (incorrectamente, como veremos más abajo) que simplemente podía sumar las probabilidades de cada evento individual para calcular la probabilidad del evento combinado, significando que la probabilidad de obtener un seis en el primer o segundo lanzamiento se calcularía de la siguiente manera:
\[ P(Roll6_{throw1}) = 1/6 \] \[ P(Roll6_{throw2}) = 1/6 \]
\[ El error de de Méré: \] \[ P(Roll6_{throw1} \cup Roll6_{throw2}) = P(Roll6_{throw1}) + P(Roll6_{throw2}) = 1/6 + 1/6 = 1/3 \]
de Méré creyó, basado en esta suposición incorrecta, que la probabilidad de obtener al menos un seis en cuatro lanzamientos era la suma de las probabilidades de cada lanzamiento individual: \(4*\frac{1}{6}=\frac{2}{3}\). De manera similar, creyó que dado que la probabilidad de un doble seis al lanzar un dado es 1/36, entonces la probabilidad de obtener al menos un doble seis en 24 lanzamientos de dos dados sería \(24*\frac{1}{36}=\frac{2}{3}\). Sin embargo, mientras consistentemente él ganaba dinero en la primera apuesta, perdía dinero con la segunda. ¿Por qué pasaba esto?
Para entender el error de de Méré, necesitamos presentar algunas de las reglas de la teoría de probabilidad. La primera es la regla de substracción/resta, que dice que la probabilidad de que algún evento A no suceda es uno menos la probabilidad de que el evento suceda:
\[ P(\neg A) = 1 - P(A) \]
donde \(\neg A\) significa “no A.” Esta regla se deriva directamente de los axiomas que discutimos arriba; porque A y \(\neg A\) son los únicos posibles resultados, entonces su probabilidad total debe sumar 1. Por ejemplo, si la probabilidad de obtener un uno en un solo lanzamiento es \(\frac{1}{6}\), entonces la probabilidad de obtener cualquier otro número que no fuera uno es \(\frac{5}{6}\).
Una segunda regla nos dice cómo calcular la probabilidad de un evento conjunto – esto es, la probabilidad de que ambos eventos ocurran. Nos referimos a esto como una intersección, que es representada por el símbolo \(\cap\); por lo tanto, \(P(A \cap B)\) significa la probabilidad de que ambos A y B sucedan. Nos enfocaremos en una versión de la regla que nos dice cómo calcular esta cantidad en el caso especial cuando dos eventos son independientes uno de otro; aprenderemos después exactamente qué significa el concepto de independencia, pero por ahora podemos dar por sentado que los dos lanzamientos de dados son eventos independientes. Calculamos la probabilidad de la intersección de dos eventos independientes simplemente multiplicando las probabilidades de los eventos individuales:
\[ P(A \cap B) = P(A) * P(B)\ \text{si y sólo si A y B son independientes} \] Por lo tanto, la probabilidad de obtener un seis en ambos lanzamientos de dados es \(\frac{1}{6}*\frac{1}{6}=\frac{1}{36}\).
La tercera regla nos dice cómo sumar las probabilidades - y es aquí donde vemos el origen del error de de Méré. La regla de la suma nos dice que para obtener la probabilidad de que cualquiera de dos eventos ocurran, debemos sumar las probabilidades individuales, pero luego debemos restar la probabilidad de que ocurran ambos eventos juntos:
\[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \] En un sentido, esto evita que contemos esos eventos conjuntos dos veces, eso es lo que distingue a esta regla del cálculo que de Méré había hecho incorrectamente. Digamos que queremos encontrar la probabilidad de obtener 6 en cualquiera de dos lanzamientos. De acuerdo a nuestras reglas:
\[ P(Roll6_{throw1} \cup Roll6_{throw2}) \] \[ = P(Roll6_{throw1}) + P(Roll6_{throw2}) - P(Roll6_{throw1} \cap Roll6_{throw2}) \] \[ = \frac{1}{6} + \frac{1}{6} - \frac{1}{36} = \frac{11}{36} \]
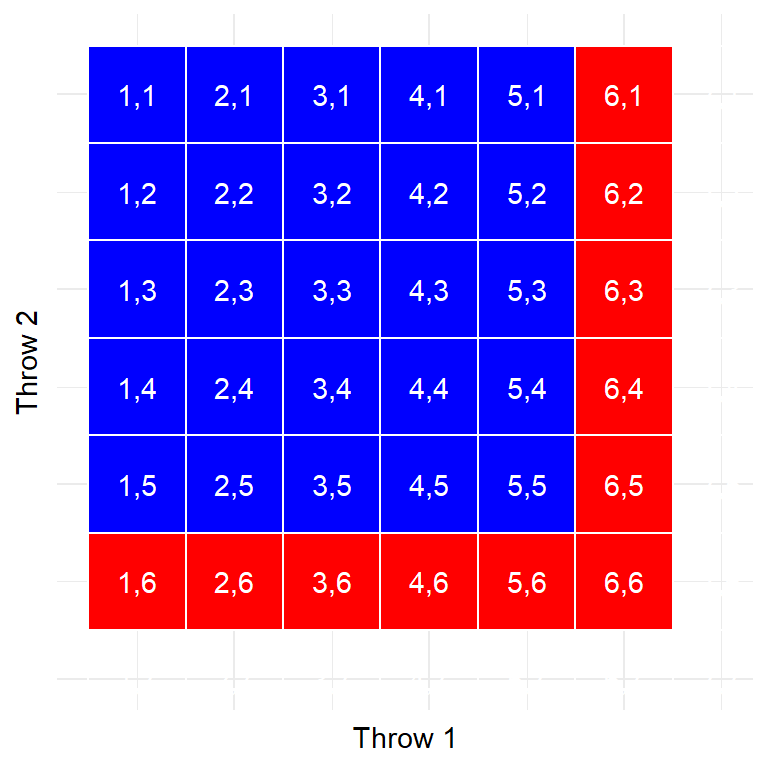
Figura 6.2: Cada celda de esta matriz representa un resultado de dos lanzamientos de un solo dado, donde las columnas representan el primer lanzamiento y las filas representan el segundo lanzamiento. Las celdas en rojo representan celdas con un seis ya sea en el primer o en el segundo lanzamiento; el resto se muestran en azul.
Usemos una representación gráfica para obtener una diferente vista de esta regla. La Figura 6.2 muestra una matriz representando todas las posibles combinaciones de resultados de dos lanzamientos de dados, y subraya las celdas que involucran un seis ya sea en el primer o en el segundo lanzamiento. Si cuentas las celdas en rojo verás que hay 11 celdas con ese resultado. Esto muestra por qué la regla de la suma da una respuesta diferente a la de de Méré; si simplemente sumáramos las probabilidades de los dos lanzamientos como él lo hizo, entonces terminaríamos contando la celda de (6,6) en ambos, cuando solamente debería contar una sola vez.
6.2.4 Resolviendo el problema de de Méré
Blaise Pascal usó las reglas de la probabilidad para idear una solución al problema de de Méré. Primero, se dio cuenta que calcular la probabilidad de al menos un evento de una combinación era complicado, mientras que calcular la probabilidad de que algo no ocurra a lo largo de varios eventos es relativamente fácil – es sólo el producto de las probabilidades de los eventos individuales. Por lo tanto, en lugar de calcular la probabilidad de al menos un seis en cuatro lanzamientos, calculó la probabilidad de ningún seis a lo largo de todos los lanzamientos:
\[ P(\text{ningún seis en cuatro lanzamientos}) \] \[ = \frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{5}{6}=\bigg(\frac{5}{6}\bigg)^4=0.482 \]
Pascal entonces usó el hecho de que la probabilidad de ningún seis en cuatro lanzamientos es el complemento de al menos un seis en cuatro lanzamientos (por lo que deben sumar uno), y usó la regla de la resta para calcular la probabilidad de interés:
\[ P(\text{al menos un seis en cuatro lanzamientos}) = 1 - \bigg(\frac{5}{6}\bigg)^4=0.517 \]
La apuesta de de Méré de que obtendría al menos un seis en cuatro lanzamientos tiene una probabilidad mayor a 0.5, lo que explica por qué de Méré ganaba dinero en esta apuesta en promedio.
¿Pero qué pasaba con la segunda apuesta de de Méré? Pascal usó el mismo truco:
\[ P(\text{no doble seis en 24 lanzamientos}) = \bigg(\frac{35}{36}\bigg)^{24}=0.509 \] \[ P(\text{al menos un doble seis en 24 lanzamientos}) = 1 - \bigg(\frac{35}{36}\bigg)^{24}=0.491 \]
La probabilidad de este resultado era ligeramente menor a 0.5, mostrando por qué de Méré perdía dinero con esta apuesta en promedio.
6.3 Distribuciones de probabilidad
Una distribución de probabilidad describe la probabilidad de todos los posibles resultados en un experimento. Por ejemplo, el 20 de enero de 2018, el jugador de basketball Steph Curry anotó sólo 2 de 4 lanzamientos libres en un juego contra los Houston Rockets. Sabemos que la probabilidad general de Curry de anotar en lanzamientos libres a lo largo de toda la temporada fue de 0.91, por lo que parece bastante poco probable que sólo hubiera anotado 50% de sus lanzamientos libres en un juego, ¿pero exactamente qué tan poco probable es? Podemos determinar esto usando una distribución de probabilidad teórica; a lo largo de este libro nos encontraremos con una variedad de estas distribuciones de probabilidad, cada una es apropiada para describir diferentes tipos de datos. En este caso, usaremos la distribución binomial, que provee una manera de calcular la probabilidad de un número de éxitos en un número de ensayos en donde se puede tener sólo un éxito o un fallo y nada intermedio (conocidos como “ensayos de Bernoulli”) dada una probabilidad conocida de éxito en cada ensayo. Esta distribución es definida como:
\[ P(k; n,p) = P(X=k) = \binom{n}{k} p^k(1-p)^{n-k} \]
Esto se refiere a la probabilidad de k éxitos en n ensayos cuando la probabilidad de éxito es p. Tal vez no estés familiarizado con \(\binom{n}{k}\), a la que nos referimos como el coeficiente binomial. El coeficiente binomial también es conocido como “n-choose-k” porque describe el número de maneras diferentes en las que uno puede elegir k elementos de un total de elementos n. El coeficiente binomial es calculado como:
\[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \] donde el signo de exclamación (!) se refiere al factorial de un número:
\[ n! = \prod_{i=1}^n i = n*(n-1)*...*2*1 \]
El operador de la multiplicación \(\prod\) es similar al operador de suma \(\sum\), excepto que multiplica en lugar de sumar. En este caso, está multiplicando juntos todos los números de uno hasta \(n\).
En el ejemplo de los lanzamientos libres de Steph Curry:
\[ P(2;4,0.91) = \binom{4}{2} 0.91^2(1-0.91)^{4-2} = 0.040 \]
Esto demuestra que dado el porcentaje de anotaciones en lanzamientos libres de Curry en la temporada, era bastante improbable que anotara sólo 2 de 4 tiros libres. Esto sólo muestra que en el mundo real efectivamente suceden cosas improbables.
6.3.1 Distribuciones de probabilidad acumuladas
Frecuentemente queremos conocer no sólo qué tan probable es un valor en específico, sino saber qué tan probable es encontrar un valor que es igualmente extremo o más extremo que cierto valor en particular; esto se volverá muy importante cuando discutamos las pruebas de hipótesis en el capítulo 9. Para contestar esta pregunta, podemos usar la distribución de probabilidad acumulada; mientras que la distribución de probabilidad estándar nos dice la probabilidad de un valor en específico, la distribución acumulada nos dice la probabilidad de un valor igual de grande o mayor (o igual de pequeño o menor) que un valor específico.
En el ejemplo del tiro libre, tal vez quisiéramos saber: ¿Cuál es la probabilidad de que Steph Curry anotara 2 o menos de un total de cuatro tiros libres, dado que su probabilidad general de anotar un tiro libre es de 0.91? Para determinar esto, podríamos simplemente usar la ecuación de probabilidad binomial y alimentarla con todos los valores posibles de k y sumarlos todos juntos:
\[ P(k\le2)= P(k=2) + P(k=1) + P(k=0) = 6e^{-5} + .002 + .040 = .043 \]
En muchos casos el número de resultados posibles podría ser demasiado grande para poder calcular la probabilidad acumulada con este método de enumerar todos los valores posibles; afortunadamente, puede ser calculado directamente para cualquier distribución de probabilidad teórica. La Tabla 6.1 muestra la probabilidad acumulada de cada número posible de tiros libres exitosos del ejemplo de arriba, donde podemos ver que la probabilidad de que Curry anote 2 o menos tiros libres de un total de 4 intentos es 0.043.
| numSuccesses | Probability | CumulativeProbability |
|---|---|---|
| 0 | 0.000 | 0.000 |
| 1 | 0.003 | 0.003 |
| 2 | 0.040 | 0.043 |
| 3 | 0.271 | 0.314 |
| 4 | 0.686 | 1.000 |
6.4 Probabilidad condicional
Hasta ahora nos hemos limitado a probabilidades simples - esto es, la probabilidad de un solo evento o combinación de eventos. Sin embargo, frecuentemente deseamos determinar la probabilidad de algunos eventos dependiendo de que otro evento haya ocurrido, lo cual se conoce como probabilidad condicional.
Tomemos como ejemplo la elección Presidencial de EUA en 2016. Existen dos probabilidades simples que podríamos usar para describir al electorado. Primero, conocemos la probabilidad de que un votante en EUA esté afiliado al Partido Republicano: \(p(Republican) = 0.44\). También conocemos la probabilidad de que un votante dé su voto en favor de Donald Trump: \(p(Trump voter)=0.46\). Sin embargo, digamos que queremos saber lo siguiente: ¿Cuál es la probabilidad de que una persona vote por Donald Trump, dado que esa persona sea Republicana?
Para calcular la probabilidad condicional de A dado B (que escribimos como \(P(A|B)\), “probabilidad de A, dado B”), necesitamos conocer la probabilidad conjunta (esto es, la probabilidad de que ambos A y B ocurran) así como la probabilidad general de B:
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
Esto es, queremos saber la probabilidad de que ambas cosas sean ciertas, dado que aquella sobre la que está condicionada sea cierta.
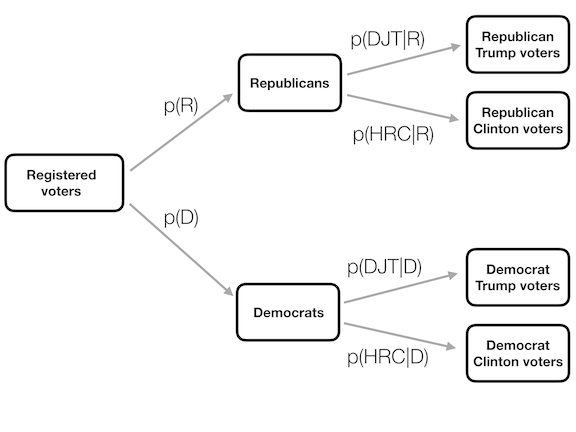
Figura 6.3: Representación gráfica de la probabilidad condicional, mostrando cómo la probabilidad condicional limita nuestro análisis a un subconjunto de los datos.
Puede ser útil pensar en esto gráficamente. La Figura 6.3 muestra un diagrama de flujo que representa cómo el total de la población de votantes se divide en Republicanos y Demócratas, y cómo la probabilidad condicional (condicinada sobre el partido) divide aún a los miembros de cada partido de acuerdo a su voto.
6.5 Calcular probabilidades condicionales a partir de los datos
También podemos calcular probabilidades condicionales desde los datos. Digamos que estamos interesades en la siguiente pregunta: ¿Cuál es la probabilidad de que alguien tenga diabetes, dado que no sea una persona físicamente activa? – esto es, \(P(diabetes|inactive)\). La base de datos NHANES incluye dos variables que abordan las dos partes de esta pregunta. La primera (Diabetes) pregunta si una persona ha sido enterada de que tenga diabetes, y la segunda (PhysActive) registra si una persona se involucra en deportes, fitness, o actividades recreativas que sean de al menos intensidad moderada. Primero calculemos las probabilidades simples, las cuales se muestran en la Tabla 6.2. La tabla muestra que la probabilidad de que una persona en la base de datos NHANES tenga diabetes es .1, y la probabilidad de que una persona sea inactivx es .45.
| Answer | N_diabetes | P_diabetes | N_PhysActive | P_PhysActive |
|---|---|---|---|---|
| No | 4893 | 0.9 | 2472 | 0.45 |
| Yes | 550 | 0.1 | 2971 | 0.55 |
| Diabetes | PhysActive | n | prob |
|---|---|---|---|
| No | No | 2123 | 0.39 |
| No | Yes | 2770 | 0.51 |
| Yes | No | 349 | 0.06 |
| Yes | Yes | 201 | 0.04 |
Para calcular \(P(diabetes|inactive)\) necesitaríamos también conocer la probabilidad conjunta de ser diabético y ser inactivo, además de las probabilidades simples de cada uno. Estas probabilidades se muestran en la Tabla 6.3.
Basados en estas probabilidades conjuntas, podemos calcular \(P(diabetes|inactive)\). Una manera de hacer esto en un programa de computadora es primero determinar si la variable PhysActive era igual a “No” en cada individuo, y luego obtener la media de esos valores. Debido a que los valores TRUE/FALSE son tratados como 1/0 respectivamente por la mayoría de los lenguajes de programación (incluidos R y Python), esto nos permite identificar fácilmente la probabilidad de un evento simple obteniendo simplemente la media de una variable lógica que representa si el valor era verdadero. Entonces usamos ese valor para calcular la probabilidad condicional, donde podemos encontrar la probabilidad de que alguien tenga diabetes dado que sea una persona físicamente inactiva es 0.141.
6.6 Independencia
El término “independiente” tiene un significado muy específico en estadística, que es un poco diferente del uso común del término. Independencia estadística entre dos variables significa que el conocer el valor de una variable no dice nada sobre el valor de la otra. Esto puede ser expresado como:
\[ P(A|B) = P(A) \]
Esto es, la probabilidad de A dado algún valor de B es la misma que la probabilidad general de A. Mirándolo de esta manera, podemos ver que muchos casos de lo que llamaríamos “independencia” en el mundo real no son realmente estadísticamente independientes. Por ejemplo, actualmente hay un movimiento de un pequeño grupo de ciudadanos de California que quiere declarar un nuevo estado independiente llamado Jefferson, que comprendería a un número de condados del norte de California y Oregon. Si esto pasara, entonces la probabilidad de que un residente actual de California ahora viviera en el estado de Jefferson sería \(P(\text{Jeffersonian})=0.014\), mientras que la probabilidad de que se mantuviera siendo un residente de California sería \(P(\text{Californian})=0.986\). Los nuevos estados serían políticamente independientes, pero no serían estadísticamente independientes, porque ¡si sabemos que una persona es Jeffersonian, entonces podemos estar segurxs de que no es Californian! Esto es, mientras que independencia en el lenguaje común frecuentemente se refiere a conjuntos que son excluyentes, independencia estadística se refiere al caso donde no se puede predecir nada sobre una variable del valor de otra variable. Por ejemplo, conocer el color de cabello de una persona es improbable que te diga algo sobre si la persona prefiere nieve de chocolate o fresa.
Revisemos otro ejemplo, usando la base de datos NHANES: ¿La salud mental y la salud física son independientes la una de la otra? NHANES incluye dos preguntas relevantes: PhysActive, que pregunta si un individuo es físicamente activo, y DaysMentHlthBad, que pregunta cuántos días en los últimos 30 días la persona ha experimentado malos días de salud mental. Consideremos a cualquiera que haya tenido más de 7 días de mala salud mental en el último mes como parte de un grupo con mala salud mental. Basados en esto, podemos definir una nueva variable llamada badMentalHealth como una variable lógica que nos diga si la persona ha tenido más de 7 días con mala salud mental o no. Primero podemos resumir estos datos para que muestren cuántas personas caen en cada combinación de las dos variables (mostradas en la Tabla 6.4), y luego dividir entre el total de observaciones para crear una tabla de proporciones (mostrada en la Tabla 6.5):
| PhysActive | Bad Mental Health | Good Mental Health | Total |
|---|---|---|---|
| No | 414 | 1664 | 2078 |
| Yes | 292 | 1926 | 2218 |
| Total | 706 | 3590 | 4296 |
| PhysActive | Bad Mental Health | Good Mental Health | Total |
|---|---|---|---|
| No | 0.10 | 0.39 | 0.48 |
| Yes | 0.07 | 0.45 | 0.52 |
| Total | 0.16 | 0.84 | 1.00 |
Esto nos muestra la proporción de todas las observaciones que caen en cada celda. Sin embargo, lo que queremos saber aquí es la probabilidad condicional de tener mala salud mental, dependiendo de si la persona es físicamente activa o no. Para calcular esto, dividimos cada grupo de actividad física sobre su número total de observaciones, de manera que cada renglón ahora suma uno (mostrado en la Tabla 6.6). Aquí vemos las probabilidades condicionales de tener mala o buena salud mental para cada grupo de actividad física (en las filas superiores) junto a la probabilidad general de tener buena o mala salud mental (en la tercera fila). Para determinar si la salud mental y la actividad física son independientes, compararíamos la probabilidad simple de tener mala salud mental (en la tercera fila) con la probabilidad condicional de tener mala salud mental dado que la persona sea físicamente activa (en la segunda fila).
| PhysActive | Bad Mental Health | Good Mental Health | Total |
|---|---|---|---|
| No | 0.20 | 0.80 | 1 |
| Yes | 0.13 | 0.87 | 1 |
| Total | 0.16 | 0.84 | 1 |
La probabilidad general de mala salud mental \(P(\text{bad mental health})\) es 0.16 mientras que la probabilidad condicional \(P(\text{bad mental health|physically active})\) es 0.13. Por lo tanto, parece ser que la probabilidad condicional es un poco menor que la probabilidad general, sugiriendo que no son independientes, aunque no podemos saber con certeza sólo observando estos números, porque estos números podrían ser diferentes debido a variabilidad aleatoria en nuestra muestra. Más tarde en el libro revisaremos herramientas estadísticas que nos permitirán probar de manera directa si estas variables son independientes.
6.7 Invertir una probabilidad condicional: regla de Bayes
En muchos casos, conocemos \(P(A|B)\) pero lo que realmente queremos conocer es \(P(B|A)\). Esto comúnmente ocurre en tamizajes (screenings) médicos, donde conocemos \(P(\text{resultado positivo en un test| enfermedad})\) pero lo que queremos conocer es \(P(\text{enfermedad|resultado positivo en un test})\). Por ejemplo, algunos doctores recomiendan que los hombres mayores a 50 años se sometan a un screening usando una prueba llamada antígeno prostático específico (APE) para detectar posible cáncer prostático. Antes de que una prueba sea aprobada para su uso la práctica médica, el fabricante debe probar dos aspectos del rendimiento de la prueba. Primero, deben mostrar qué tan sensible es – esto es, qué tan probable es que encuentre la enfermedad cuando está presente: \(\text{sensibilidad} = P(\text{prueba positiva| enfermedad})\). También deben mostrar qué tan específica es: esto es, qué tan probable es que dé un resultado negativo cuando no hay enfermedad presente: \(\text{especificidad} = P(\text{prueba negativa|no enfermedad})\). Para la prueba APE, sabemos que la sensibilidad es cercana al 80% y la especificidad es alrededor de 70%. Sin embargo, estos números no responden a la pregunta que el médico quiere responder acerca de un paciente en particular: ¿cuál es la probabilidad de que el paciente tenga cáncer realmente, dado que la prueba haya salido positiva? Esto requiere que se invierta la probabilidad condicional que define a la sensibilidad: en lugar de \(P(prueba\ positiva| enfermedad)\) nosotros queremos saber \(P(enfermedad|prueba\ positiva)\).
Para poder invertir la probabilidad condicional, podemos usar la regla de Bayes:
\[ P(B|A) = \frac{P(A|B)*P(B)}{P(A)} \]
La regla de Bayes es bastante sencilla de derivar, basados en las reglas de probabilidad que aprendimos previamente en este capítulo (ve el Apéndice para esta derivación).
Si sólo tenemos dos resultados, podemos expresar la regla de Bayes en una manera un poco más clara, usando la regla de la suma para redefinir \(P(A)\):
\[ P(A) = P(A|B)*P(B) + P(A|\neg B)*P(\neg B) \]
Usando esto, podemos redefinir la regla de Bayes:
\[ P(B|A) = \frac{P(A|B)*P(B)}{P(A|B)*P(B) + P(A|\neg B)*P(\neg B)} \]
Podemos alimentar estos números a la ecuación para determinar la probabilidad de que una persona con un resultado APE positivo realmente tenga cáncer – pero nota que para poder hacer esto, también necesitamos saber la probabilidad general de cáncer para esa persona, a la cual nos referimos frecuentemente como la tasa base. Tomemos el ejemplo de un hombre de 60 años, para el cual la probabilidad de cáncer de próstata en los siguientes 10 años es \(P(cancer)=0.058\). Usando los valores de sensibilidad y especificidad que mencionamos arriba, podemos calcular la probabilidad individual de tener cáncer dado un resultado positivo en la prueba:
\[ P(\text{cancer|test}) = \frac{P(\text{test|cancer})*P(\text{cancer})}{P(\text{test|cancer})*P(\text{cancer}) + P(\text{test|}\neg\text{cancer})*P(\neg\text{cancer})} \] \[ = \frac{0.8*0.058}{0.8*0.058 +0.3*0.942 } = 0.14 \] Eso es una probabilidad bastante baja – ¿lo encuentras sorpresivo? Para muchas personas lo es, y de hecho existe una sustancial literatura en psicología que muestra que las personas sistemáticamente ignoramos las tasas base (i.e. prevalencia general) en nuestros juicios.
6.8 Aprender de los datos
Otra manera de pensar la regla de Bayes es verla como una manera de actualizar nuestras creencias con base en los datos – esto es, aprender sobre el mundo usando datos. Veamos la regla de Bayes otra vez:
\[ P(B|A) = \frac{P(A|B)*P(B)}{P(A)} \]
Las diferentes partes de la regla de Bayes tienen nombres específicos, que se relacionan con su rol al usar la regla de Bayes para actualizar nuestras creencias. Comenzamos con una conjetura inicial acerca de la probabilidad de B (\(P(B)\)), al cual nos referimos como la probabilidad previa (prior probability). En el ejemplo de APE usamos la tasa base como nuestra probabilidad previa, porque era nuestra mejor conjetura sobre la probabilidad de cáncer en la persona antes de conocer los resultados de la prueba. Luego recolectamos datos, que en nuestro ejemplo era el resultado de la prueba. El grado en que la información A es consistente con el resultado B es dado por \(P(A|B)\), al cual nos referimos como probabilidad (likelihood). Puedes considerar ese valor como el qué tan probable es el dato, dado que la hipótesis particular que estamos probando fuera cierta. En nuestro ejemplo, la hipótesis que está siendo probada era si el individuo tenía cáncer, y la probabilidad estaba basada en nuestro conocimiento acerca de la sensibilidad de la prueba (esto es, la probabilidad de tener un resultado positivo en la prueba si la persona tuviera cáncer). El denominador (\(P(A)\)) es referido como la probabilidad marginal, porque expresa la probabilidad general del dato, promediado a lo largo de todos los valores posibles de B (que en nuestro ejemplo eran: enfermedad presente y enfermedad ausente). El resultado a la izquierda (\(P(B|A)\)) es referido como la probabilidad posterior - porque es lo que se obtiene después de hacer los cálculos.
Existe otra manera de escribir la regla de Bayes que hace esto un poco más claro:
\[ P(B|A) = \frac{P(A|B)}{P(A)}*P(B) \]
La parte del lado izquierdo (\(\frac{P(A|B)}{P(A)}\)) nos dice qué tanto es más probable o menos probable el dato A dado B, relativo a la probabilidad general (marginal) de los datos. Mientras que la parte del lado derecho (\(P(B)\)) nos dice qué tan probable nosotros pensábamos que era B antes de saber nada acerca del dato A. Esto hace más claro que el papel del teorema de Bayes es el actualizar nuestro conocimiento previo basado en el grado en que los datos son más probables dado B de lo que serían en general. Si la hipótesis es mucho más probable dado el dato que se obtuvo de lo que sería en general, entonces incrementamos nuestra creencia en la hipótesis; si es menos probable dado el dato que se obtuvo, entonces disminuimos nuestra creencia.
6.9 Posibilidades (odds) y razón de posibilidades (odds ratios)
El resultado de la sección anterior nos mostró que la probabilidad de que la persona tuviera cáncer basada en un resultado positivo de la prueba APE es aún bastante bajo, aunque es más que el doble de lo que pensábamos antes de conocer el resultado de la prueba. A veces nos gustaría cuantificar la relación entre probabilidades de manera más directa, lo cual podemos hacer al convertirlas en posibilidades (odds) que expresan la probabilidad relativa de que algo suceda o no suceda: \[ \text{odds of A} = \frac{P(A)}{P(\neg A)} \]
En nuestro ejemplo de APE, las posibilidades (odds) de tener cáncer (dada la prueba positiva) son:
\[ \text{odds of cancer} = \frac{P(\text{cancer})}{P(\neg \text{cancer})} =\frac{0.14}{1 - 0.14} = 0.16 \]
Esto nos dice que las posibilidades (odds) de tener cáncer son bastante bajas, aún incluso de que la prueba salió positiva. Para comparar, las posibilidades de obtener un 6 en un dado sencillo son:
\[ \text{odds of 6} = \frac{1}{5} = 0.2 \]
Como punto aparte, esta es la razón por la que muchos investigadores médicos se han vuelto crecientemente preocupados por el uso generalizado de pruebas de tamizaje para condiciones relativamente poco comunes; la mayoría de los resultados positivos terminarán siendo falsos positivos, resultando en pruebas de seguimiento innecesarias con posibles complicaciones, sin mencionar el estrés añadido al paciente.
También podemos usar posibilidades (odds) para comparar diferentes probabilidades, al calcular lo que es conocido como una razón de posibilidades (odds ratio) - que significa justamente eso. Por ejemplo, digamos que queremos saber qué tanto el resultado positivo en la prueba incrementa las posibilidades (odds) de un individuo de tener cáncer. Primero calculamos las posibilidades previas (prior odds) – esto es, las posibilidades antes de saber que la persona salió con un resultado positivo en la prueba. Estas son calculadas usando la tasa base (base rate):
\[ \text{prior odds} = \frac{P(\text{cancer})}{P(\neg \text{cancer})} =\frac{0.058}{1 - 0.058} = 0.061 \]
Luego podemos comparar estas con las posibilidades posteriores (posterior odds), que son calculadas usando la probabilidad posterior:
\[ \text{odds ratio} = \frac{\text{posterior odds}}{\text{prior odds}} = \frac{0.16}{0.061} = 2.62 \]
Esto nos dice que las posibilidades (odds) de tener cáncer se incrementan por 2.62 veces dado el resultado positivo en la prueba. Una razón de posibilidades (odds ratio) es un ejemplo de lo que después llamaremos un tamaño del efecto, que es una manera de cuantificar qué tan relativamente grande es un efecto estadístico en particular.
Nota de traducción: los odds ratio tienen muchas traducciones diferentes al español, lo que hace complicado explicarlos con un término que se use de manera generalizada en español. En México ha sido muy común llamarles razón de momios, pero momio es un término de lugares de apuestas que prácticamente sólo se usa en México. En esta traducción usamos la sugerencia de Tapia y Nieto (1993) en su artículo “Razón de posibilidades: una propuesta de traducción de la expresión odds ratio” publicado en la revista Salud Pública en México. Por lo que aquí tradujimos odds como posibilidades y odds ratio como razón de posibilidades.
6.10 ¿Qué significan las probabilidades?
Podría sorprenderte que es un poco extraño hablar acerca de la probabilidad de que una persona tenga cáncer dependiendo del resultado de una prueba; después de todo, la persona tiene o no tiene cáncer. Históricamente, han habido dos maneras diferentes en que se han interpretado las probabilidades. La primera (conocida como la interpretación frecuentista) interpreta las probabilidades en términos de frecuencias a largo plazo. Por ejemplo, en el caso del lanzamiento de moneda, reflejaría las frecuencias relativas de obtener cara en el largo plazo después de un gran número de lanzamientos. Mientras que esta interpretación puede hacer sentido para eventos que pueden ser repetidos muchas veces como un lanzamiento de moneda, hace menos sentido para eventos que sólo sucederán una vez, como la vida de una persona o una elección presidencial en particular; y como dijo famosamente el economista John Maynard Keynes, “En el largo plazo, todos estaremos muertos” (“In the long run, we are all dead”).
La otra interpretación de probabilidades (conocida como la interpretación Bayesiana) es como un grado de creencia en una proposición particular. Si yo te preguntara “¿Qué tan probable que los EUA regresarán a la Luna en 2040?” tú podrías dar una respuesta a esta pregunta basada en tu conocimiento y en tus creencias, aunque no haya ninguna frecuencia relevante para calcular una probabilidad frecuentista. Una manera en que frecuentemente encuadramos las probabilidades subjetivas es en términos de la disposición a aceptar una apuesta en particular. Por ejemplo, si tu crees que la probabilidad de que EUA llegue a la Luna en 2040 es 0.1 (i.e. posibilidades de 9 a 1), entonces eso significa que deberías estar dispuesto a aceptar una apuesta que pagara posibilidades de 9 a 1 o más si el evento sí ocurriera.
Como veremos, estas dos diferentes definiciones de probabilidad son muy relevantes para las dos maneras en que los estadísticos piensan sobre las pruebas de hipótesis estadísticas, que nos encontraremos en capítulos posteriores.
6.11 Objetivos de Aprendizaje
Habiendo leído este capítulo, deberías ser capaz de:
- Describir el espacio muestral para un experimento aleatorio seleccionado.
- Calcular la frecuencia relativa y probabilidad empírica para un conjunto de eventos dado.
- Calcular las probabilidades de eventos simples, eventos complementarios, y la unión e intersección de conjuntos de eventos.
- Describir la ley de números grandes.
- Describir la diferencia entre una probabilidad y una probabilidad condicional.
- Describir el concepto de independencia estadística.
- Usar el teorema de Bayes para calcular la probabilidad condicional inversa.
6.12 Lecturas sugeridas
- The Drunkard’s Walk: How Randomness Rules Our Lives, por Leonard Mlodinow.
- Ten Great Ideas about Chance, por Persi Diaconis y Brian Skyrms.
6.13 Apéndice
6.13.1 Derivación de la regla de Bayes
Primero, recuerda la regla para calcular una probabilidad condicional:
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
Podemos reordenar esto para obtener la fórmula para calcular la probabilidad conjunta usando la condicional:
\[ P(A \cap B) = P(A|B) * P(B) \]
Usando esto podemos calcular la probabilidad inversa:
\[ P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{P(A|B)*P(B)}{P(A)} \]