Capitulo 14 El Modelo Lineal General

Recuerda que previamente en este libro describimos el modelo básico en estadística:

\[ datos = modelo + error \] donde nuestro objetivo principal es encontrar el modelo que minimice el error, sujeto a otras restricciones (como el mantener el modelo relativamente simple para que podamos generalizar más allá de nuestros datos específicos). En este capítulo nos enfocaremos en una implementación particular de esta aproximación, que es conocido como el modelo lineal general (general linear model, o GLM). Ya has visto el modelo lineal general en el capítulo de Ajustar Modelos a los Datos, donde modelamos la altura de los datos de la base NHANES como una función de la edad; aquí proveeremos una introducción más general al concepto del GLM y de sus múltiples usos. Casi todos los modelos usados en estadística pueden ser planteados en términos del modelo lineal general o como una extensión de éste.

Antes de que discutamos el modelo lineal general, primero definamos dos conceptos que serán importantes para nuestra discusión:

• variable dependiente: Es la variable de los resultados que nuestro modelo busca explicar (usualmente referida como Y)
• variable independiente: Es la variable que queremos usar para poder explicar la variable dependiente (usualmente referida como X)

Puede haber múltiples variables dependientes, pero para este curso nos enfocaremos principalmente en situaciones donde sólo hay una variable dependiente en nuestro análisis.

Un modelo lineal general es uno en donde nuestro modelo para la variable dependiente está compuesto por una combinación lineal de variables independientes que cada una es multiplicada por un peso (el cual es frecuentemente referido con la letra griega beta - \(\beta\)), que determina la contribución relativa de esa variable independiente a la predicción del modelo.

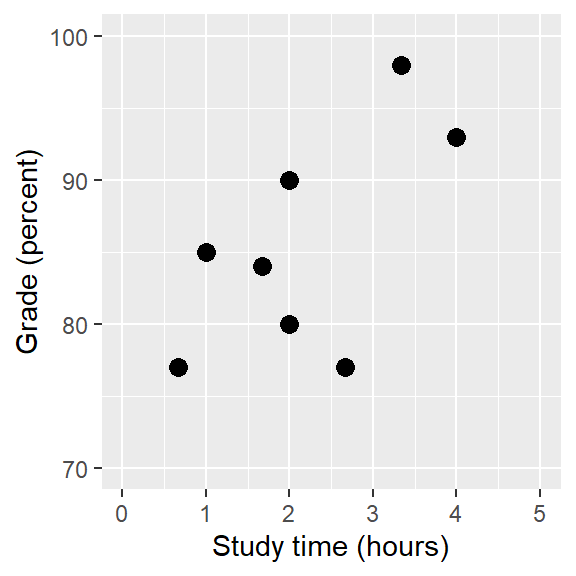
Figura 14.1: Relation between study time and grades

Como ejemplo, generemos unos datos simulados de la relación entre tiempo de estudio y calificación en exámenes (ve la Figura 14.1). Dados estos datos, quisiéramos hacer el ejercicio de desarrollar cada una de las tres actividades fundamentales de la Estadística:

• Describir: ¿Qué tan fuerte es la relación entre calificación y tiempo de estudio?
• Decidir: ¿Hay una relación estadísticamente significativa entre calificación y tiempo de estudio?
• Predecir: Dado un tiempo particular de estudio, ¿qué calificación esperaríamos?

En el capítulo anterior aprendimos cómo describir la relación entre dos variables usando el coeficiente de correlación. Usemos nuestro software estadístico para calcular esa relación para estos datos y hacer la prueba de si esa correlación es significativamente diferente de cero:

## 
##  Pearson's product-moment correlation
## 
## data:  df$grade and df$studyTime
## t = 2, df = 6, p-value = 0.09
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.13  0.93
## sample estimates:
##  cor 
## 0.63

Esta correlación es bastante alta, pero nota que el intervalo de confianza alrededor de nuestra estimación es bastante amplio, cubriendo casi todo el rango de valores desde cero a uno, que en parte se debe a que nuestro tamaño de muestra es pequeño.

14.1 Regresión lineal

Podemos usar el modelo lineal general para describir la relación entre dos variables y para decidir si la relación es estadísticamente significativa; además, el modelo nos permite predecir el valor de la variable dependiente dado algún o algunos valores nuevos de la(s) variable(s) independiente(s). Aún más importante, el modelo lineal general nos permite construir modelos que incorporen múltiples variables independientes, mientras que el coeficiente de correlación sólo puede describir la relación entre dos variables individuales.

La versión específica del GLM que usamos para esto es conocida como regresión lineal (linear regression). El término regresión fue acuñado por Francis Galton, quien notó que cuando él comparó padres y madres con sus hijxs en algunas características (como altura), lxs hijxs de padres y madres con valores extremos (i.e. lxs padres y madres muy altxs, o muy bajxs de estatura) generalmente caían más cerca de la media que de los valores de sus padres y madres. Este es un punto extremadamente importante al que regresaremos más abajo.

La versión más simple del modelo de regresión lineal (con una sola variable independiente) puede ser expresada de la siguiente manera:

\[ y = x * \beta_x + \beta_0 + \epsilon \] El valor \(\beta_x\) nos dice cuánto esperaríamos que \(y\) cambiara dado un cambio de una sola unidad en \(x\). El intercepto \(\beta_0\) es un offset general (una compensación general), que nos dice cuál valor esperaríamos de \(y\) cuando \(x=0\); recordarás de nuestra discusión previa sobre modelos que esto es importante para poder modelar la magnitud general de los datos, aún cuando \(x\) nunca tenga realmente un valor de cero. El término del error \(\epsilon\) se refiere al error que queda después de que el modelo ha sido ajustado a los datos; frecuentemente nos referimos a este error como los residuales del modelo. Si queremos saber cómo predecir \(y\) (que llamamos \(\hat{y}\)) después de estimar los valores \(\beta\), entonces podemos ignorar el término del error por el momento:

\[ \hat{y} = x * \hat{\beta_x} + \hat{\beta_0} \] Nota que esto es simplemente la ecuación de una línea, donde \(\hat{\beta_x}\) es nuestra estimación de la pendiente y \(\hat{\beta_0}\) es la constante. La Figura 14.2 muestra un ejemplo de este modelo aplicado a los datos de tiempo de estudio.

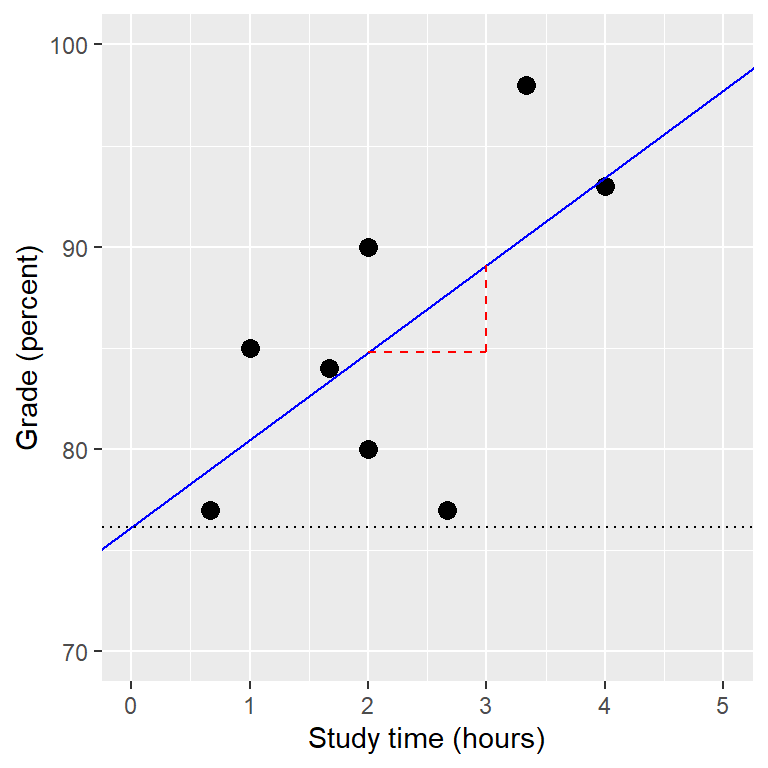
Figura 14.2: The linear regression solution for the study time data is shown in the solid line The value of the intercept is equivalent to the predicted value of the y variable when the x variable is equal to zero; this is shown with a dotted line. The value of beta is equal to the slope of the line – that is, how much y changes for a unit change in x. This is shown schematically in the dashed lines, which show the degree of increase in grade for a single unit increase in study time.

No entraremos en detalles sobre cómo se calcula la pendiente y el intercepto que mejor ajustan a los datos; si estás interesadx, los detalles están disponibles en el Apéndice.

14.1.1 Regresión a la media

El concepto de regresión a la media fue una de las contribuciones esenciales de Galton a la ciencia, y aún se mantiene como un punto crítico a entender cuando interpretamos los resultados de análisis de datos experimentales. Digamos que queremos estudiar los efectos de una intervención de lectura para el rendimiento de lectores de baja habilidad de lectura (“lectores pobres”). Para probar nuestra hipótesis, podríamos ir a una escuela y reclutar a aquellas personas en el 25% más bajo de la distribución en una prueba de lectura, administrar la intervención, y luego examinar su rendimiento en la prueba después de la intervención. Digamos que la intervención realmente no tiene efecto, de manera que los puntajes de lectura de cada persona son simplemente muestras independientes de una distribución normal. Los resultados de una simulación por computadora de este experimento hipotético se presentan en la Tabla 14.1.

Tabla 14.1: Puntajes de Lectura del Test 1 (que son menores, porque fueron la base para seleccionar a lxs estudiantes) y del Test 2 (que son mayores, porque no se relacionaban con el Test 1).

	Score
Test 1	88
Test 2	101

Si observamos la diferencia entre el rendimiento promedio en el primer y en el segundo test, pareciera que la intervención ha ayudado a estos estudiantes sustancialmente, ¡pues sus puntajes han incrementado en más de diez puntos en la prueba! Sin embargo, sabemos de cierto que estos estudiantes no mejoraron para nada, pues en ambos casos los puntajes simplemente fueron seleccionados de una distribución normal aleatoria. Lo que ha sucedido es que algunos estudiantes obtuvieron puntajes bajos en el primer test simplemente debido al azar. Si seleccionamos justo esos estudiantes con base en su puntaje del primer test, está garantizado que sus puntajes promedio se moverán hacia la media del grupo completo en su segundo test, aún cuando no hay ningún efecto del entrenamiento. Esta es una de las razones por las que siempre necesitamos un grupo control al que no se haya aplicado la intervención, para poder estar en posición de interpretar cualquier cambio en rendimiento como un cambio debido a la intervención; de otra manera probablemente seremos engañados por este truco de regresión a la media. Además, los participantes deben ser asignados aleatoriamente al grupo control o al experimental, para que no haya ninguna diferencia sistemática entre los grupos (en promedio).

14.1.2 La relación entre correlación y regresión

Hay una relación cercana entre los coeficientes de correlación y los coeficientes de regresión. Recuerda que el coeficiente de correlación de Pearson es calculado como la división de la covarianza entre la multiplicación de las desviaciones estándar de \(x\) y \(y\):

\[ \hat{r} = \frac{covariance_{xy}}{s_x * s_y} \] mientras que el coeficiente de regresión beta para x es calculado como:

\[ \hat{\beta_x} = \frac{covariance_{xy}}{s_x*s_x} \]

Basándonos en estas dos ecuaciones, podemos derivar la relación entre \(\hat{r}\) y \(\hat{beta}\):

\[ covariance_{xy} = \hat{r} * s_x * s_y \]

\[ \hat{\beta_x} = \frac{\hat{r} * s_x * s_y}{s_x * s_x} = r * \frac{s_y}{s_x} \] Esto es, la pendiente de la regresión es igual al valor de la correlación multiplicado por la división/proporción entre las desviaciones estándar de \(y\) y \(x\). Una cosa que nos dice esto es que cuando las desviaciones estándar de \(x\) y \(y\) son iguales (e.g. cuando los datos han sido convertidos a puntajes Z), entonces la correlación estimada es igual a la pendiente estimada de la regresión.

14.1.3 Errores estándar de los modelos de regresión

Si queremos realizar inferencias acerca de los parámetros estimados de regresión, entonces también necesitamos un estimado de su variabilidad. Para calcular esto, primero necesitamos calcular la varianza residual o varianza de error para el modelo – esto es, cuánta variabilidad en la variable dependiente no es explicada por el modelo. Podemos calcular los residuales del modelo de la manera siguiente:

\[ residual = y - \hat{y} = y - (x*\hat{\beta_x} + \hat{\beta_0}) \] Después calculamos la suma de errores cuadráticos (sum of squared errors, SSE):

\[ SS_{error} = \sum_{i=1}^n{(y_i - \hat{y_i})^2} = \sum_{i=1}^n{residuals^2} \] y de aquí podemos calcular la media del error cuadrático (mean squared error, MSE):

\[ MS_{error} = \frac{SS_{error}}{df} = \frac{\sum_{i=1}^n{(y_i - \hat{y_i})^2} }{N - p} \] donde los grados de libertad (\(gl\), degrees of freedom, \(df\)) se determinan al restar el número de parámetros estimados (2 en este caso: \(\hat{\beta_x}\) y \(\hat{\beta_0}\)) del número de observaciones (\(N\)). Una vez que tenemos la media del error cuadrático (MSE), podemos calcular el error estándar para el modelo de la siguiente manera:

\[ SE_{model} = \sqrt{MS_{error}} \]

Para poder obtener el error estándar para un parámetro estimado específico de la regresión, \(SE_{\beta_x}\), necesitamos reescalar el error estándar para el modelo mediante la raíz cuadrada de la suma de los cuadrados de la variable X:

\[ SE_{\hat{\beta}_x} = \frac{SE_{model}}{\sqrt{{\sum{(x_i - \bar{x})^2}}}} \]

14.1.4 Pruebas estadísticas para los parámetros de la regresión

Una vez que obtenemos los parámetros estimados y sus errores estándar, podemos calcular un estadístico t que nos diga la probabilidad (likelihood) del parámetro estimado observado comparado con algún valor esperado bajo la hipótesis nula. En este caso realizaremos la prueba contra la hipótesis nula de que no haya ningún efecto (i.e. \(\beta=0\)):

\[ \begin{array}{c} t_{N - p} = \frac{\hat{\beta} - \beta_{expected}}{SE_{\hat{\beta}}}\\ t_{N - p} = \frac{\hat{\beta} - 0}{SE_{\hat{\beta}}}\\ t_{N - p} = \frac{\hat{\beta} }{SE_{\hat{\beta}}} \end{array} \]

En general usaríamos un software estadístico para calcular estos valores en lugar de calcularlos a mano. Aquí están los resultados de la función del modelo lineal en R:

## 
## Call:
## lm(formula = grade ~ studyTime, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.656  -2.719   0.125   4.703   7.469 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    76.16       5.16   14.76  6.1e-06 ***
## studyTime       4.31       2.14    2.01    0.091 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.4 on 6 degrees of freedom
## Multiple R-squared:  0.403,  Adjusted R-squared:  0.304 
## F-statistic: 4.05 on 1 and 6 DF,  p-value: 0.0907

En este caso podemos ver que la constante es significativamente diferente de cero (lo cual no es muy interesante) y que el efecto de studyTime sobre las calificaciones es marginalmente significativo (p = .09) – el mismo valor p que el de la prueba de correlación que realizamos anteriormente.

14.1.5 Cuantificar la bondad de adjuste del modelo

Algunas veces es útil cuantificar qué tan bien ajusta el modelo a los datos en general, y una manera de hacer esto es preguntar cuánta de la variabilidad en los datos es explicada por el modelo. Esto es cuantificado usando un valor llamado \(R^2\) (también conocido como coeficiente de determinación, o coefficiente of determination en inglés). Si sólo hay una variable x, entonces este valor es fácil de calcular al simplemente elevar al cuadrado el coeficiente de correlación:

\[ R^2 = r^2 \] En el caso de nuestro ejemplo del tiempo de estudio, \(R^2\) = 0.4, que significa que hemos explicado cerca del 40% de la varianza en las calificaciones.

De manera más general, podemos pensar en \(R^2\) como una medida de la fracción de la varianza en nuestros datos que es explicada por el modelo, lo que puede ser calculado fraccionando la varianza en múltiples componentes:

\[ SS_{total} = SS_{model} + SS_{error} \] donde \(SS_{total}\) es la varianza de los datos (\(y\)) y \(SS_{model}\) y \(SS_{error}\) son calculadas como se vio previamente en este capítulo. Usando esto, podemos calcular el coeficiente de determinación como:

\[ R^2 = \frac{SS_{model}}{SS_{total}} = 1 - \frac{SS_{error}}{SS_{total}} \]

Un valor pequeño de \(R^2\) nos dice que aún cuando el ajuste del modelo sea estadísticamente significativo, estaría explicando sólo una pequeña cantidad de información en los datos.

14.2 Ajustar modelos más complejos

Frecuentemente nos gustaría entender los efectos de múltiples variables sobre un resultado en particular, y cómo se relacionan unas con otras. En el contexto de nuestro ejemplo del tiempo de estudio, digamos que descubrimos que algunos de los estudiantes habían tomado un curso previo sobre el tema. Si graficamos sus calificaciones (ve la Figura 14.3), podemos ver que aquellos que han tomado un curso previo obtuvieron un rendimiento más alto que aquellos que no, dado un mismo tiempo de estudio. Nos gustaría armar un modelo estadístico que tome eso en cuenta, lo cual podemos hacer expandiendo el modelo que construimos arriba:

\[ \hat{y} = \hat{\beta_1}*studyTime + \hat{\beta_2}*priorClass + \hat{\beta_0} \] Para modelar si cada persona había tomado un curso previo o no, usamos lo que se conoce como dummy coding (o codificación ficticia) en donde creamos una nueva variable que tiene el valor de uno para representar que se ha tomado una clase previa, y cero si no. Esto significa que para las personas que han tomado una clase previa, simplemente añadiremos el valor \(\hat{\beta_2}\) a nuestro valor predicho para ellos – esto es, el usar dummy coding \(\hat{\beta_2}\) simplemente refleja la diferencia en medias entre los dos grupos. Nuestra estimación de \(\hat{\beta_1}\) refleja la pendiente de regresión a lo largo de todos los datos – estamos asumiendo que la pendiente de regresión es la misma sin importar si las personas han tomado una clase previa o no (ve la Figura 14.3).

## 
## Call:
## lm(formula = grade ~ studyTime + priorClass, data = df)
## 
## Residuals:
##       1       2       3       4       5       6       7       8 
##  3.5833  0.7500 -3.5833 -0.0833  0.7500 -6.4167  2.0833  2.9167 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    70.08       3.77   18.60  8.3e-06 ***
## studyTime       5.00       1.37    3.66    0.015 *  
## priorClass1     9.17       2.88    3.18    0.024 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4 on 5 degrees of freedom
## Multiple R-squared:  0.803,  Adjusted R-squared:  0.724 
## F-statistic: 10.2 on 2 and 5 DF,  p-value: 0.0173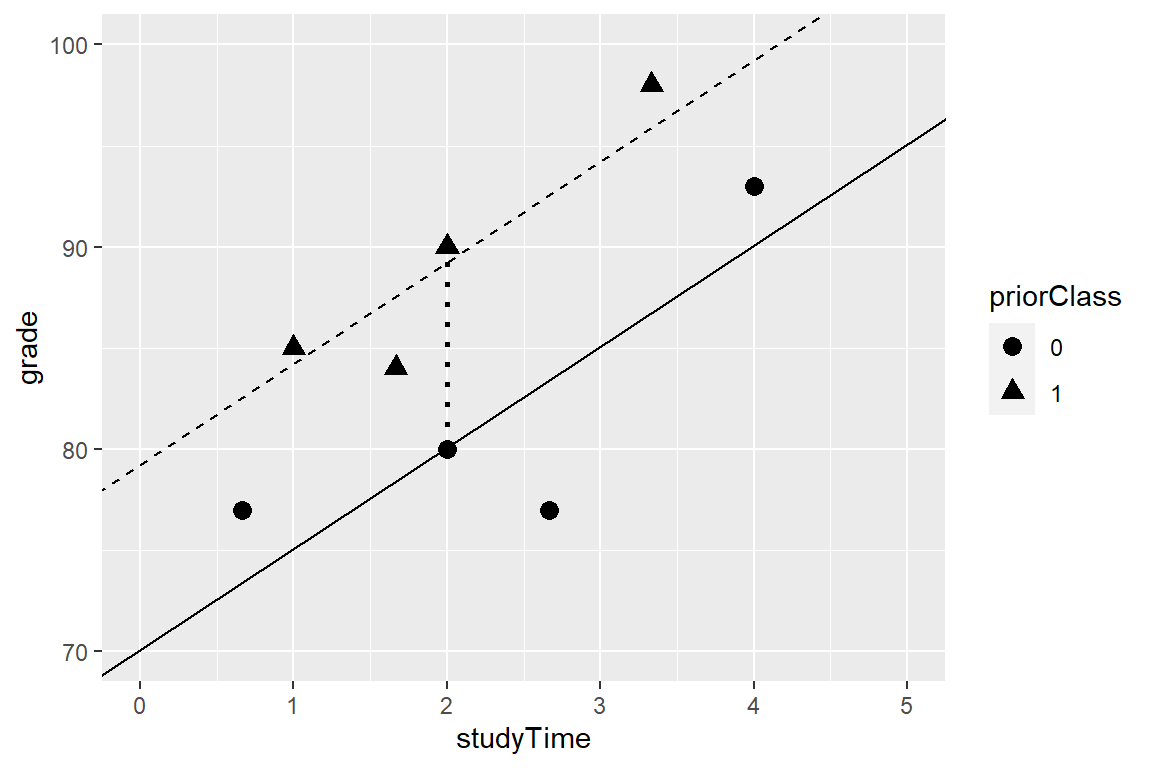

Figura 14.3: The relation between study time and grade including prior experience as an additional component in the model. The solid line relates study time to grades for students who have not had prior experience, and the dashed line relates grades to study time for students with prior experience. The dotted line corresponds to the difference in means between the two groups.

14.3 Interacciones entre variables

En el modelo anterior, asumimos que el efecto del tiempo de estudio sobre las calificaciones (i.e. la pendiente de la regresión) era el mismo para ambos grupos. Sin embargo, en algunos casos podríamos imaginar que el efecto de una variable podría diferir dependiendo del valor de alguna otra variable, a lo que llamamos una interacción (interaction) entre variables.

Usemos un nuevo ejemplo que haga la pregunta: ¿cuál es el efecto de la cafeína sobre el hablar en público? Primero generemos algunos datos y grafiquémoslos. Observando el panel A de la Figura 14.4, no parece haber una relación, y podemos confirmarlo realizando una regresión lineal sobre los datos:

## 
## Call:
## lm(formula = speaking ~ caffeine, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -33.10 -16.02   5.01  16.45  26.98 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)   -7.413      9.165   -0.81     0.43
## caffeine       0.168      0.151    1.11     0.28
## 
## Residual standard error: 19 on 18 degrees of freedom
## Multiple R-squared:  0.0642, Adjusted R-squared:  0.0122 
## F-statistic: 1.23 on 1 and 18 DF,  p-value: 0.281

Pero digamos que luego encontramos una investigación que sugiere que las personas ansiosas y las no ansiosas reaccionan diferente a la cafeína. Primero grafiquemos los datos separando a las personas ansiosas de las no ansiosas.

Como podemos ver en el panel B de la Figura 14.4, parece ser que la relación entre el hablar en público y la cafeína es diferente en los dos grupos, donde la cafeína mejora el rendimiento de las personas sin ansiedad y empeora el rendimiento de aquellas que tienen ansiedad. Queremos crear un modelo estadístico que resuelva esta pregunta. Primero veamos qué pasa si incluimos sólo ansiedad en el modelo.

## 
## Call:
## lm(formula = speaking ~ caffeine + anxiety, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -32.97  -9.74   1.35  10.53  25.36 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)
## (Intercept)        -12.581      9.197   -1.37     0.19
## caffeine             0.131      0.145    0.91     0.38
## anxietynotAnxious   14.233      8.232    1.73     0.10
## 
## Residual standard error: 18 on 17 degrees of freedom
## Multiple R-squared:  0.204,  Adjusted R-squared:  0.11 
## F-statistic: 2.18 on 2 and 17 DF,  p-value: 0.144

Aquí vemos que no hay efectos significativos de la cafeína ni de la ansiedad, lo que podría parecer un poco confuso. El problema es que este modelo está tratando de usar la misma pendiente al relacionar el hablar en público con la cafeína para ambos grupos. Si queremos ajustar los datos usando líneas con pendientes separadas, necesitamos incluir una interacción en el modelo, lo que es equivalente a ajustar diferentes líneas para cada uno de los dos grupos; esto es frecuentemente denotado usando el símbolo \(*\) en el modelo.

## 
## Call:
## lm(formula = speaking ~ caffeine + anxiety + caffeine * anxiety, 
##     data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.385  -7.103  -0.444   6.171  13.458 
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 17.4308     5.4301    3.21  0.00546 ** 
## caffeine                    -0.4742     0.0966   -4.91  0.00016 ***
## anxietynotAnxious          -43.4487     7.7914   -5.58  4.2e-05 ***
## caffeine:anxietynotAnxious   1.0839     0.1293    8.38  3.0e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.1 on 16 degrees of freedom
## Multiple R-squared:  0.852,  Adjusted R-squared:  0.825 
## F-statistic: 30.8 on 3 and 16 DF,  p-value: 7.01e-07

De estos resultados podemos ver que hay efectos significativos tanto de la cafeína como de la ansiedad (lo que llamamos efectos principales, o main effects) y también una interacción entre cafeína y ansiedad. El Panel C de la Figura 14.4 muestra las líneas de regresión separadas para cada grupo.

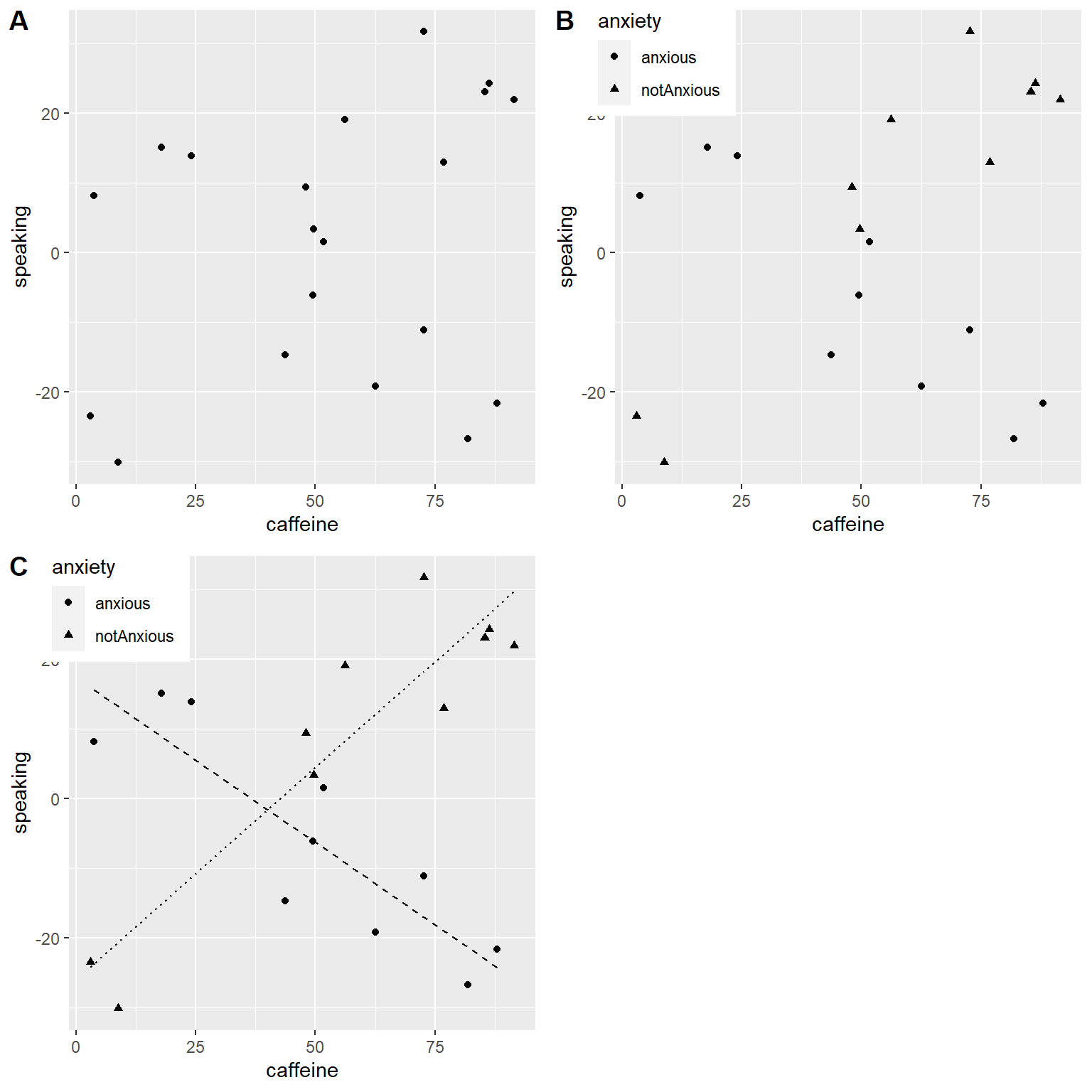
Figura 14.4: A: The relationship between caffeine and public speaking. B: The relationship between caffeine and public speaking, with anxiety represented by the shape of the data points. C: The relationship between public speaking and caffeine, including an interaction with anxiety. This results in two lines that separately model the slope for each group (dashed for anxious, dotted for non-anxious).

Un punto importante por resaltar es que debemos ser muy cuidadosxs al interpretar un efecto principal significativo si también está presente una interacción significativa, porque la interacción sugiere que el efecto principal difiere de acuerdo con los valores de otra variable, por lo que no es fácilmente interpretable.

Algunas veces queremos comparar el ajuste relativo de dos modelos diferentes, para poder determinar cuál modelo es mejor; llamamos a esto comparación de modelos (o model comparison). Para los modelos anteriores, podemos comparar la bondad de ajuste (goodness of fit) del modelo sin y con interacción, usando lo que se conoce como análisis de varianza (analysis of variance):

## Analysis of Variance Table
## 
## Model 1: speaking ~ caffeine + anxiety
## Model 2: speaking ~ caffeine + anxiety + caffeine * anxiety
##   Res.Df  RSS Df Sum of Sq    F Pr(>F)    
## 1     17 5639                             
## 2     16 1046  1      4593 70.3  3e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Esto nos indica que hay buena evidencia para preferir el modelo que incluye la interacción sobre el modelo que no la incluye. La comparación de modelos es relativamente simple en este caso porque los dos modelos están anidados (del inglés: nested) – uno de los modelos es una versión simplificada del otro modelo, de manera tal que todas las variables en el modelo simple están contenidas en el modelo más complejo. La comparación de modelos no-anidados se puede volver mucho más complicada.

14.4 Más allá de predictores y resultados lineales

Es importante hacer notar que a pesar del hecho de que se llame modelo lineal general, realmente podemos usar la misma maquinaria para modelar efectos que no siguen una línea recta (como las curvas). La palabra “lineal” en el modelo lineal general no se refiere a la forma de la respuesta, sino al hecho de que el modelo es lineal en sus parámetros – esto es, que los predictores en el modelo sólo pueden ser multiplicados por los parámetros, contrario a relaciones no lineales como el que fueran elevados a la potencia del parámetro. También es común analizar datos donde los resultados son binarios en lugar de continuos, como vimos en el capítulo sobre resultados categóricos. Existen formas de adaptar el modelo lineal general (conocidos como modelos lineales generalizados) que permiten este tipo de análisis. Exploraremos estos modelos después en este libro.

14.5 Criticar nuestro modelo y revisar suposiciones

El dicho “si metes basura, sacas basura” (“garbage in, garbage out”) es cierto para la estadística como en cualquier lugar. En el caso de modelos estadísticos, debemos asegurarnos de que nuestro modelo está especificado apropiadamente y que nuestros datos son apropiados para el modelo.

Cuando decimos que el modelo está “especificado apropiadamente,” queremos decir que hemos incluido el conjunto apropiado de variables independientes en el modelo. Ya hemos visto ejemplos de modelos mal especificados, en la Figura 5.3. Recuerda que vimos varios casos donde el modelo falló en explicar apropiadamente los datos, como cuando no se incluyó el intercepto. Cuando construimos un modelo, debemos asegurarnos que incluye todas las variables apropiadas.

También debemos preocuparnos si nuestro modelo satisface las suposiciones de nuestros métodos estadísticos. Una de las suposiciones más importantes que hacemos cuando usamos el modelo lineal general es que los residuales (esto es, la diferencia entre las predicciones de nuestro modelo y los datos verdaderos) están normalmente distribuidas. Esto puede fallar en cumplirse por varias razones, puede ser porque el modelo no estaba apropiadamente especificado, o porque los datos que estamos modelando son inapropiados.

Podemos usar algo conocido como una gráfica Q-Q (quantile-quantile, Q-Q plot) para ver si nuestros residuales están normalmente distribuidos. Ya te has encontrado con los cuantiles (quantiles) — son los valores que establecen un punto de corte para una proporción particular de una distribución acumulada. La gráfica Q-Q presenta los cuantiles de dos distribuciones una contra la otra; en este caso, presentaremos los cuantiles de los datos reales contra los cuantiles de una distribución normal ajustada a los mismos datos. La Figura 14.5 muestra ejemplos de dos gráficas Q-Q. El panel izquierdo muestra una gráfica Q-Q para datos de una distribución normal, mientras que el panel derecho muestra una gráfica Q-Q de una distribución no normal. Los datos en el panel derecho se desvían sustancialmente de la línea diagonal, reflejando el hecho de que no están normalmente distribuidos.

qq_df <- tibble(norm=rnorm(100),
                unif=runif(100))

p1 <- ggplot(qq_df,aes(sample=norm)) + 
  geom_qq() + 
  geom_qq_line() + 
  ggtitle('Normal data')

p2 <- ggplot(qq_df,aes(sample=unif)) + 
  geom_qq() + 
  geom_qq_line()+ 
  ggtitle('Non-normal data')

plot_grid(p1,p2)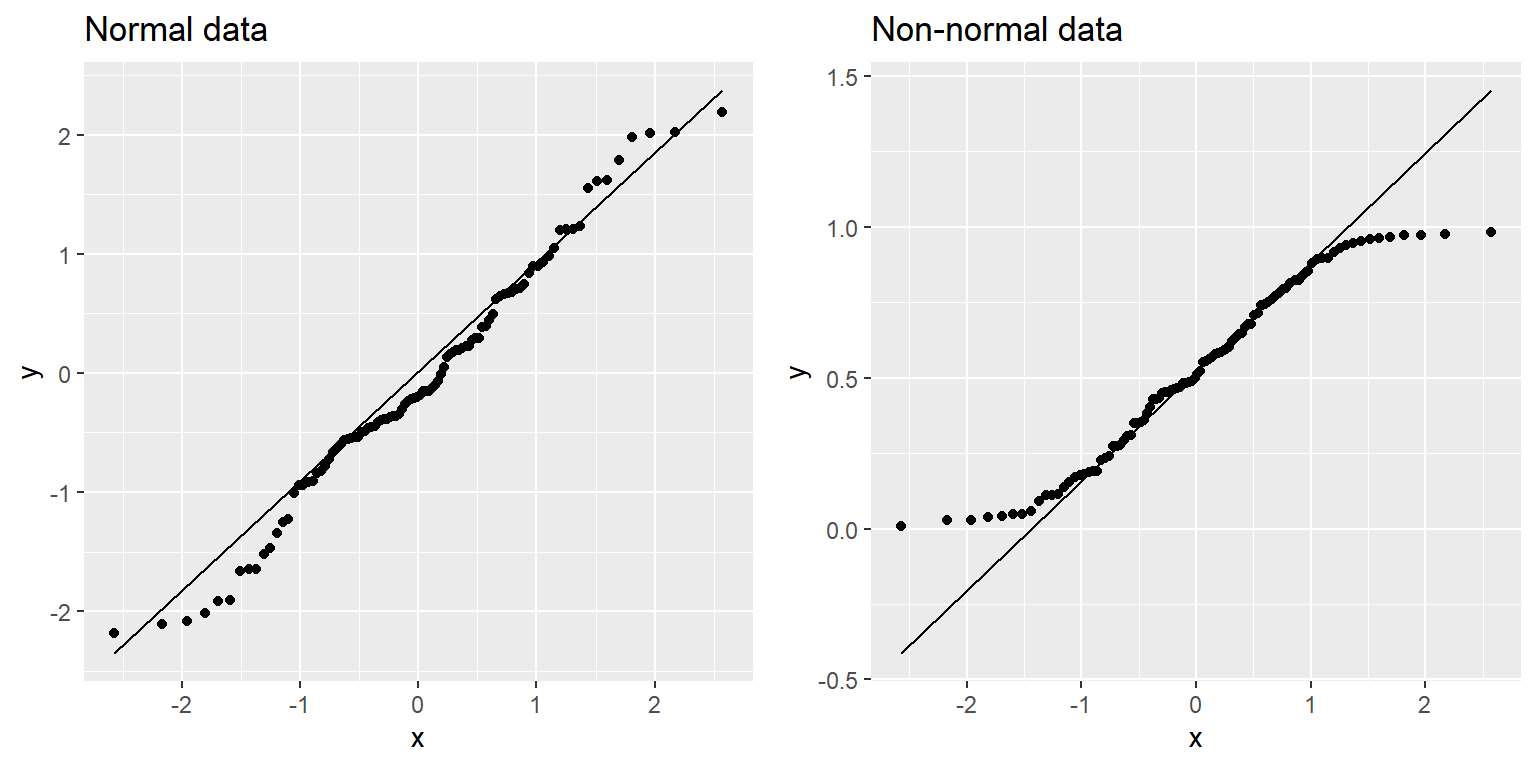

Figura 14.5: Q-Q plotsof normal (left) and non-normal (right) data. The line shows the point at which the x and y axes are equal.

Herramientas para el diagnóstico de modelos serán exploradas en mayor detalle en el capítulo siguiente.

14.6 ¿Qué significa realmente “predecir?”

Cuando hablamos de “predicción” en la vida diaria, generalmente nos referimos a la habilidad para estimar el valor de alguna variable antes de ver los datos. Sin embargo, el término frecuentemente es usado en el contexto de regresión lineal para referirse al ajuste de un modelo a los datos; los valores estimados (\(\hat{y}\)) en ocasiones son conocidos como “predicciones” y las variables independientes son conocidas como “preditores.” Esto tiene una connotación desafortunada, porque parece implicar que nuestro modelo debería ser capaz de predecir los valores de nuevos datos en el futuro. En realidad, el ajuste de un modelo al conjunto de datos usado para obtener sus parámetros casi siempre será mejor que el ajuste del mismo modelo a un nuevo conjunto de datos (Copas 1983).

Como ejemplo, tomemos una muestra de 48 niñxs de la base de datos NHANES y ajustemos un modelo de regresión para los datos de peso que incluya varios regresores (edad, altura, horas que pasan viendo TV y usando la computadora, e ingreso económico del hogar) junto con sus interacciones.

Tabla 14.2: Root mean squared error for model applied to original data and new data, and after shuffling the order of the y variable (in essence making the null hypothesis true)

Data type	RMSE (original data)	RMSE (new data)
True data	3.0	25
Shuffled data	7.8	59

Aquí podemos ver que mientras que el modelo mostró un ajuste muy bueno en los datos originales (sólo con error de algunos kg por persona), el mismo modelo hace un peor trabajo prediciendo los datos del peso de nuevos niñxs muestreados de la misma población (con error de más de 25 kg por persona). Esto sucede porque nuestro modelo especificado es bastante complejo, ya que incluye no sólo las variables individuales, sino también todas las posibles combinaciones entre ellas (i.e. sus interacciones), resultando en un modelo con 32 parámetros. Como esto significa tener casi tantos coeficientes como datos en la muestra (i.e., las alturas de 48 niñxs), el modelo se sobreajusta (overfits) a los datos, justo como sucedió con nuestra curva polinomial compleja en nuestro ejemplo inicial sobre el sobreajuste en la Sección 5.4.

Otra manera de ver los efectos del sobreajuste es el observar qué sucede si reordenamos aleatoriamente los valores de nuestra variable de peso (mostrada en la segunda fila de la tabla). El reordenar aleatoriamente los valores debería hacer imposible el predecir el peso a partir de otras variables, porque no tendrían ningún relación sistemática. Los resultados en la tabla muestran que incluso cuando no hay una verdadera relación a ser modelada (porque el reordenar aleatoriamente debería haber destruido cualquier relación), el modelo complejo aún muestra un error muy bajo en sus predicciones de los datos ajustados, porque termina ajustándose al error en nuestros datos específicos. Sin embargo, cuando el modelo es aplicado a nuevos datos, vemos que el error es mucho mayor, como debería suceder.

14.6.1 Validación cruzada (Cross-validation)

Un método que ha sido desarrollado para ayudar a resolver el problema del sobreajuste es conocido como validación cruzada (cross-validation). Esta técnica es comúnmente usada en el campo del aprendizaje máquina (machine learning), que está enfocado en construir modelos que puedan generalizarse bien a nuevos datos, incluso cuando no tenemos un nuevo conjunto de datos con el cual probar el modelo. La idea detrás de la validación cruzada es que ajustemos nuestro modelo repetidamente, cada vez dejando fuera un subconjunto de los datos, y luego probar la habilidad de nuestro modelo de predecir los valores en cada subconjunto de datos que se dejó fuera.

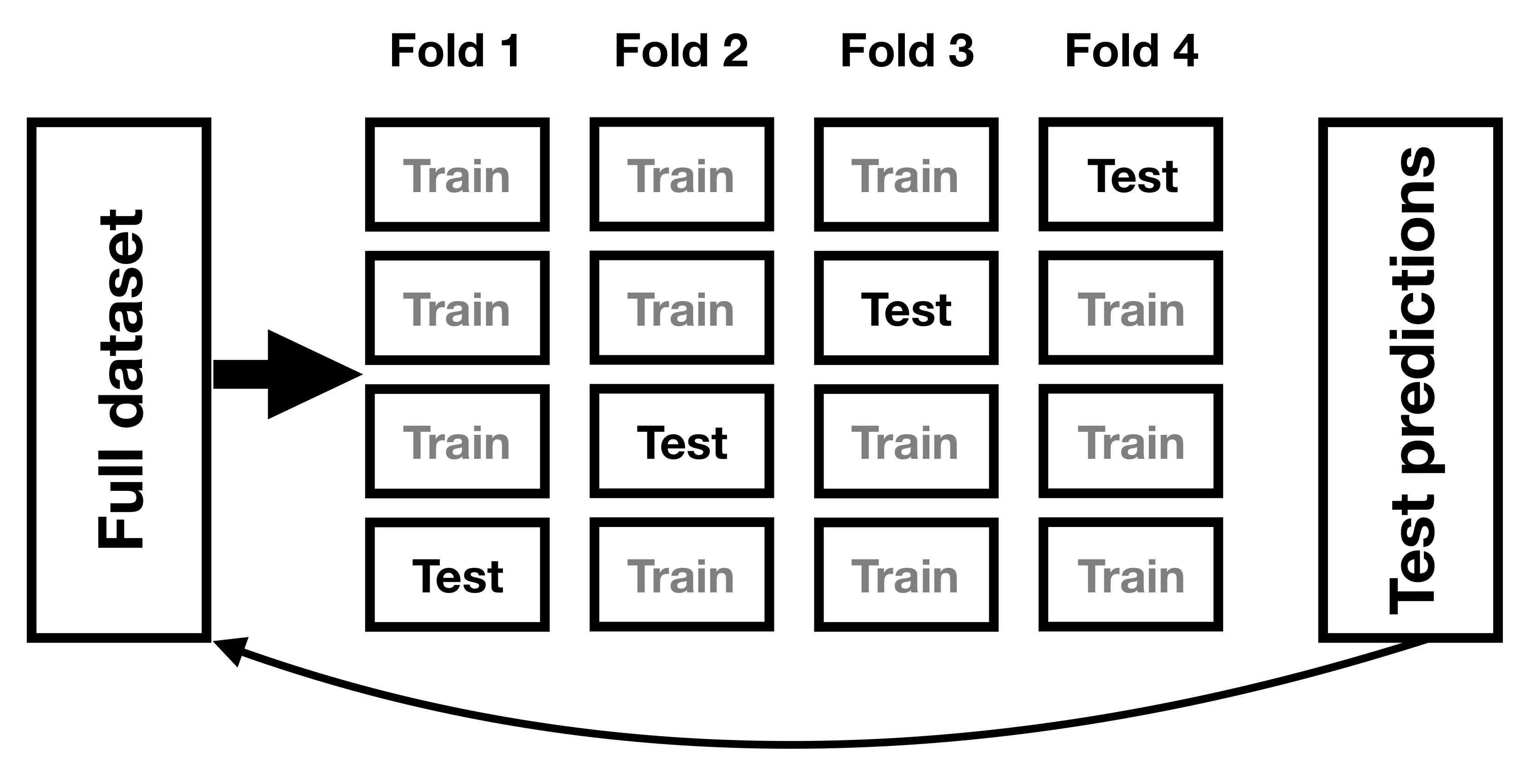
Figura 14.6: A schematic of the cross-validation procedure.

Veamos cómo funcionaría en nuestro ejemplo de predicción de pesos. En este caso realizaremos una validación cruzada con 12 subconjuntos (en inglés: 12-fold cross-validation), lo que significa que dividiremos nuestros datos en 12 subconjuntos, y luego ajustaremos el modelo 12 veces, en cada caso dejando fuera uno de los subconjuntos y luego probando la habilidad del modelo de poder predecir el valor de la variable dependiente para cada uno de los datos que se dejaron fuera. La mayoría de los softwares estadísticos provee herramientas para aplicar validación cruzada. Usando esta función podemos realizar una validación cruzada en 100 muestras de nuestros datos de NHANES, y calcular el RMSE para la validación cruzada, junto con el RMSE para los datos originales y para un nuevo conjunto de datos, como lo hicimos arriba.

Tabla 14.3: R-squared from cross-validation and new data, showing that cross-validation provides a reasonable estimate of the model’s performance on new data.

	R-squared
Original data	0.95
New data	0.34
Cross-validation	0.60

Aquí vemos que la validación cruzada nos da una estimación de la precisión predictiva que está mucho más cercana a lo que vemos con un conjunto de datos completamente nuevo, en lugar de la precisión inflada que vemos con los datos originales – de hecho, incluso es un poco más pesimista que el promedio para un nuevo conjunto de datos, probablemente porque sólo parte de los datos están siendo usados para entrenar cada uno de los modelos.

Nota que el usar la validación cruzada apropiadamente es complicado, y es recomendable que consultes con un experto antes de usarlo en la práctica. Sin embargo, esperemos que esta sección te haya mostrado tres cosas:

• “Predicción” no siempre significa lo que crees que significa.
• Modelos complejos pueden sobreajustarse a los datos pésimamente, a tal grado que unx podría aparentemente observar una buena predicción incluso cuando no hay una verdadera señal que predecir.
• Deberías de ver de manera muy escéptica afirmaciones acerca de la precisión de predicciones, a menos que hayan sido realizadas usando los métodos apropiados.

14.7 Objetivos de aprendizaje

Habiendo leído este capítulo, deberías ser capaz de:

• Describir el concepto de regresión lineal y aplicarlo a un conjunto de datos.
• Describir el concepto del modelo lineal general y proveer ejemplos de su aplicación.
• Describir cómo se utiliza la validación cruzada (cross-validation) para estimar el rendimiento predictivo de un modelo sobre nuevos datos.

14.8 Lecturas sugeridas

• The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd Edition) - The “bible” of machine learning methods, available freely online.

14.9 Apéndice

14.9.1 Estimar parámetros de una regresión lineal

Generalmente estimamos los parámetros de un modelo lineal a partir de los datos usando álgebra lineal, que es el tipo de álgebra que se aplica a vectores y matrices. Si no estás familiarizadx con el álgebra lineal, no te preocupes – pues realmente no la necesitaremos usar aquí, porque R (o el programa estadístico que uses) hará el trabajo por nosotrxs. Sin embargo, una breve excursión dentro del álgebra lineal nos puede proveer algún insight a cómo son estimados los parámetros de los modelos en la práctica.

Primero, presentemos la idea de vectores y matrices; ya los has encontrando en el contexto de R, pero los revisaremos aquí. Una matriz es un conjunto de números que están organizados en un cuadro o rectángulo, de manera que haya una o más dimensiones a lo largo de las cuales la matriz varía. La costumbre es colocar las diferentes unidades de observación (como las personas que observamos) en las filas, y diferentes variables en las columnas. Tomemos nuestro ejemplo de tiempo de estudio anterior. Podríamos organizar nuestros números en una matriz, que tendría ocho renglones o filas (una por cada estudiante) y dos columnas (una para tiempo de estudio, y otra para calificación). Si estás pensando “eso suena como un dataframe de R” (o de JASP) ¡estás totalmente en lo correcto! De hecho, un dataframe es una versión especializada de una matriz, y podemos convertir un dataframe a una matriz usando la función as.matrix().

df <-
  tibble(
    studyTime = c(2, 3, 5, 6, 6, 8, 10, 12) / 3,
    priorClass = c(0, 1, 1, 0, 1, 0, 1, 0)
  ) %>%
  mutate(
    grade = 
      studyTime * betas[1] + 
      priorClass * betas[2] + 
      round(rnorm(8, mean = 70, sd = 5))
  )

df_matrix <- 
  df %>%
  dplyr::select(studyTime, grade) %>%
  as.matrix()

Podemos escribir el modelo lineal general en álgebra lineal de la siguiente manera:

\[ Y = X*\beta + E \] Esto se parece mucho a la ecuación que usamos anteriormente, a excepción de que las letras están todas en mayúsculas, lo que quiere expresar el hecho de que son vectores.

Sabemos que los datos de las calificaciones van en la matriz \(Y\), pero ¿qué va en la matriz \(X\)? Recuerda de nuestra discusión inicial sobre la regresión lineal que necesitamos añadir una constante además de nuestra variable independiente de interés, por lo que nuestra matriz \(X\) (que llamamos matriz de diseño, o design matrix) necesita incluir dos columnas: una representando la variable tiempo de estudio, y una columna con el mismo valor para cada persona (que generalmente llenamos con números uno). Podemos ver la matriz de diseño resultante de manera gráfica (ve la Figura 14.7).

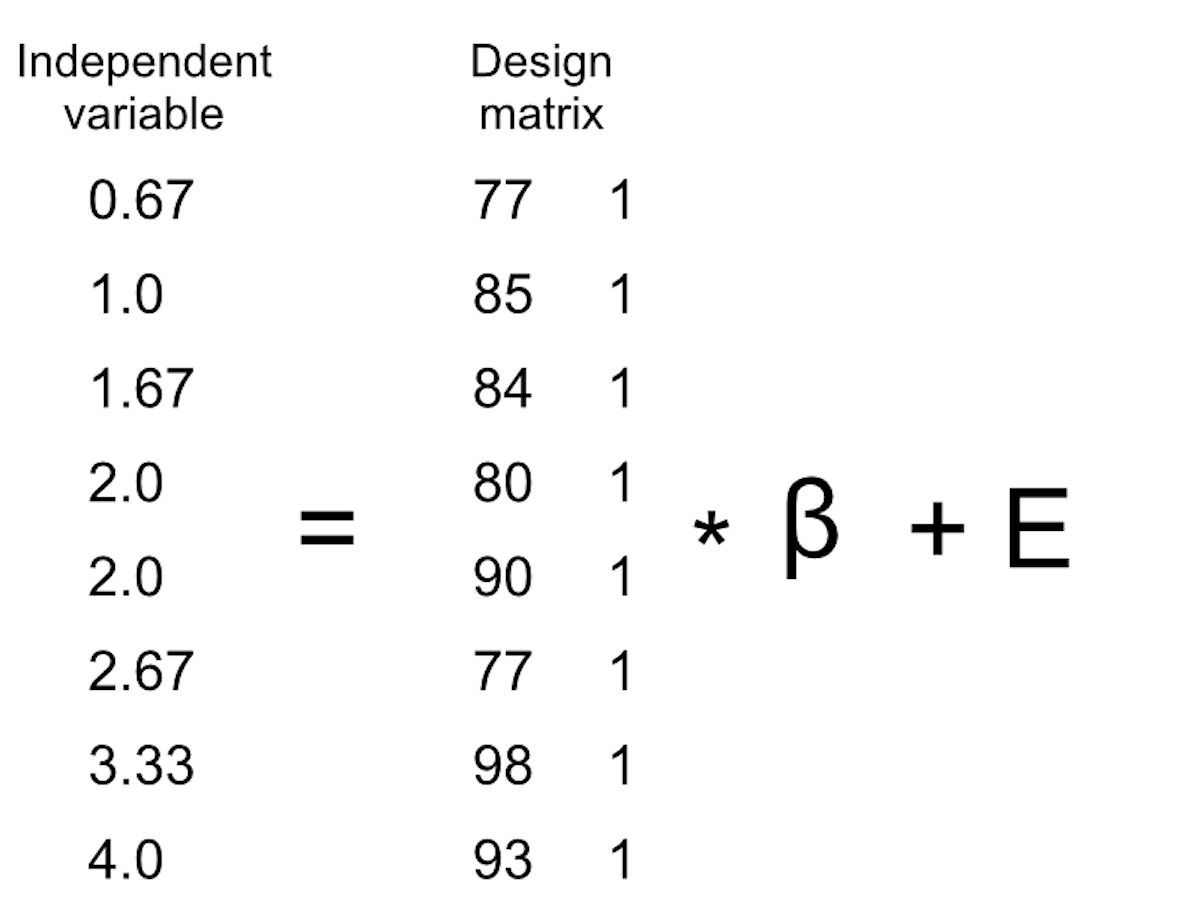
Figura 14.7: A depiction of the linear model for the study time data in terms of matrix algebra.

Las reglas de multiplicación de matrices nos dicen que las dimensiones de las matrices deben coincidir unas con otras; en este caso, la matriz de diseño tiene dimensiones de 8 (filas) X 2 (columnas) y la variable \(Y\) tiene dimensiones de 8 X 1. Entonces, la matriz \(\beta\) necesita tener dimensiones 2 X 1, porque una matriz 8 X 2 multiplicada por una matriz 2 X 1 resulta en una matriz 8 X 1 (pues las dimensiones de en medio que coinciden terminan desapareciendo). La interpretación de los dos valores en la matriz \(\beta\) es que son los valores por los cuales multiplicar el tiempo de estudio y el valor de 1 respectivamente para obtener la estimación de calificación para cada persona en la muestra. También podemos ver el modelo lineal como un conjunto de ecuaciones individuales para cada persona:

\(\hat{y}_1 = studyTime_1*\beta_1 + 1*\beta_2\)

\(\hat{y}_2 = studyTime_2*\beta_1 + 1*\beta_2\)

…

\(\hat{y}_8 = studyTime_8*\beta_1 + 1*\beta_2\)

Recuerda que nuestra meta es el determinar los valores \(\beta\) con mejor ajuste dado que conocemos los valores \(X\) y \(Y\). Una manera ingenua de hacer esto sería el resolver para \(\beta\) usando álgebra simple – aquí quitamos el término para el error \(E\) porque está fuera de nuestro control:

\[ \hat{\beta} = \frac{Y}{X} \]

El reto aquí está en que \(X\) y \(\beta\) son ahora matrices, no números sencillos – pero las reglas del álgebra lineal nos dicen cómo dividir entre una matriz, que es lo mismo que multiplicarla por el inverso de la matriz (referida como \(X^{-1}\)). Podemos hacer esto en R:

# compute beta estimates using linear algebra

#create Y variable 8 x 1 matrix
Y <- as.matrix(df$grade) 
 #create X variable 8 x 2 matrix
X <- matrix(0, nrow = 8, ncol = 2)
#assign studyTime values to first column in X matrix
X[, 1] <- as.matrix(df$studyTime) 
#assign constant of 1 to second column in X matrix
X[, 2] <- 1 

# compute inverse of X using ginv()
# %*% is the R matrix multiplication operator

beta_hat <- ginv(X) %*% Y #multiple the inverse of X by Y
print(beta_hat)

##      [,1]
## [1,]  8.2
## [2,] 68.0

Cualquier persona que esté interesada en un uso serio de métodos estadísticos se le recomienda fuertemente que invierta algún tiempo en aprender álgebra lineal, puesto que provee las bases para casi todas las herramientas que son usadas en estadística estándar.

Referencias

Copas, J. B. 1983. “Regression, Prediction and Shrinkage (with Discussion).” Journal of the Royal Statistical Society, Series B: Methodological 45: 311–54.