Capitulo 16 Modelación estadística práctica

En este capítulo reuniremos todo lo que hemos aprendido, aplicando nuestro conocimiento a un ejemplo práctico. En 2007, Christopher Gardner y colegas de Stanford publicaron un estudio en el Journal of the American Medical Association titulado “Comparison of the Atkins, Zone, Ornish, and LEARN Diets for Change in Weight and Related Risk Factors Among Overweight Premenopausal Women – The A TO Z Weight Loss Study: A Randomized Trial” (Gardner et al. 2007). Usaremos este estudio para mostrar cómo analizaríamos un conjunto de datos experimental de inicio a fin.

16.1 El proceso de modelación estadística

Hay un conjunto de pasos que generalmente seguimos cuando queremos usar nuestro modelo estadístico para probar hipótesis científicas:

  1. Especificar nuestra pregunta de interés.
  2. Identificar o recolectar los datos apropiados.
  3. Preparar los datos para el análisis.
  4. Determinar el modelo apropiado.
  5. Ajustar el modelo a los datos.
  6. Criticar el modelo para asegurarnos que se ajusta apropiadamente.
  7. Probar hipótesis y cuantificar el tamaño del efecto.

16.1.1 1: Especificar nuestra pregunta de interés.

De acuerdo a los autores, el objetivo de su estudio fue:

Comparar 4 dietas para perder peso que representan un espectro de ingesta de calorías de bajo a alto según sus efectos en la pérdida de peso y variables metabólicas relacionadas.

16.1.2 2: Identificar o recolectar los datos apropiados.

Para responder la pregunta, los investigadores asignaron aleatoriamente a 311 mujeres con sobrepeso u obesidad a una de cuatro diferentes dietas (Atkins, Zone, Ornish, o LEARN), y midieron su peso junto con otras variables de salud a lo largo del tiempo. Los autores registraron un gran número de variables, pero para la pregunta principal de interés nos enfocaremos en una variable sencilla: Índice de Masa Corporal (IMC; Body Mass Index, BMI). Además, como nuestra meta es medir cambios perdurables en IMC, revisaremos únicamente la medición tomada 12 meses después del inicio de la dieta.

16.1.3 3: Preparar los datos para el análisis.

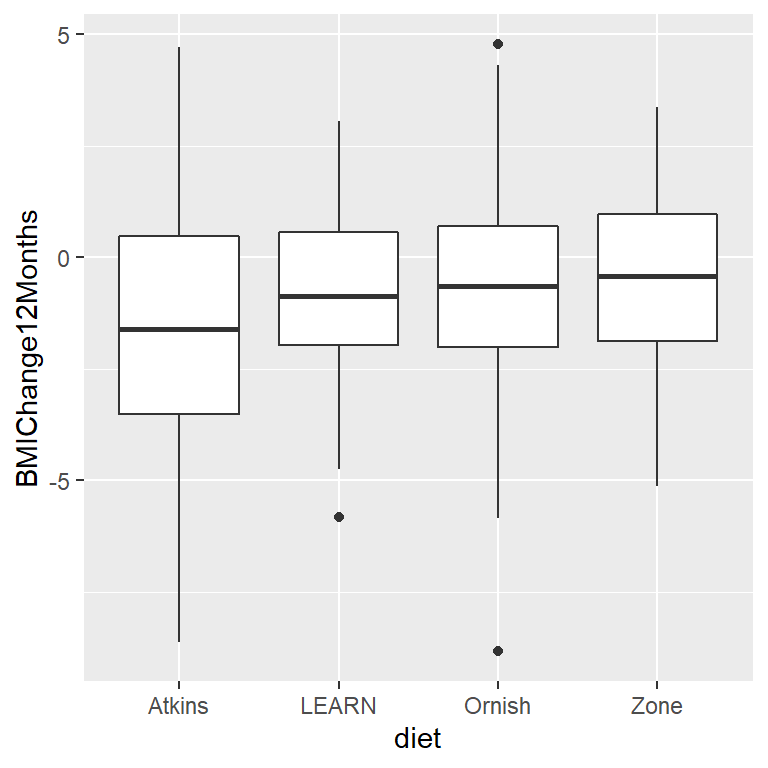
Boxplots para cada condición, con el percentil 50 (i.e. la mediana) mostrada con una línea negra para cada grupo.

Figura 16.1: Boxplots para cada condición, con el percentil 50 (i.e. la mediana) mostrada con una línea negra para cada grupo.

Los datos reales del estudio A a la Z no están disponibles públicamente, por lo que usaremos el resumen de los datos reportado en su artículo para generar datos sintéticos que aproximadamente coincidan con los datos obtenidos en su estudio, con las mismas medias y desviaciones estándar para cada grupo. Una vez que tenemos los datos, podemos visualizarlos para asegurarnos que no haya valores atípicos (outliers). Los diagramas de caja (boxplots) son útiles para ver la forma de la distribución, como se muestra en la Figura 16.1. Esos datos se ven bastante razonables - hay algunos outliers dentro de cada grupo individual (denotados por los puntos que quedan fuera de los boxplots), pero no se ve que sean extremos en comparación con los otros grupos. También podemos ver que las distribuciones parecen diferir un poco en sus varianzas, la dieta Atkins parece mostrar una variabilidad un poco mayor que las demás. Esto significa que cualquier análisis que asuma que las varianzas son iguales entre los grupos podría resultar inapropiado. Afortunadamente, el modelo ANOVA que planeamos usar es bastante robusto a esto.

16.1.4 4: Determinar el modelo apropiado.

Hay varias preguntas que necesitamos hacer para poder determinar el modelo estadístico apropiado para nuestro análisis.

  • ¿Qué tipo de variable dependiente?
    • IMC: continua, aproximadamente distribuida de manera normal.
  • ¿Qué estamos comparando?
    • Media de IMC de cuatro grupos de dieta.
    • ANOVA es apropiado.
  • ¿Las observaciones son independientes?
    • La asignación aleatoria debería asegurar que la suposición de independencia es apropiada.
    • El uso de puntuaciones de diferencias (en este caso la diferencia entre el peso inicial y el peso después de 12 meses) es algo controversial, especialmente cuando los puntos de inicio difieren entre los grupos. En este caso los puntos de inicio son muy similares entre los grupos, así que usaremos las puntuaciones de diferencias, pero en general uno querrá consultar a un estadístico antes de aplicar ese tipo de modelo a datos reales.

16.1.5 5: Ajustar el modelo a los datos.

Realicemos un ANOVA sobre los cambios en IMC para compararlo entre los cuatro tipos de dieta. La mayoría de los softwares estadísticos automáticamente convertirán una variable nominal en un conjunto de variables ficticias (dummy). Una manera común de especificar el modelo estadístico es usando la notación de fórmula, en la cual el modelo es especificado usando una fórmula con la estructura:

\[ \text{variable dependiente} \sim \text{variables independientes} \]

En este caso, queremos revisar los cambios en IMC (que están guardados en una variable llamada BMIChange12Months) como una función de la dieta (que está guardada en la variable llamada diet), así que usamos la siguiente fórmula:

\[ BMIChange12Months \sim diet \]

La mayoría del software estadístico (incluyendo R) automáticamente creará un conjunto de variables ficticias (dummy) cuando el modelo incluye una variable nominal (como la variable diet, que contiene el nombre de la dieta que cada persona recibió). Aquí están los resultados de este modelo ajustado a nuestros datos:

## 
## Call:
## lm(formula = BMIChange12Months ~ diet, data = dietDf)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -8.14  -1.37   0.07   1.50   6.33 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -1.622      0.251   -6.47  3.8e-10 ***
## dietLEARN      0.772      0.352    2.19   0.0292 *  
## dietOrnish     0.932      0.356    2.62   0.0092 ** 
## dietZone       1.050      0.352    2.98   0.0031 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.2 on 307 degrees of freedom
## Multiple R-squared:  0.0338, Adjusted R-squared:  0.0243 
## F-statistic: 3.58 on 3 and 307 DF,  p-value: 0.0143

Nota que el software estadístico automáticamente generó las variables ficticias (dummy variable) que corresponden a tres de las cuatro dietas, dejando la dieta Atkins sin una variable ficticia (dummy variable). Esto significa que la constante representa la media del grupo de la dieta Atkins, y las otras tres variables modelan la diferencia entre las medias de cada una de las dietas y la media de la dieta Atkins. Atkins fue elegida como la variable de línea base sin modelar simplemente porque es la primera en orden alfabético.

16.1.6 6: Criticar el modelo para asegurarnos que se ajusta apropiadamente.

La primera cosa que queremos hacer es criticar el modelo para asegurarnos que es apropiado. Una cosa que podemos hacer es ver los residuales del modelo. En la Figura 16.2, graficamos los residuales para cada persona agrupados según la dieta. No hay diferencias obvias en las distribuciones de los residuales entre las condiciones, podemos seguir adelante con el análisis.

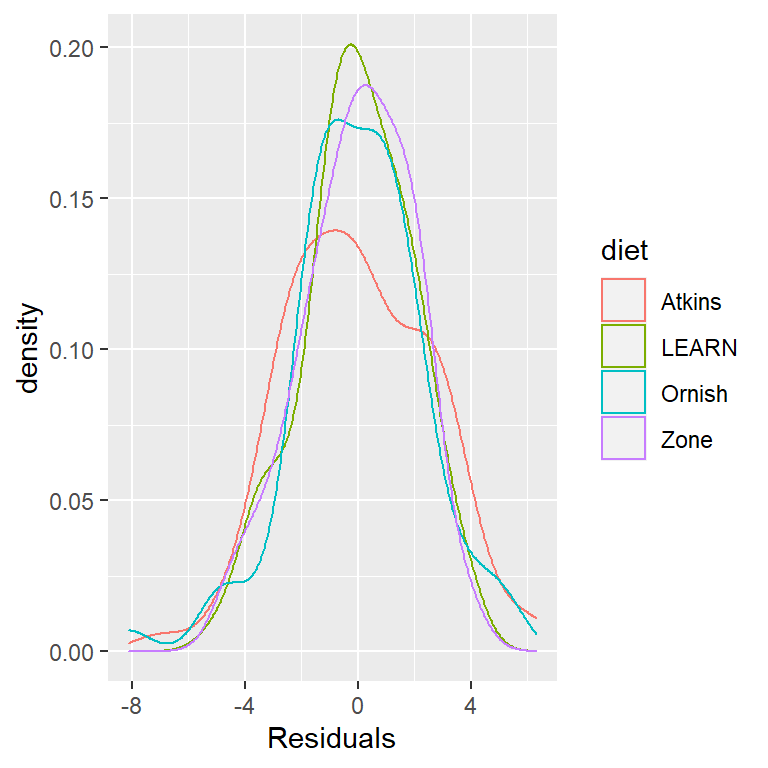
Distribución de residuales para cada condición.

Figura 16.2: Distribución de residuales para cada condición.

Otra suposición importante de las pruebas estadísticas que aplicamos a modelos lineales es que los residuales del modelo estén normalmente distribuidos. Es una idea equivocada algo común pensar que los modelos lineales requieren que los datos estén distribuidos de manera normal, pero esto no es correcto; el único requisito para que las estadísticas estén correctas es que los errores residuales estén normalmente distribuidos. El panel derecho de la Figura 16.3 muestra una gráfica Q-Q (quantile-quantile, cuantil-cuantil) que grafica los residuales contra su valor esperado basado en sus cuantiles en la distribución normal. Si los residuales están normalmente distribuidos entonces los datos caerían a lo largo de la línea punteada — en este caso se ven bastante bien, excepto por un par de valores atípicos (outliers) que son evidentes hasta abajo. Debido a que este modelo es también relativamente robusto a desviaciones de la normalidad, y a que éstas son relativamente pequeñas, seguiremos adelante y usaremos estos resultados.

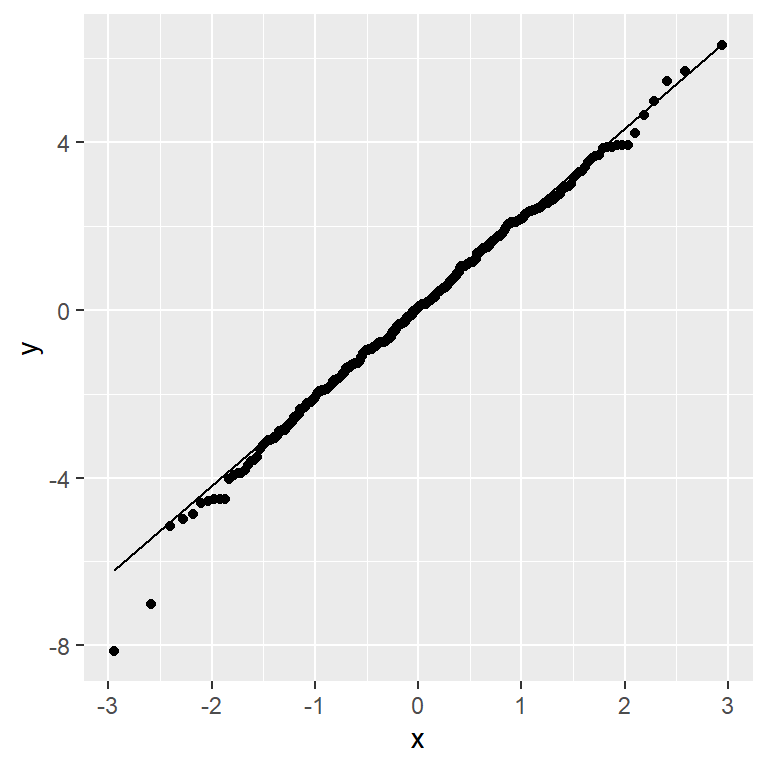
Gráfica Q-Q de los valores residuales reales contra sus valores residuales teóricos.

Figura 16.3: Gráfica Q-Q de los valores residuales reales contra sus valores residuales teóricos.

16.1.7 7: Probar hipótesis y cuantificar el tamaño del efecto.

Primero, veamos de nuevo el resumen de resultados del ANOVA, mostrado en el Paso 5 arriba. La prueba F significativa nos muestra que existe una diferencia significativa entre las dietas, pero deberíamos notar también que el modelo realmente no explica mucha varianza en los datos; el valor de R-cuadrada (R-squared) es sólo 0.03, mostrando que el modelo sólo explica muy poco porcentaje de la varianza en la pérdida de peso. Por lo tanto, no querremos sobre-interpretar este resultado.

El resultado significativo en la prueba F omnibus tampoco nos dice cuáles dietas difieren de cuáles otras. Podemos averiguar más si comparamos las medias entre condiciones. Como estaríamos haciendo varias comparaciones, necesitamos aplicar una corrección por esas comparaciones múltiples, esto se puede lograr usando un procedimiento conocido como método Tukey, que se puede calcular con nuestro software estadístico:

##  diet   emmean    SE  df lower.CL upper.CL .group
##  Atkins  -1.62 0.251 307    -2.11    -1.13  a    
##  LEARN   -0.85 0.247 307    -1.34    -0.36  ab   
##  Ornish  -0.69 0.252 307    -1.19    -0.19   b   
##  Zone    -0.57 0.247 307    -1.06    -0.08   b   
## 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 4 estimates 
## significance level used: alpha = 0.05 
## NOTE: Compact letter displays can be misleading
##       because they show NON-findings rather than findings.
##       Consider using 'pairs()', 'pwpp()', or 'pwpm()' instead.

Las letras en la columna hasta la derecha nos muestran cuáles de los grupos difieren de los otros, usando un método que ajusta por el número de comparaciones siendo realizadas; las condiciones que comparten una letra no son significativamente diferentes entre ellas. Esto nos muestra que las dietas Atkins y LEARN no difieren entre sí (porque comparten la letra a), y las dietas LEARN, Ornish, y Zone no difieren entre sí (porque comparten la letra b), pero la dieta Atkins difiere de las dietas Ornish y Zone (porque no comparten letras).

16.1.8 ¿Qué pasa con los posibles factores de confusión (confounds)?

Si vemos más de cerca el artículo de Gardner, veremos que también reportaron estadísticas sobre cuántas personas en cada grupo habían sido diagnosticadas con síndrome metabólico, que es un síndrome caracterizado por presión sanguínea alta, alta glucosa en sangre, exceso de grasa corporal alrededor de la cintura, y niveles de colesterol anormales; este síndrome está asociado con mayor riesgo de problemas cardiovasculares. Los datos del artículo de Gardner se presentan en la Tabla 16.1.

Tabla 16.1: Presencia de síndrome metabólico en cada grupo del estudio AtoZ.
Diet N P(metabolic syndrome)
Atkins 77 0.29
LEARN 79 0.25
Ornish 76 0.38
Zone 79 0.34

Mirando estos datos parece que las proporciones son ligeramente distintas entre los grupos, con más casos de síndrome metabólico en las dietas Ornish y Zone – que fueron justamente las dietas con peores resultados. Digamos que estamos interesados en probar si la proporción de personas con síndrome metabólico fue significativamente diferente entre los grupos, porque esto nos podría llevar a preocuparnos de que estas diferencias hayan podido haber afectado los resultados de las dietas.

16.1.8.1 Determinar el modelo apropiado

  • ¿Qué tipo de variable dependiente?
    • proporciones
  • ¿Qué estamos comparando?
    • proporción de síndrome metabólico en los cuatro grupos de dieta
    • prueba ji-cuadrada de bondad de ajuste (goodness of fit) es apropiada contra la hipótesis nula de no diferencia

Primero calculemos el estadístico, usando una función de la prueba ji-cuadrada en nuestro software estadístico:

## 
##  Pearson's Chi-squared test
## 
## data:  contTable
## X-squared = 4, df = 3, p-value = 0.3

Esta prueba muestra que no hay una diferencia significativa entre los grupos. Sin embargo, no nos dice qué tan seguros estamos de que no haya una diferencia; recuerda que bajo la NHST, siempre estamos trabajando bajo la suposición de que la nula es verdadera a menos que los datos nos muestren suficiente evidencia que nos lleve a rechazar la hipótesis nula.

¿Qué pasa si queremos cuantificar la evidencia a favor o en contra de la nula? Podemos hacer esto usando el factor de Bayes.

## Bayes factor analysis
## --------------
## [1] Non-indep. (a=1) : 0.058 ±0%
## 
## Against denominator:
##   Null, independence, a = 1 
## ---
## Bayes factor type: BFcontingencyTable, independent multinomial

Esto nos muestra que la hipótesis alternativa es 0.058 veces más probable que la hipótesis nula, que significa que la hipótesis nula es 1/0.058 ~ 17 veces más probable que la hipótesis alternativa dados estos datos. Esto es evidencia bastante fuerte, si no abrumadoramente fuerte, en favor de la hipótesis nula.

16.2 Obtener ayuda

Siempre que uno analiza datos reales, es útil verificar nuestro plan de análisis con una persona entrenada en estadística, porque hay muchos problemas potenciales que podrían surgir en datos reales. De hecho, es mucho mejor hablar con un estadísticx antes de siquiera comenzar el proyecto, pues su asesoría acerca del diseño o implementación del estudio podrían salvarte de grandes dolores de cabeza posteriormente. La mayoría de las universidades tienen oficinas o departamentos de consultoría estadística que ofrecen asistencia gratuita a los miembros de la comunidad universitaria. Entender el contenido de este libro no evitará que necesites su ayuda en algún punto, pero sí te ayudará a tener una conversación más informada con ese departamento y a entender mejor la asesoría que puedan ofrecerte.

Referencias

Gardner, Christopher D, Alexandre Kiazand, Sofiya Alhassan, Soowon Kim, Randall S Stafford, Raymond R Balise, Helena C Kraemer, and Abby C King. 2007. “Comparison of the Atkins, Zone, Ornish, and LEARN Diets for Change in Weight and Related Risk Factors Among Overweight Premenopausal Women: The a TO z Weight Loss Study: A Randomized Trial.” JAMA 297 (9): 969–77. https://doi.org/10.1001/jama.297.9.969.