Capitulo 9 Prueba de hipótesis

En el primer capítulo discutimos los tres grandes objetivos de la estadística:

• Describir
• Decidir
• Predecir

En este capítulo presentaremos las ideas detrás del uso de la estadística para tomar decisiones – en particular, decisiones acerca de si una hipótesis en particular es apoyada por los datos.

9.1 Prueba Estadística de Hipótesis Nula (Null Hypothesis Statistical Testing, NHST)

El tipo específico de prueba de hipótesis que discutiremos es conocido (por razones que serán claras más adelante) como prueba estadística de hipótesis nula (null hypothesis statistical testing, NHST). Si tomaras casi cualquier publicación científica o biomédica, verías la NHST siendo usada para probar hipótesis, y en su libro de texto de introducción a la psicología, Gerrig & Zimbardo (2002) se refirieron a la NHST como el “pilar de la investigación psicológica.” Por lo tanto, aprender cómo usar e interpretar los resultados de la prueba de hipótesis es esencial para entender los resultados de muchos campos de investigación.

También es importante que sepas, sin embargo, que la NHST tiene serias fallas, y muchos estadísticos e investigadores (incluyéndome) piensan que esto ha sido la causa de problemas serios en la ciencia, que discutiremos en el Capítulo 17. Por más de 50 años, ha habido llamados para abandonar la NHST en favor de otras aproximaciones (como aquellas que discutiremos en los siguientes capítulos):

• “La prueba de significatividad estadística en la investigación psicológica podría considerarse como un ejemplo de un tipo de sinsentido fundamental en el desarrollo de la investigación” [“The test of statistical significance in psychological research may be taken as an instance of a kind of essential mindlessness in the conduct of research”] (Bakan, 1966)
• La prueba de hipótesis es “una visión errada acerca de lo que constituye el progreso científico” [Hypothesis testing is “a wrongheaded view about what constitutes scientific progress”] (Luce, 1988)

NHST también es ampliamente malentendida, en gran medida porque va contra nuestras intuiciones acerca de cómo debería funcionar una prueba estadística de hipótesis. Veamos un ejemplo para observar esto.

9.2 Prueba estadística de hipótesis nula: Un ejemplo

Hay un gran interés en el uso de cámaras llevadas en el cuerpo por oficiales de policía, que se piensa que reducen el uso de la fuerza y mejoran el comportamiento del oficial. Sin embargo, para poder establecer esto necesitamos evidencia experimental, y se ha vuelto cada vez más común que los gobiernos usen ensayos controlados aleatorizados (randomized control trials) para probar este tipo de ideas. Un ensayo controlado aleatorizado de la efectividad del uso de cámaras en el cuerpo fue realizado por el gobierno de Washington, DC, y el DC Metropolitan Police Department en 2015/2016. Los oficiales fueron asignados de manera aleatoria a usar cámaras en el cuerpo o no, y su comportamiento fue seguido por un tiempo para determinar si las cámaras resultaron en menor uso de la fuerza y menos quejas de civiles acerca del comportamiento del oficial.

Antes de que lleguemos a los resultados, preguntémonos cómo piensas que el análisis estadístico debería funcionar. Digamos que queremos específicamente probar la hipótesis de si el uso de la fuerza disminuye por el uso de las cámaras. El ensayo controlado aleatorizado nos provee con los datos para probar la hipótesis – concretamente, la frecuencia de uso de la fuerza por oficiales asignados ya sea al grupo de cámara o al grupo control. El siguiente paso obvio es mirar los datos y determinar si proveen evidencia convincente a favor o en contra de esta hipótesis. Esto es: ¿Cuál es la probabilidad de que las cámaras usadas en el cuerpo reduzcan el uso de la fuerza, dados los datos y todo lo demás que sabemos?

Resulta que esta no es la manera en que funciona la prueba de hipótesis nula. En su lugar, primero tomamos nuestra hipótesis de interés (i.e. que las cámaras usadas en el cuerpo reducen el uso de la fuerza), y la volteamos de cabeza, creando una hipótesis nula – en este caso, la hipótesis nula sería que las cámaras no reducen el uso de la fuerza. De manera importante, luego de esto asumimos que la hipótesis nula es verdadera. Después miramos los datos, y determinamos qué tan probable serían estos datos si la hipótesis nula fuera cierta. Si los datos son los suficientemente improbables bajo la hipótesis nula, entonces podemos rechazar la nula en favor de la hipótesis alternativa que es nuestra hipótesis de interés. Si no hay suficiente evidencia para rechazar la nula, entonces decimos que conservamos (o “fallamos en rechazar”) la nula, quedándonos con nuestra suposición inicial de que la nula es cierta.

El entender algunos de los conceptos de NHST, particularmente el notable “valor p,” es invariablemente desafiante la primera vez que uno se encuentra con ellos, porque son tan contra-intuitivos. Como veremos después, existen otras aproximaciones que proveen maneras más intuitivas para abordar la prueba de hipótesis (pero tienen sus propias complejidades). Sin embargo, antes de que lleguemos a esas, es importante que tengas una comprensión profunda de cómo funciona la prueba de hipótesis, porque claramente no se irá a ningún lado pronto.

9.3 El proceso de la prueba de hipótesis nula

Podemos descomponer el proceso de la prueba de hipótesis nula en un número de pasos:

1. Formula una hipótesis que represente nuestra predicción (antes de ver los datos).
2. Especifica las hipótesis nula y alternativa.
3. Recolecta datos relevantes para la hipótesis.
4. Ajusta el modelo a los datos que representen la hipótesis alternativa y calcula un estadístico de prueba.
5. Calcula la probabilidad del valor observado de ese estadístico asumiendo que la hipótesis nula es verdadera.
6. Evalúa la “significatividad estadística” del resultado.

Para un ejemplo práctico, usemos la base de datos NHANES para hacernos la siguiente pregunta: ¿La actividad física está relacionada con el índice de masa corporal? En NHANES, los participantes respondieron si se involucran regularmente en deportes moderados o de intensidad vigorosa, fitness, o actividades recreativas (guardado en la variable \(PhysActive\)). Lxs investigadorxs también midieron la altura y el peso y los usaron para calcular el Índice de Masa Corporal (IMC, o BMI por el término en inglés Body Mass Index):

\[ IMC = \frac{peso(kg)}{altura(m)^2} \]

9.3.1 Paso 1: Formular una hipótesis de interés

Hipotetizamos que el IMC es mayor en las personas que no se involucran en actividades físicas, comparado con aquellas que sí lo hacen.

9.3.2 Paso 2: Especifica las hipótesis nula y alternativa

Para el paso 2, necesitamos especificar nuestra hipótesis nula (que llamaremos \(H_0\)) y nuestra hipótesis alternativa (que llamaremos \(H_A\)). \(H_0\) es la línea base contra la que probamos nuestra hipótesis de interés: esto es, ¿cómo esperaríamos que se vieran los datos si no hubiera un efecto? La hipótesis nula siempre involucra algún tipo de igualdad (=, \(\le\), o \(\ge\)). \(H_A\) describe lo que esperaríamos si realmente hubiera un efecto. La hipótesis alternativa siempre involucra algún tipo de diferencia/desigualdad (\(\ne\), >, o <). De manera importante, la prueba de hipótesis nula opera bajo la suposición de que la hipótesis nula es verdadera a menos que la evidencia demuestre lo contrario.

También tenemos que decidir si queremos probar una hipótesis direccional o no direccional. Una hipótesis no direccional simplemente predice que habrá una diferencia, sin predecir en qué dirección irá. Para el ejemplo de IMC/actividad, una hipótesis nula no direccional sería:

\(H0: IMC_{activo} = IMC_{inactivo}\)

y la correspondiente hipótesis alternativa no direccional sería:

\(HA: IMC_{activo} \neq IMC_{inactivo}\)

Una hipótesis direccional, por otro lado, predice en qué dirección irá la diferencia. Por ejemplo, tenemos conocimiento previo fuerte para predecir que la gente que se involucre en actividad física debería pesar menos que aquellos que no lo hacen, por lo tanto podríamos proponer la siguiente hipótesis nula direccional:

\(H0: IMC_{activo} \ge IMC_{inactivo}\)

y la alternativa direccional:

\(HA: IMC_{activo} < IMC_{inactivo}\)

Como veremos más tarde, probar una hipótesis no direccional es más conservador, por lo que esto es lo que generalmente se prefiere a menos que haya alguna razón fuerte a priori para hipotetizar un efecto en una dirección en particular. ¡Las hipótesis, incluyendo si son direccionales o no, siempre deberán ser especificadas antes de ver los datos!

9.3.3 Paso 3: Recolectar datos

En este caso, seleccionaremos una muestra de 250 personas de la base de datos NHANES. La Figura 9.1 muestra un ejemplo de esa muestra, con el IMC mostrado separando a las personas activas e inactivas, y la Tabla 9.1 muestra un resumen estadístico de cada grupo.

Tabla 9.1: Resumen de datos de IMC para personas activas vs inactivas

PhysActive	N	mean	sd
No	131	30	9.0
Yes	119	27	5.2

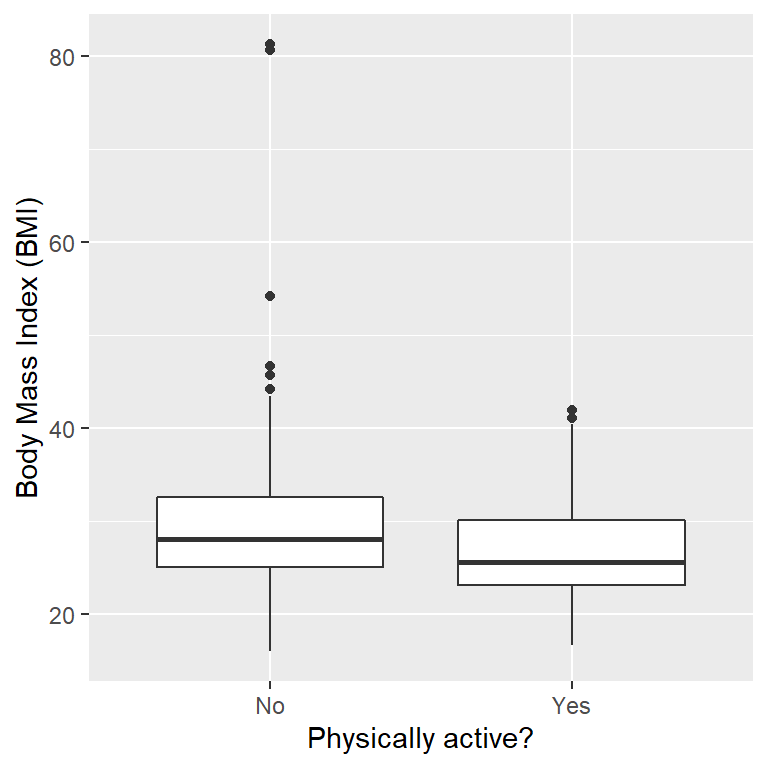
Figura 9.1: Gráfica de cajas (boxplot) de los datos de IMC de una muestra de personas adultas de NHANES, divididas según reportaron involucrarse en actividad física regular.

9.3.4 Paso 4: Ajusta un modelo a los datos y calcula el estadístico de prueba

Después queremos usar los datos para calcular un estadístico que ultimadamente nos permitirá decidir si la hipótesis nula es rechazada o no. Para hacer esto, el modelo necesita cuantificar la cantidad de evidencia en favor de la hipótesis alternativa, relativa a la variabilidad en los datos. Por lo que podemos pensar en el estadístico de prueba como el que provee una medida del tamaño del efecto comparado con la variabilidad en los datos. En general, este estadístico de prueba tendrá una distribución de probabilidad asociada con él, porque eso nos permitirá determinar qué tan probable es nuestro valor estadístico observado bajo la hipótesis nula.

Para el ejemplo de IMC, necesitamos un estadístico de prueba que nos permita probar si hay una diferencia entre dos medias, puesto que las hipótesis están elaboradas en términos de la media de IMC en cada grupo. Un estadístico que es frecuentemente usado para comparar dos medias es el estadístico t, desarrollado primero por el estadístico William Sealy Gossett, quien trabajó para la Guiness Brewery en Dublín y escribió bajo el pseudónimo “Student” - por eso, es frecuentemente llamada “estadístico t de Student.” El estadístico t es apropiado para comparar las medias de dos grupos cuando los tamaños de muestra son relativamente pequeños y la desviación estándar de la población es desconocida. El estadístico t para comparar dos grupos independientes es calculado de la siguiente manera:

\[ t = \frac{\bar{X_1} - \bar{X_2}}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}} \]

donde \(\bar{X}_1\) y \(\bar{X}_2\) son las medias de los dos grupos, \(S^2_1\) y \(S^2_2\) son las varianzas estimadas de los grupos, y \(n_1\) y \(n_2\) son los tamaños de cada grupo. Debido a que la varianza de las diferencias entre dos variables independientes es igual a la suma de las varianzas de cada variable separada (\(var(A - B) = var(A) + var(B)\)), entonces sumamos las varianzas de cada grupo divididas entre sus tamaños de muestras para poder calcular el error estándar de la diferencia (standard error of the difference). Por lo tanto, uno puede ver al estadístico t como una manera de cuantificar qué tan grande es la diferencia entre los grupos en relación con la variabilidad muestral de la diferencia entre las medias.

El estadístico t se distribuye de acuerdo a una distribución de probabilidad conocida como distribución t. La distribución t se mira muy similar a una distribución normal, pero difiere dependiendo del número de grados de libertad (degrees of freedom). Cuando la cantidad de grados de libertad es grande (digamos 1,000), entonces la distribución t se mira esencialmente como una distribución normal, pero cuando es pequeña entonces la distribución t tiene colas más largas que la normal (ve la Figura 9.2). En el caso más simple, donde los grupos son del mismo tamaño y tienen varianzas iguales, los grados de libertad para la prueba t son el número de observaciones menos 2, porque hemos calculado dos medias y por lo tanto hemos renunciado a dos grados de libertad. En este caso es bastante obvio a partir de ver el diagrama de cajas (box plot) que el grupo inactivo es más variable que el grupo activo, y los tamaños de muestra son diferentes en cada grupo, por lo que necesitamos usar una fórmula un poco más compleja para calcular los grados de libertad, a la cual se le conoce comúnmente como prueba t de Welch (Welch t-test). La fórmula es:

\[ \mathrm{d.f.} = \frac{\left(\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}\right)^2}{\frac{\left(S_1^2/n_1\right)^2}{n_1-1} + \frac{\left(S_2^2/n_2\right)^2}{n_2-1}} \] Esta fórmula nos dará un resultado igual a \(n_1 + n_2 - 2\) cuando las varianzas y los tamaños de muestras sean iguales; de otra manera será un resultado menor, aplicando una penalización sobre la prueba debido a las diferencias en los tamaños de muestra o varianzas. Para este ejemplo, el resultado es 241.12 grados de libertad, que es ligeramente menor que el valor de 248 que obtendríamos si restamos 2 a la suma de los tamaños de muestra.

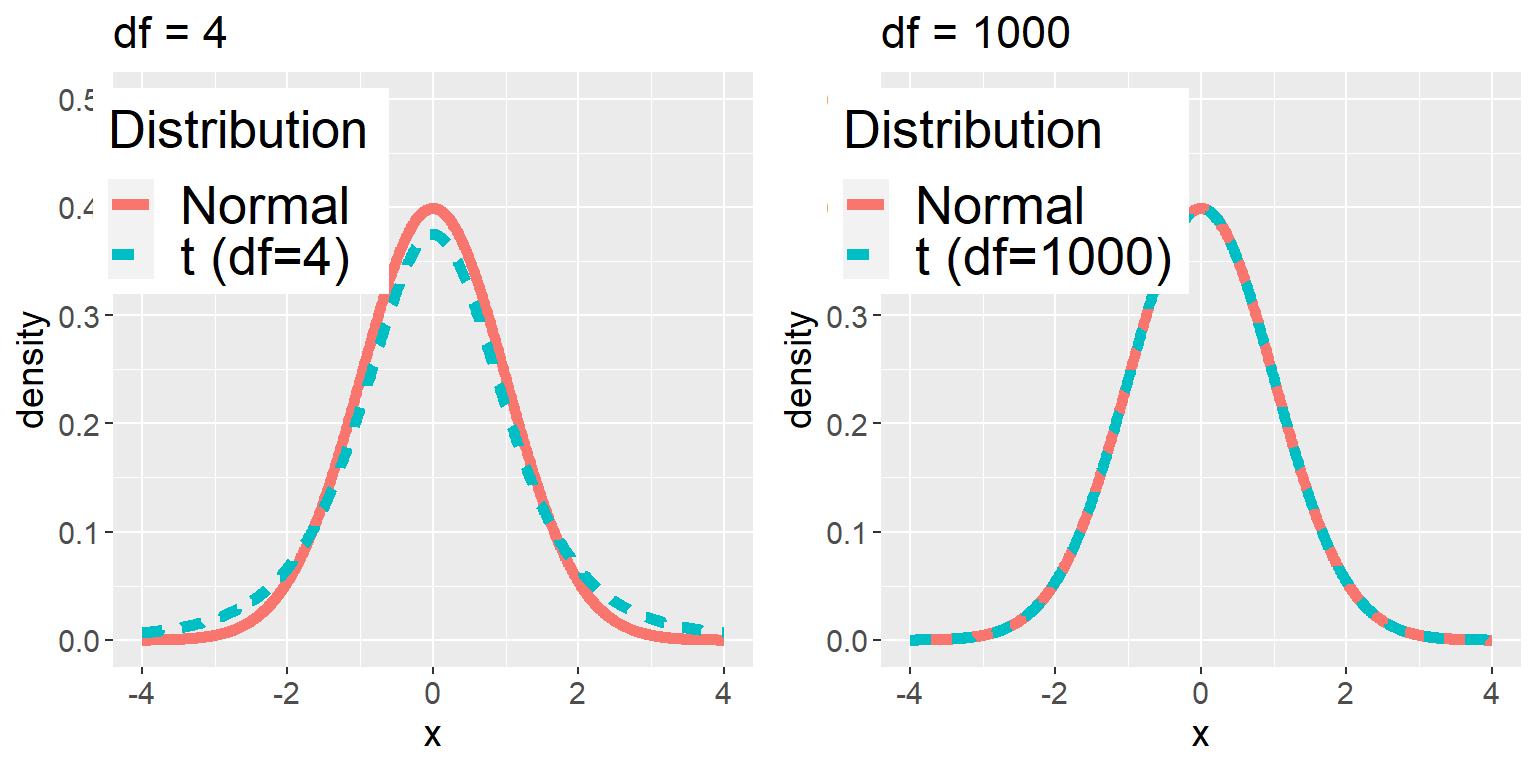
Figura 9.2: Cada panel muestra la distribución t (la línea azul punteada) sobrepuesta a la distribución normal (la línea roja continua). El panel izquierdo muestra una distribución t con 4 grados de libertad, en cuyo caso la distribución es similar pero tiene colas ligeramente más anchas. El panel derecho muestra una distribución t con 1000 grados de libertad, en cuyo caso es virtualmente idéntica a la normal.

9.3.5 Paso 5: Determinar la probabilidad de los resultados observados bajo la hipótesis nula

Este es el paso donde la NHST comienza a ir contra nuestra intuición. En lugar de determinar la probabilidad de que la hipótesis nula sea cierta dados los datos obtenidos, en su lugar determinamos la probabilidad (likelihood) bajo la hipótesis nula de observar un estadístico al menos tan extremo como el que hemos observado — ¡porque comenzamos los pasos asumiendo que la hipótesis nula es verdadera! Para hacer esto, necesitamos conocer la distribución de probabilidad esperada del estadístico bajo la hipótesis nula, de tal manera que podamos preguntar qué tan probable (likely) sería el resultado bajo esa distribución. Nota que cuando digo “qué tan probable (likely) sería el resultado,” lo que realmente quiero decir es “qué tan probable (likely) sería el resultado observado o uno más extremo.” Existen (por lo menos) dos razones por las que necesitamos agregar esta advertencia. La primera es porque cuando hablamos de valores continuos, la probabilidad de cualquier valor particular es cero (lo que recordarás si has tomado un curso de cálculo). De manera más importante, la segunda razón es porque estamos tratando de determinar qué tan raro sería nuestro resultado si la hipótesis nula fuera verdadera, por lo que cualquier resultado que sea más extremo sería incluso más raro, por lo que querremos contar todas esas posibilidades más raras cuando calculemos la probabilidad de nuestro resultado bajo la hipótesis nula.

Podemos obtener esta “distribución nula” ya sea usando una distribución teórica (como la distribución t), o usando aleatorización. Antes de movernos al ejemplo de IMC, comencemos con unos ejemplos más sencillos.

9.3.5.1 Valores p: Un ejemplo muy sencillo

Digamos que queremos determinar si una moneda en particular está sesgada a caer cara. Para recolectar datos, lanzamos la moneda 100 veces, y digamos que contamos 70 caras. En este ejemplo, \(H_0: P(cara) \le 0.5\) y \(H_A: P(cara) > 0.5\), y nuestro estadístico de prueba es simplemente el número de caras que contamos. La pregunta que entonces queremos hacernos es: ¿Qué tan probable es que hubiéramos observado 70 o más caras en 100 lanzamientos de moneda si la probabilidad verdadera de obtener cara es 0.5? Podríamos imaginar que esto podría suceder muy ocasionalmente sólo por azar, pero no parece muy probable. Para cuantificar esta probabilidad, podemos usar la distribución binomial:

\[ P(X \le k) = \sum_{i=0}^k \binom{N}{k} p^i (1-p)^{(n-i)} \] Esta ecuación nos dirá la probabilidad de tener un cierto número de caras (\(k\)) o menos, dada una probabilidad en particular de obtener cara (\(p\)) y un número de eventos (\(N\)). Sin embargo, lo que realmente queremos saber es la probabilidad de un cierto número o más, que podemos obtener restando el resultado de uno, basados en las reglas de probabilidad:

\[ P(X \ge k) = 1 - P(X < k) \]

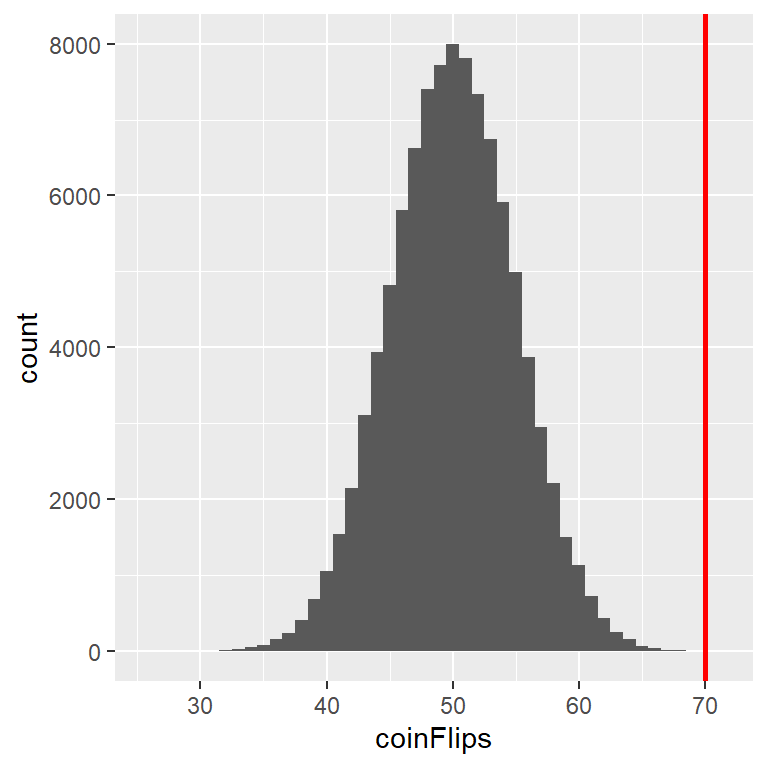
Figura 9.3: Distribución de cantidad de caras (de un total de 100 lanzamientos) a lo largo de 100,000 simulaciones con el valor de 70 representado por la línea vertical.

Usando la distribución binomial, la probabilidad de 69 o menos caras dado P(cara)=0.5 es 0.999961, por lo tanto la probabilidad de 70 o más caras es simplemente uno menos ese valor (0.000039). Este cálculo nos muestra que la probabilidad de obtener 70 o más caras si la moneda efectivamente estuviera balanceada (no trucada) es muy pequeña.

Ahora, ¿qué pasaría si no tuviéramos una función estándar que nos dijera la probabilidad de ese número de caras? Entonces podríamos determinarla por medio de una simulación – repetidamente lanzar la moneda 100 veces usando una probabilidad verdadera de 0.5, y luego calcular la distribución del número de caras a lo largo de estas simulaciones. La Figura 9.3 muestra el resultado de esta simulación. Aquí podemos ver que la probabilidad calculada a través de simulación (0.000030) es muy cercana a la probabilidad teórica (0.000039).

9.3.5.2 Calcular valores p usando la distribución t

Ahora calculemos el valor p para nuestro ejemplo de IMC/actividad usando la distribución t. Primero, calculamos el estadístico t usando los valores de nuestra muestra que calculamos arriba, donde encontramos que t = 3.86. La pregunta que entonces queremos hacernos es: ¿Cuál es la probabilidad de que encontráramos un estadístico t de este tamaño, si la diferencia verdadera entre grupos fuera cero o menor (i.e. la dirección de la hipótesis nula)?

Podemos usar la distribución t para determinar esta probabilidad. Arriba aclaramos que los grados de libertad apropiados (después de corregirlos debido a las diferencias en las varianzas y tamaños de muestras) eran t = 241.12. Podemos usar una función de nuestro software estadístico para determinar la probabilidad de encontrar un valor del estadístico t mayor o igual al observado en nuestra muestra. Encontramos que p(t > 3.86, df = 241.12) = 0.000072, que nos dice que el valor estadístico t observado de 3.86 es relativamente improbable si la hipótesis nula realmente fuera cierta.

En este caso, usamos una hipótesis direccional, por eso sólo tuvimos que observar un lado de la distribución nula. Si hubiéramos querido probar una hipótesis no direccional, entonces tendríamos que haber identificado qué tan inesperado es el tamaño del efecto, sin importar la dirección. En el contexto de la prueba t, eso significa que debemos saber qué tan probable es que el estadístico fuera tan extremo tanto en la dirección positiva como en la negativa. Para hacer esto, multiplicamos el valor t observado por -1, porque la distribución t está centrada alrededor de cero, y luego sumamos juntas las probabilidades de ambas colas para obtener un valor p de dos colas (two-tailed): p(t > 3.86 or t< -3.86, df = 241.12) = 0.000145. Aquí vemos que el valor p para la prueba de dos colas es el doble que para la prueba de una cola, esto refleja el hecho de que un valor extremo es menos sorpresivo porque podría haber ocurrido en cualquier dirección.

¿Cómo eliges si usar una prueba de una cola o de dos colas? La prueba de dos colas siempre será más conservadora, por lo que es una buena apuesta usar esa, a menos que ya tuvieras de antemano una razón fuerte previa para usar una prueba de una cola. En ese caso, tendrías que haber escrito la hipótesis antes de haber visto los datos. En el Capítulo 17 discutiremos la idea del pre-registro de hipótesis, que formaliza la idea de escribir tus hipótesis antes de siquiera haber visto los datos reales. Nunca deberías tomar una decisión de cómo elaborar la hipótesis después de haber visto los datos, porque esto puede introducir sesgos serios en tus resultados.

9.3.5.3 Calcular valores p usando aleatorización

Hasta ahora, hemos visto cómo podemos usar la distribución t para calcular la probabilidad de los datos bajo la hipótesis nula, pero también podemos hacer esto usando simulaciones. La idea básica es que generemos datos simulados similares a los que esperaríamos bajo la hipótesis nula, y luego preguntarnos qué tan extremo es el dato observado en comparación con esos datos simulados. La pregunta clave es: ¿Cómo podemos generar datos para los cuales la hipótesis nula es verdadera? La respuesta general es que podemos reordenar nuestros datos de manera aleatoria en una manera particular que haga que los datos se vean como se deberían ver si la nula fuera realmente verdadera. Esto es similar a la idea de bootstrapping, en el sentido de que usa nuestros propios datos para obtener una respuesta, pero lo hace de una manera diferente.

9.3.5.4 Aleatorización: un ejemplo simple

Comencemos con un ejemplo simple. Digamos que queremos comparar la habilidad promedio de hacer sentadillas de jugadores de football (FB) contra corredores de campo (XC, cross-country runners), con \(H_0: \mu_{FB} \le \mu_{XC}\) y \(H_A: \mu_{FB} > \mu_{XC}\). Medimos la habilidad máxima de hacer sentadillas de 5 jugadores de football y de 5 corredores de campo (que generaremos aleatoriamente, asumiendo que \(\mu_{FB} = 300\), \(\mu_{XC} = 140\), and \(\sigma = 30\)). Los datos se muestran en la Tabla 9.2.

Tabla 9.2: Squatting data for the two groups

group	squat	shuffledSquat
FB	265	125
FB	310	230
FB	335	125
FB	230	315
FB	315	115
XC	155	335
XC	125	155
XC	125	125
XC	125	265
XC	115	310

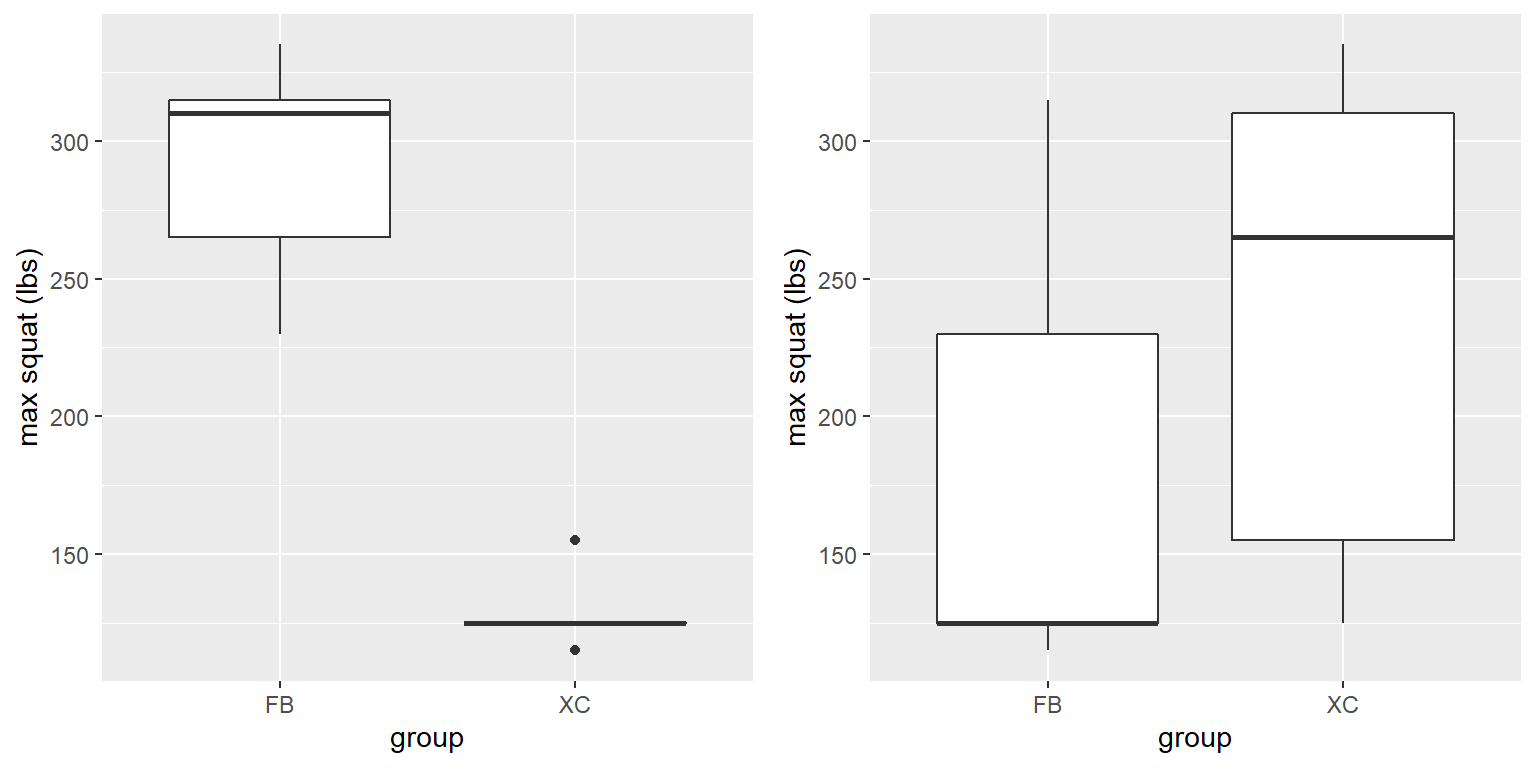
Figura 9.4: Izquierda: Boxplot de la simulación de habilidad de hacer sentadillas de jugadores de football y de corredores de campo. Derecha: Boxplots para sujetos asignados a cada grupo después de revolver las etiquetas de grupo.

En la sección izquierda de la Figura 9.4 es claro que hay una gran diferencia entre los dos grupos. Podemos aplicar una prueba t estándar para probar nuestra hipótesis; para este ejemplo usaremos el comando t.test() en R, que nos da el siguiente resultado:

## 
##  Welch Two Sample t-test
## 
## data:  squat by group
## t = 8, df = 5, p-value = 2e-04
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  121 Inf
## sample estimates:
## mean in group FB mean in group XC 
##              291              129

Si miramos el valor p reportado aquí, vemos que la probabilidad de tal diferencia bajo la hipótesis nula es muy pequeña, usando la distribución t para definir la nula.

Ahora veamos cómo podemos responder la misma pregunta usando aleatorización. La idea básica es que si la hipótesis nula de no diferencia entre grupos es verdadera, entonces no debería importar de qué grupo proviene cada participante (jugadores de football versus corredores de campo) – por eso, para crear datos que son como nuestros datos observados pero que se conforman a la hipótesis nula, podemos reordenar aleatoriamente los datos para cada persona, y luego recalcular la diferencia entre los grupos. Los resultados de tal barajado se muestran en la columna etiquetada “shuffleSquat” en la Tabla 9.2, y los boxplots de los datos resultantes están en el panel derecho de la Figura 9.4.

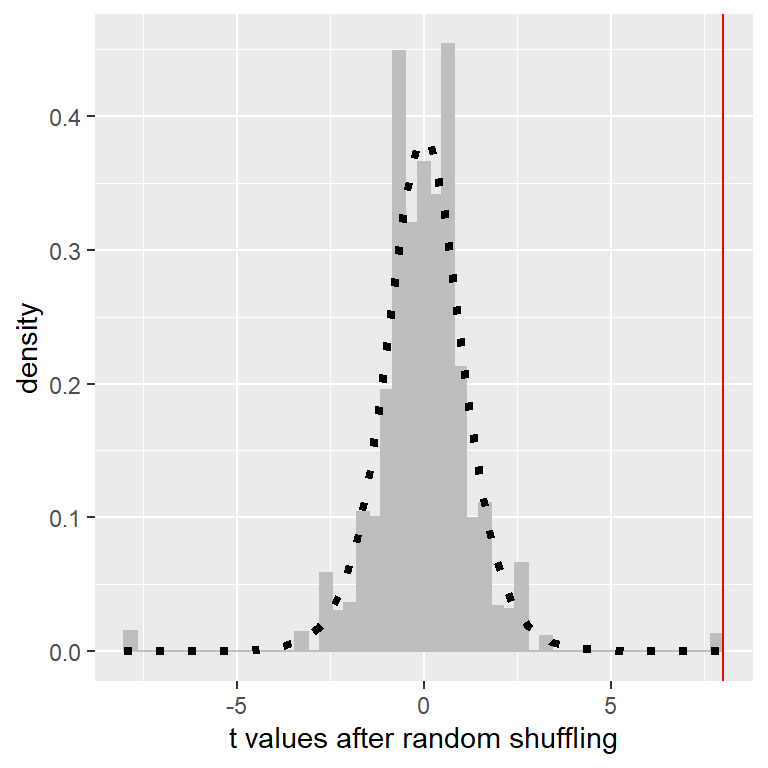
Figura 9.5: Histograma de valores t para la diferencia de medias entre los grupos de jugadores de football y corredores de campo después de barajar la pertenencia al grupo. La línea vertical denota la diferencia real entre los dos grupos, y la línea punteada muestra la distribución t teórica para este análisis.

Después de revolver las etiquetas, vemos que los dos grupos son ahora mucho más similares, y de hecho el grupo de corredores de campo ahora tiene una media ligeramente mayor. Ahora hagamos eso 10,000 veces y guardemos el estadístico t para cada iteración; si estás haciendo esto en tu computadora, tomará un momento en completarse. La Figura 9.5 muestra el histograma de los valores t a lo largo de todas las barajadas aleatorias. Como se esperaba bajo la hipótesis nula, la distribución está centrada en cero (la media de la distribución es 0.007). De la figura podemos ver también que la distribución de los valores t después de barajar sigue aproximadamente la distribución t teórica bajo la hipótesis nula (con media = 0), mostrando que la aleatorización funcionó para generar datos nulos. Podemos calcular el valor p a partir de estos datos aleatorizados al medir cuántos de estos valores barajados son tan o más extremos que el valor observado: p(t > 8.01, df = 8) usando aleatorización = 0.00410. Este valor p es muy similar al valor p que obtuvimos usando la distribución t, y ambos son bastante extremos, sugiriendo que los datos observados son muy improbables que hubieran surgido si la hipótesis nula fuera cierta - y en este caso nosotros sabemos que no es cierta, porque nosotros generamos los datos.

9.3.5.4.1 Aleatorización: ejemplo IMC/actividad

Ahora usemos la aleatorización para calcular el valor p del ejemplo de IMC/actividad. En este caso, vamos a barajar aleatoriamente la variable PhysActive y a calcular la diferencia entre grupos después de cada barajada, y luego comparar nuestro estadístico t observado con la distribución de estadísticos t obtenido de los datos barajados. La Figura 9.6 muestra la distribución de valores t de las muestras barajadas, y podemos calcular la probabilidad de encontrar un valor tan grande o más grande que el valor observado. El valor p obtenido de la aleatorización (0.000000) es muy similar al obtenido usando la distribución t (0.000075). La ventaja de la prueba de aleatorización es que no requiere que asumamos que los datos de cada grupo tienen una distribución normal, aunque la prueba t es generalmente bastante robusta a violaciones de esta suposición. Además de eso, la prueba de aleatorización nos puede permitir calcular valores p para estadísticos cuando no tenemos una distribución teórica como la que tenemos para la prueba t.

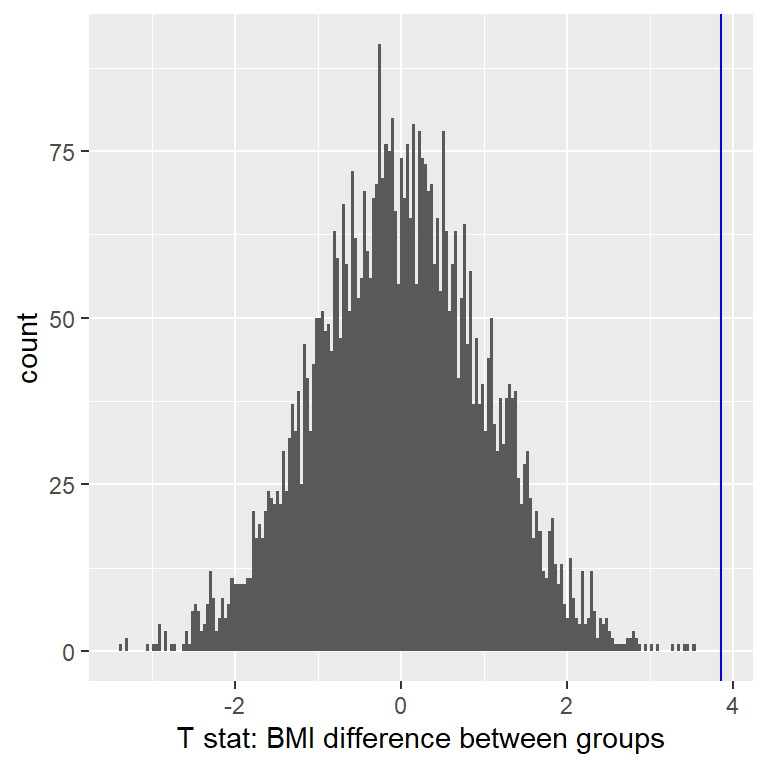
Figura 9.6: Histograma de estadísticos t después de barajar las etiquetas de grupos, con el valor observado del estadístico t mostrado en la línea vertical, y los valores tan extremos o más extremos que el valor observado mostrados en gris más claro.

Sí tenemos que hacer una suposición principal cuando usamos la prueba de aleatorización, a la que nos referimos como intercambiabilidad (exchangeability). Esto significa que todas las observaciones están distribuidas de la misma manera, de tal manera que podemos intercambiarlas sin cambiar la distribución en general. El principal lugar donde esto no se cumple es cuando tenemos observaciones relacionadas en los datos; por ejemplo, si tuviéramos datos de personas en 4 diferentes familias, entonces no podríamos asumir que los individuos son intercambiables, porque los hermanos serían más parecidos unos a otros de lo que serían a individuos de otras familias. En general, si los datos se obtuvieron de un muestreo aleatorio, entonces la suposición de intercambiabilidad se debería sostener.

9.3.6 Paso 6: Evalúa la “significatividad estadística” del resultado

El siguiente paso es determinar si el valor p que resultó del paso previo es suficientemente pequeño para que estemos dispuestos a rechazar la hipótesis nula y concluir en su lugar que la alternativa es correcta. ¿Qué tanta evidencia necesitamos? Esta es una de las preguntas más controversiales en estadística, en parte porque requiere un juicio subjetivo – no hay una respuesta “correcta.”

Históricamente, la respuesta más común a esta pregunta ha sido que deberíamos rechazar la hipótesis nula si el valor p es menor a 0.05. Esto viene de los escritos de Ronald Fisher, quien ha sido referenciado como “la figura individual más importante en la estadística del siglo 20” (Efron 1998):

“Si P está entre .1 y .9 ciertamente no hay razón para sospechar de la hipótesis probada. Si es menor a .02 indica fuertemente que la hipótesis falla en dar cuenta de todos los hechos. No fallaremos frecuentemente si dibujamos una línea convencional en .05 … es conveniente dibujar la línea en el nivel en el que podamos decir: O hay algo en el tratamiento, o una coincidencia ha sucedido de tal manera que no sucede más de una vez cada veinte ensayos” (R. A. Fisher 1925)

Sin embargo, Fisher nunca tuvo la intención de que \(p < 0.05\) fuera una regla fija:

“ningún trabajor científico tiene un nivel fijo de significatividad con el cual, año con año, y en todas las circunstancias, él rechace hipótesis; en su lugar él considera cada caso en particular a la luz de la evidencia y de sus ideas” (Ronald Aylmer Fisher 1956)

En cambio, es probable que p < .05 se convirtió en un ritual debido a la dependencia en tablas de valores p que fueron usadas antes de que las computadoras hicieran fácil el calcular valores p para valores arbitrarios de un estadístico. Todas las tablas tenían una entrada para 0.05, haciendo fácil determinar si el estadístico en nuestros datos excedía el valor requerido para alcanzar ese nivel de significatividad.

La elección de umbrales estadísticos se mantiene profundamente controversial, y recientemente (Benjamin et al., 2018) se ha propuesto que el umbral por defecto sea cambiado de .05 a .005, haciendo sustancialmente más estricto y por lo tanto más difícil el rechazar la hipótesis nula. En gran medida este movimiento ha surgido por preocupaciones crecientes de que la evidencia obtenida de un resultado significativo al nivel \(p < .05\) sea relativamente débil; regresaremos a esto en nuestra futura discusión sobre reproducibilidad en el Capítulo 17.

9.3.6.1 Prueba de hipótesis como toma de decisiones: la aproximación Neyman-Pearson

Mientras Fisher pensaba que el valor p podría proveer de evidencia sobre una hipótesis específica, los estadísticos Jerzy Neyman y Egon Pearson estaban en desacuerdo de manera vehemente. En su lugar, ellos propusieron que pensáramos en la prueba de hipótesis en términos de su tasa de error en el largo plazo:

“ninguna prueba basada en la teoría de probabilidad puede en sí misma proveer ninguna evidencia de valor sobre la verdad o falsedad de una hipótesis. Pero podríamos darle un vistazo al propósito de las pruebas desde otro punto de vista. Sin esperar conocer si cada hipótesis separada es verdadera o falsa, podríamos buscar reglas que gobiernen nuestro comportamiento respecto a ellas, que siguiéndolas podamos asegurar que, en el largo plazo de la experiencia, no estemos equivocados frecuentemente” (J. Neyman and Pearson 1933)

Esto es: no podemos saber cuáles decisiones específicas son correctas o incorrectas, pero si seguimos las reglas, podemos por lo menos saber qué tan frecuentemente nuestras decisiones serán incorrectas en el largo plazo.

Para entender el marco para toma de decisiones que Neyman y Pearson desarrollaron, primero necesitamos discutir la toma de decisiones estadísticas en términos de los tipos de resultados que pueden ocurrir. Existen dos posibles estados de la realidad (\(H_0\) es verdadera, o \(H_0\) es falsa), y dos posibles decisiones (rechazar \(H_0\), o conservar \(H_0\)). Existen dos maneras en que podemos tomar una decisión correcta:

• Podemos rechazar \(H_0\) cuando es falsa (en el lenguaje de la teoría de detección de señales, llamamos a esto un acierto, en inglés hit)
• Podemos conservar \(H_0\) cuando es verdadera (de manera algo confusa en este contexto, llamamos a esto un rechazo correcto)

Existen también dos tipos de errores que podemos cometer:

• Podemos rechazar \(H_0\) cuando realmente es correcta (llamamos a esto una falsa alarma, o un Error Tipo I)
• Podemos conservar \(H_0\) cuando realmente es falsa (llamamos a esto una omisión, en inglés miss, o un Error Tipo II)

Neyman y Pearson acuñaron estos dos términos para describir la probabilidad de estos dos tipos de errores en el largo plazo:

• P(Type I error) = \(\alpha\)
• P(Type II error) = \(\beta\)

Esto es, si definimos un \(\alpha\) en .05, entonces en el largo plazo deberíamos cometer un Error Tipo I el 5% de las veces. Mientras que es común definir un \(\alpha\) en .05, el valor estándar para un nivel aceptable de \(\beta\) es .2 - esto es, estamos dispuestos a aceptar que un 20% del tiempo fallaremos en detectar un verdadero efecto cuando realmente existe. Regresaremos a esto después cuando discutamos poder estadístico en la Sección 10.3, que es el complemento del Error Tipo II.

9.3.7 ¿Qué significa un resultado significativo?

Existe mucha confusión sobre lo que realmente significan los valores p (Gigerenzer, 2004). Digamos que hacemos un experimento comparando las medias entre condiciones, y encontramos una diferencia con un valor p de .01. Hay varias interpretaciones posibles que podrían plantearse.

9.3.7.1 ¿Significa que la probabilidad de que la hipótesis nula sea verdadera es .01?

No. Recuerda que en la prueba de hipótesis nula, el valor p es la probabilidad de los datos dada la hipótesis nula (\(P(data|H_0)\)). No garantiza conclusiones acerca de la probabilidad de la hipótesis nula dados los datos (\(P(H_0|data)\)). Regresaremos a esta pregunta cuando discutamos la inferencia Bayesiana en un capítulo posterior, porque el teorema de Bayes nos permite invertir la probabilidad condicional de una manera que nos permite determinar la probabilidad de la hipótesis dados los datos.

9.3.7.2 ¿Significa que la probabilidad de que estés tomando la decisión incorrecta es .01?

No. Esto sería \(P(H_0|data)\), pero recuerda, como mencionamos arriba, que los valores p son probabilidades de los datos bajo \(H_0\), no probabilidades de las hipótesis.

9.3.7.3 ¿Significa que si vuelves a hacer el estudio, obtendrías el mismo resultado 99% de las veces?

No. El valor es un enunciado sobre la probabilidad de un conjunto particular de datos bajo la hipótesis nula; no nos permite hacer inferencias sobre la probabilidad de eventos futuros como las replicaciones.

9.3.7.4 ¿Significa que encontraste un efecto importante de manera práctica?

No. Existe una distinción esencial entre significatividad estadística y significatividad práctica. Como ejemplo, digamos que realizamos un ensayo controlado aleatorizado para examinar el efecto de una dieta particular sobre el peso corporal, y encontramos un efecto estadísticamente significativo a nivel p<.05. Lo que esto no nos dice es cuánto peso realmente se bajó, que es a lo que nos referimos como tamaño del efecto (effect size, que será discutido en mayor detalle en el Capítulo 10). Si pensamos en un estudio sobre pérdida de peso, probablemente no pensaremos que el perder una onza (28 gramos, i.e. el peso de una tortilla y media) sea significativo de manera práctica. Démosle un vistazo a nuestra habilidad para detectar una diferencia significativa de 28 gramos conforme el tamaño de la muestra incrementa.

La Figura 9.7 muestra cómo la proporción de resultados significativos incrementa conforme el tamaño de muestra incrementa, con lo cual con una muestra muy grande (cercana a 262,000 sujetos en total), encontraremos un resultado significativo en más del 90% de los estudios donde haya 1 onza de diferencia de peso perdido entre las dietas que estén siendo comparadas. Mientras que estos datos son estadísticamente significativos, la mayoría de los médicos no considerarían la pérdida de peso de una onza como algo significativo de manera práctica o clínica. Exploraremos esta relación en mayor detalle cuando regremos al concepto de poder estadístico en la Sección 10.3, pero debería ser claro en este momento de este ejemplo que la significatividad estadística no es necesariamente indicadora de significatividad práctica.

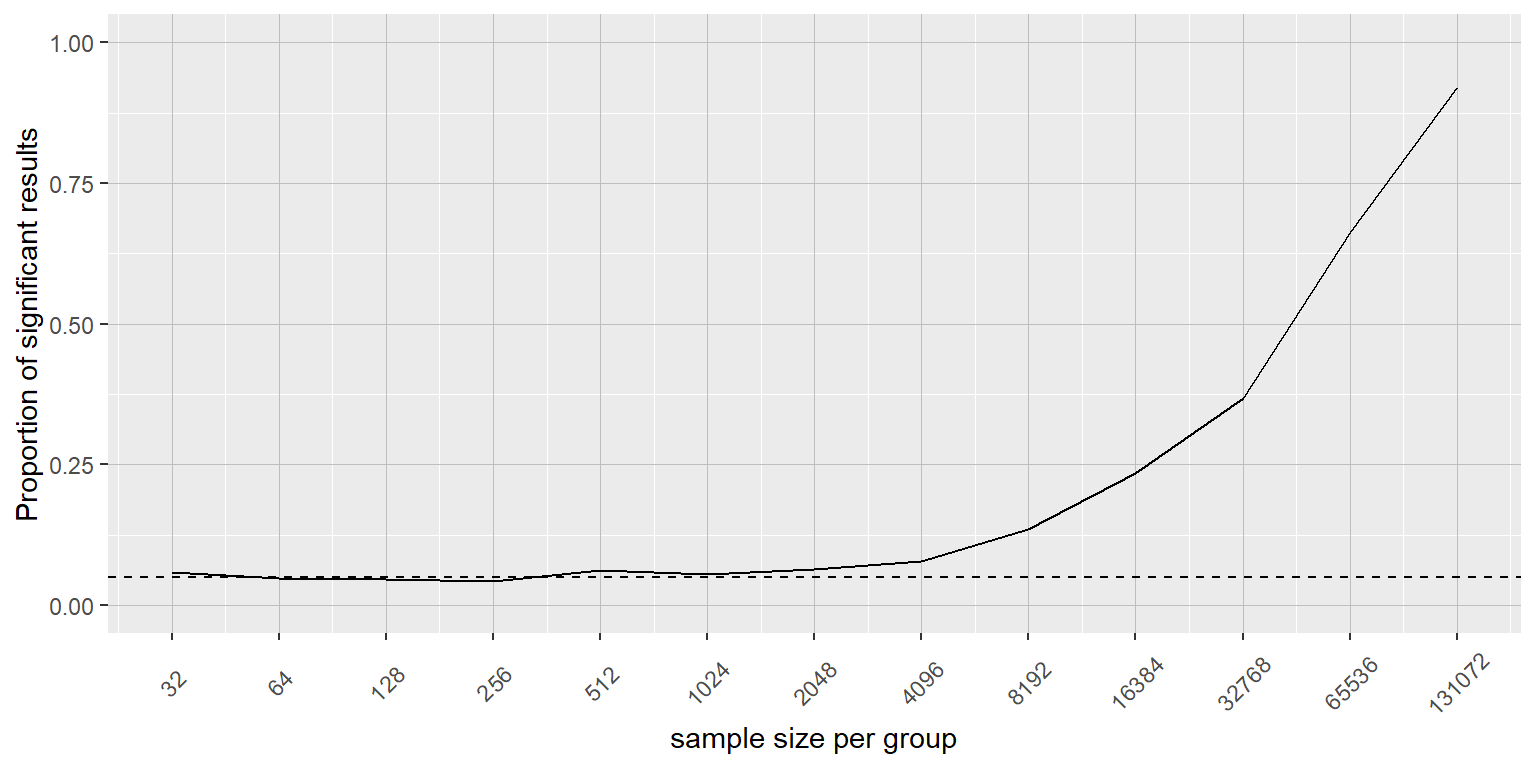
Figura 9.7: La proporción de resultados significativos para un cambio muy pequeño (1 onza = 28 gramos, que es alrededor de .001 desviaciones estándar) como función del tamaño de la muestra.

9.4 NHST en un contexto moderno: Pruebas múltiples

Hasta ahora hemos discutido ejemplos donde estamos interesades en probar una sola hipótesis estadística, y esto es consistente con la ciencia tradicional que frecuentemente sólo medía unas pocas variables a la vez. Sin embargo, en la ciencia moderna frecuentemente medimos millones de variables por persona. Por ejemplo, en estudios genéticos que cuantifican el genoma completo, podría haber varios millones de medidas por persona, y en la investigación en neuroimagen que mi grupo realiza, frecuentemente recolectamos datos de más de 100,000 localizaciones en cada cerebro al mismo tiempo. Cuando la manera estándar de la prueba de hipótesis se aplica en estos contextos, malas cosas pueden suceder a menos que tomemos las medidas apropiadas.

Veamos un ejemplo de cómo podría funcionar esto. Hay un gran interés en entender los factores genéticos que pueden predisponer a las personas a enfermedades mentales como la esquizofrenia, porque sabemos que cerca del 80% de las variaciones entre personas en la presencia de esquizofrenia es debida a diferencias genéticas. El Proyecto de Genoma Humano y la revolución subsecuente en ciencia genómica ha provisto herramientas para examinar las múltiples maneras en que los humanos difieren unos de otros en sus genomas. Una aproximación que ha sido usada en años recientes es conocida como estudios de asociación del genoma completo (genome-wide association study, GWAS), en el cual el genoma para cada persona es caracterizado en un millón o más de lugares para determinar cuáles letras del código genético tienen en cada lugar, concentrándose en lugares donde los humanos tienden a variar frecuentemente. Después de que éstas han sido determinadas, les investigadores realizan una prueba estadística en cada localización del genoma para determinar si las personas diagnosticadas con esquizofrenia tienen mayor o menor probabilidad de tener una versión específica de la secuencia genética en ese lugar del genoma.

Imaginemos qué pasaría si les investigadores simplemente preguntaran si la prueba fue significativa al nivel p<.05 en cada localización, cuando en realidad no hay un efecto verdadero en ninguna de las localizaciones. Para hacer esto, generamos un gran número de valores t simulados de una distribución nula, y preguntamos cuántos de ellos son significativos al nivel p<.05. Hagamos esto muchas veces, y en cada ocasión contemos cuántas de estas pruebas salen significativas (ve la Figura 9.8).

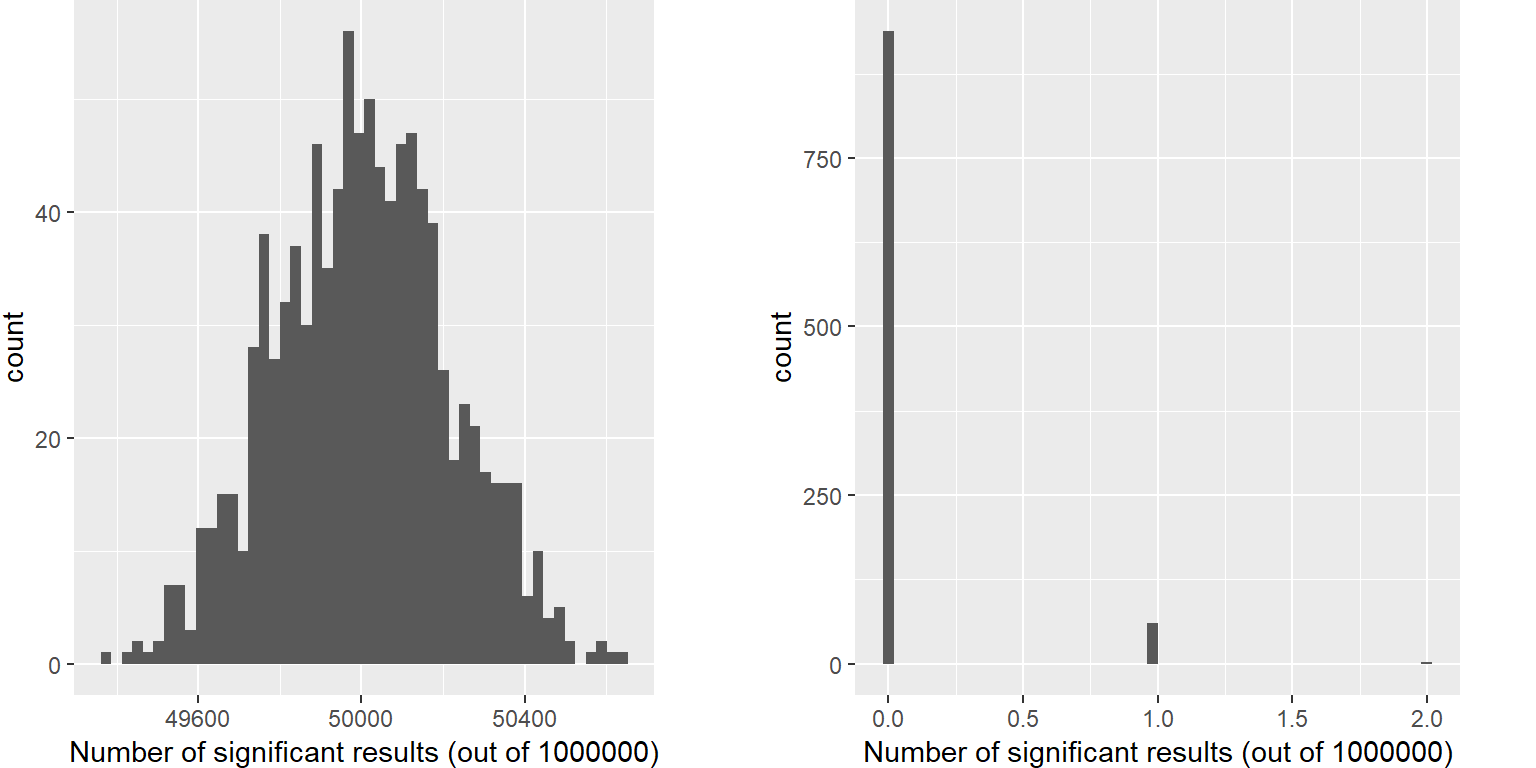
Figura 9.8: Izquierda: Histograma con el número de resultados significativos en cada conjunto de un millón de pruebas estadísticas, cuando en realidad no hay ningún efecto verdadero. Derecha: Histograma con el número de resultados significativos a lo largo de todas las simulaciones después de aplicar la corrección de Bonferroni para pruebas múltiples.

Esto muestra que cerca del 5% de todas las pruebas fueron significativas en cada simulación, significando que si usáramos p < .05 como nuestro umbral para significatividad estadística, entonces a pesar de que no hay ninguna relación presente verdaderamente significativa, aún así “encontraríamos” cerca de 500 genes que parecerían significativos en cada estudio (el número esperado de resultados significativos es simplemente \(n * \alpha\)). Esto es porque mientras controlamos por el error por cada prueba, no controlamos la tasa de errores a lo largo de la familia completa de pruebas (conocido como el error de familia, en inglés familiy-wise error), que es lo que realmente queremos controlar si vamos a observar los resultados de un número grande de pruebas. Usando p<.05, nuestra tasa de error de familia en el ejemplo de arriba es uno – esto es, prácticamente tenemos garantizado el que cometeremos un error en cada estudio en particular.

Una manera simple de controlar este error de familia es dividir el nivel alfa entre el número de pruebas; esto es conocido como la corrección Bonferroni, nombrada en honor al estadístico italiano Carlo Bonferroni. Usando los datos del ejemplo anterior, vemos en la Figura 9.8que sólo cerca del 5 por ciento de los estudios muestra algún resultado significativo usando el nivel de alfa corregido de 0.000005 en lugar del valor nominal de .05. Hemos controlado efectivamente el error de familia, de tal manera que la probabilidad de cometer cualquier error en nuestro estudio está controlado justo alrededor de .05.

9.5 Objetivos de aprendizaje

• Identificar los componentes de una prueba de hipótesis, incluyendo el parámetro de interés, las hipótesis nula y alternativa, y el estadístico de prueba.
• Describir las interpretaciones apropiadas de un valor p así como de las interpretaciones erróneas comunes.
• Distinguir entre los dos tipos de errores en la prueba de hipótesis, y los factores que los determinan.
• Describir cómo el remuestreo puede ser usado para calcular un valor p.
• Describir el problema de múltiples pruebas, y cómo se puede resolver.
• Describir las principales críticas a la prueba estadística de hipótesis nula.

9.6 Lecturas sugeridas

• Mindless Statistics, por Gerd Gigerenzer

Referencias

Efron, Bradley. 1998. “R. A. Fisher in the 21st Century (Invited Paper Presented at the 1996 r. A. Fisher Lecture).” Statist. Sci. 13 (2): 95–122. https://doi.org/10.1214/ss/1028905930.

Fisher, R. A. 1925. Statistical Methods for Research Workers. Edinburgh Oliver & Boyd.

Fisher, Ronald Aylmer. 1956. Statistical Methods and Scientific Inference. New York: Hafner Pub. Co.

Neyman, J., and K. Pearson. 1933. “On the Problem of the Most Efficient Tests of Statistical Hypotheses.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 231 (694-706): 289–337. https://doi.org/10.1098/rsta.1933.0009.