Capitulo 4 Visualización de Datos

El 28 de enero de 1986, el Space Shuttle Challenger explotó 73 segundos después del despegue, matando a lxs 7 astronautas a bordo. Así como cuando los desastres suceden, hubo una investigación oficial sobre lo que ocasionó el accidente. El cual encontró que un “O-ring” (junta tórica) que conectaba dos secciones del sólido populsor de cohete goteó, lo cual resultó en la falla de la unión y explosión del tanque propulsor (véase figura 4.1).

Figura 4.1: Imagen del sólido propulsor de cohete derramando combustible, segundos antes de la explosión. La pequeña flama visible al costado del cohete es el sitio de la falla del O-ring (junta tórica). By NASA (Great Images in NASA Description) [Public domain], via Wikimedia Commons

La investigación encontró que muchos aspectos del proceso de decisión de la NASA tenían errores, y estaban focalizados en una reunión entre el personal de la NASA e ingenierxs de Morton Thiokol, un empresario que construía sólidos propulsores de cohete. Estxs ingenierxs estaban paricularmente preocupadxs por las temperaturas que habían sido pronosticadas para la mañana del lanzamiento, las cuales eran muy bajas. Ellos tenían datos de lanzamientos pasados donde el funcionamiento de los “O-rings” se veían afectados a temperaturas bajas. En la junta previa al lanzamiento, lxs ingenierxs presentaron sus datos a lxs directivxs de la NASA, pero fueron incapaces de convencerles el posponer el lanzamiento. Su evidencia fue una serie de notas escritas a mano mostrando números de los lanzamientos pasados.

El experto en visualización Edward Tufte ha argumentado que con la presentación adecuada de todos los datos, lxs ingenierxs pudieron haber sido mucho más persuasivos. En particular, pudieron haber mostrado una gráfica como la de la Figura 4.2, en la cual subraya dos hechos importantes. Primero, demuestra la cantidad del daño de “O-ring” (definido por la cantidad de erosión y hollín encontrado afuera de los anillos después que el sólido de propulsor de cohete fuera recuperado del océano en vuelos pasados) fue relacionado estrechamente a la temperatura del despegue. Segundo, demuestra que el rango de temperaturas pronosticadas para la mañana del 28 de enero (mostrado en el área sombreada) estaba fuera del rango de todos despegues previos. Aunque no podemos saber con certeza, se ve por lo menos posible que con eso hubieran podido ser más convincentes.

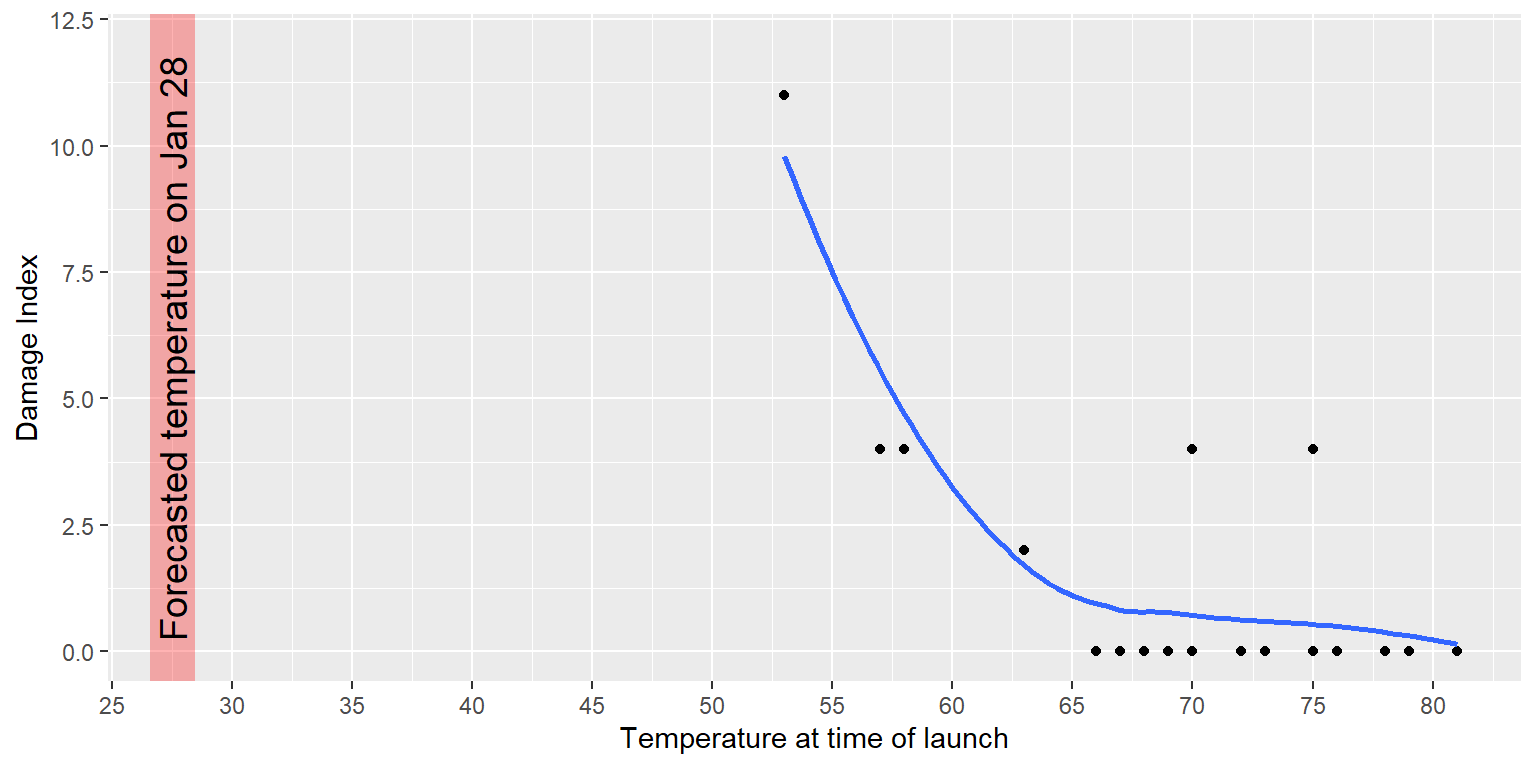
Figura 4.2: Replanteo de los datos del índice de daños de Tufte. La línea muestra la tendencia en los datos y el área sombreada muestra las temperaturas proyectadas para la mañana del lanzamiento.

4.1 Anatomía de una gráfica

El objetivo de graficar datos es presentar un resumen de una base de datos en una presentación bi-dimensional (o en ocasiones, tri-dimensional). Nos referimos a las dimensiones como ejes – el eje horizontal es llamado el eje X y el eje vertical es llamado el eje Y. Podemos acomodar los datos a través de los ejes que enfaticen los valores de los datos. Estos valores pueden ser continuos o categóricos.

Hay muchos tipos de gráficas que se pueden utilizar, las cuales tienen diferentes ventajas y desventajas. Digamos que estamos interesadxs en caracterizar la diferencia de altura en hombres y mujeres en la base de datos NHANES. La figura 4.3 muestra cuatro diferentes maneras de graficar esos datos.

1. La gráfica de barras en el panel A muestra la diferencia en medias (means), pero no nos muestra cuánta dispersión hay en los datos alrededor de estas medias – y como veremos después, saber esto es esencial para determinar si consideramos que la diferencia entre los grupos es suficientemente grande como para ser importante.

2. La segunda gráfica muestra las barras con todos los puntos de datos (data points) sobrepuestos - esto hace un poco más claro que la distribución de la altura de hombres y mujeres se empalman, pero aún es difícil ver debido a la gran cantidad de puntos de datos.

En general preferimos usar una técnica de graficado que provea una vista más clara de la distribución de puntos de datos.

3. En el panel C, podemos ver un ejemplo de gráfica violín, en la cual se grafica la distribución de cada condición de los datos (después de suavizarla un poco).

4. Otra opción es el diagrama de caja (box plot) mostrado en el panel D, en el cual se muestra la mediana (línea central), una medida de variabilidad (lo ancho de la caja, que está basado en una medida llamada rango intercuartílico), y cualquier valor atípico (observado por los puntos al final de las líneas). Ambas son formas efectivas de mostrar datos que proporcionan una buena idea de la distribución de los datos.

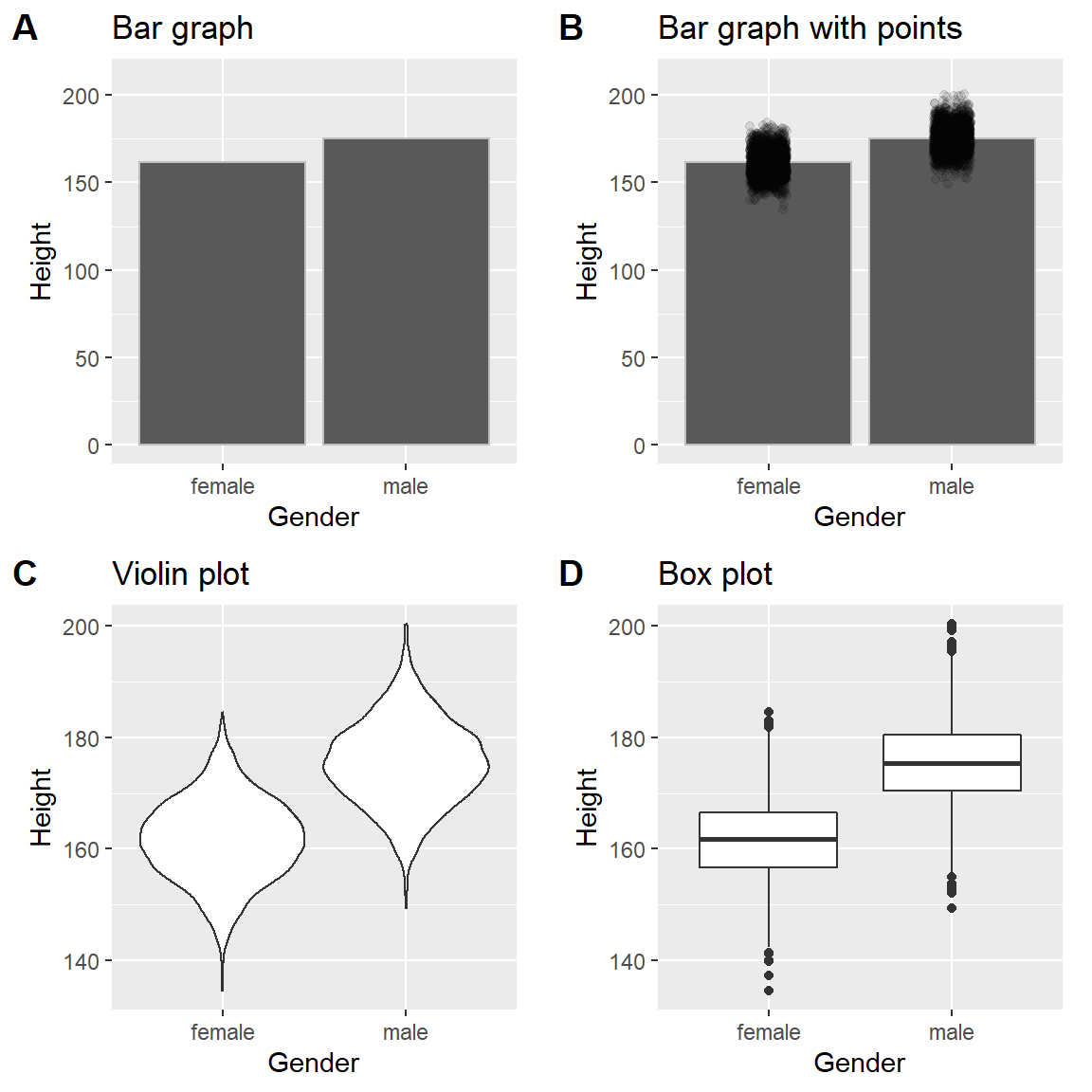
Figura 4.3: Cuatro maneras diferentes de graficar la diferencia en altura entre hombres y mujeres en la base de datos NHANES. El Panel A grafica las medias de ambos grupos, lo que no permite evaluar el empalme relativo entre las dos distribuciones. El Panel B muestra las mismas barras, pero sobrepone los puntos de datos, dispersándolos un poco para que se pueda ver la distribución general. El Panel C muestra una gráfica violín, la cual muestra la distribución de los datos en cada grupo. El Panel D muestra un diagrama de caja (box plot), el cual resalta el ancho de la distribución, además de presentar los valores atípicos (outliers, los cuales se muestran como puntos individuales).

4.2 Principios de una buena visibilización

Se han escrito muchos libros acerca de la visualización efectiva de los datos. Hay algunos principios en los que la mayoría de lxs autorxs están de acuerdo, mientras que otros son más polémicos. Aquí resumimos algunos de los principios fundamentales; si quieres aprender más, algunos buenos recursos están enlistados en la sección de Lecturas sugeridas al final del capítulo.

4.2.1 Muestra los datos y haz que destaquen

Digamos que llevo a cabo un estudio en donde se examine la relación entre salud dental y el tiempo invertido en el uso de hilo dental, y quiero visualizar los datos. La Figura 4.4 muestra cuatro posibles presentaciones de estos datos.

1. En el panel A, en realidad no mostramos los datos, sólo una línea expresando la relación entre los datos. Esto claramente no es óptimo, porque en realidad no podemos ver cómo se ven los datos subyacentes.

Los paneles B-D muestran tres posibles resultados de graficar los datos, en donde cada gráfica muestra una manera diferente en la que los datos se pudieron haber visto.

2. Si vemos la gráfica en el panel B, probablemente desconfiaríamos – raras veces datos reales siguen un patrón tan preciso.
3. Los datos en el panel C, por el otro lado, se ven como datos reales – muestran una tendencia general, pero son desordenados, como suelen ser los datos en el mundo real.
4. Los datos en el panel D nos muestran que la aparente relación entre las dos variables es solamente causada por una persona, a la que nos referiremos como valor atípico (outlier) porque cae muy lejos del patrón del resto del grupo. Debería de ser claro que probablemente no queremos sacar muchas conclusiones de un efecto guiado por un solo punto de los datos. Esta figura resalta por qué es siempre importante mirar los datos sin procesar (o datos crudos, raw data) antes de confiar demasiado en cualquier resumen de los datos.

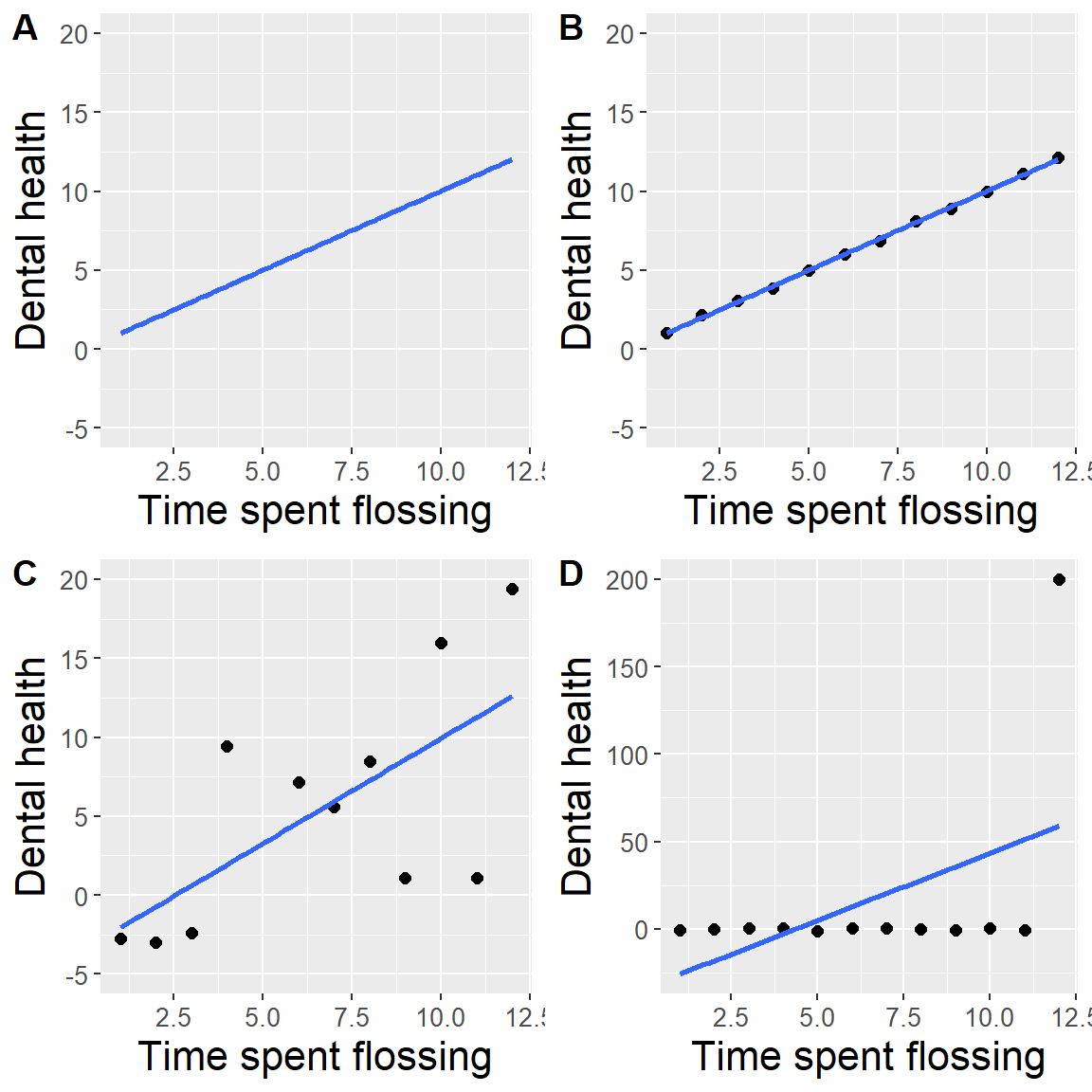
Figura 4.4: Cuatro posibles presentaciones diferentes de datos para el ejemplo de salud dental. Cada punto del gráfico de dispersión representa un punto de datos en el conjunto de datos, y la línea en cada gráfico representa la tendencia lineal en los datos.

4.2.2 Maximiza la proporción datos/tinta (data/ink ratio)

Edward Tufte propuso una idea llamada proporción datos/tinta (data/ink ratio)

\[ data/ink\ ratio = \frac{amount\, of\, ink\, used\, on\, data}{total\, amount\, of\, ink} \]

El punto de esto es minimizar la contaminazión visual y permitir mostrar los datos. Por ejemplo, toma las dos presentaciones sobre la salud dental en la Figura 4.5. Ambos paneles muestran los mismos datos, pero el panel A es mucho más sencillo de comprender, porque es relativamente alta la proporción de datos/tinta.

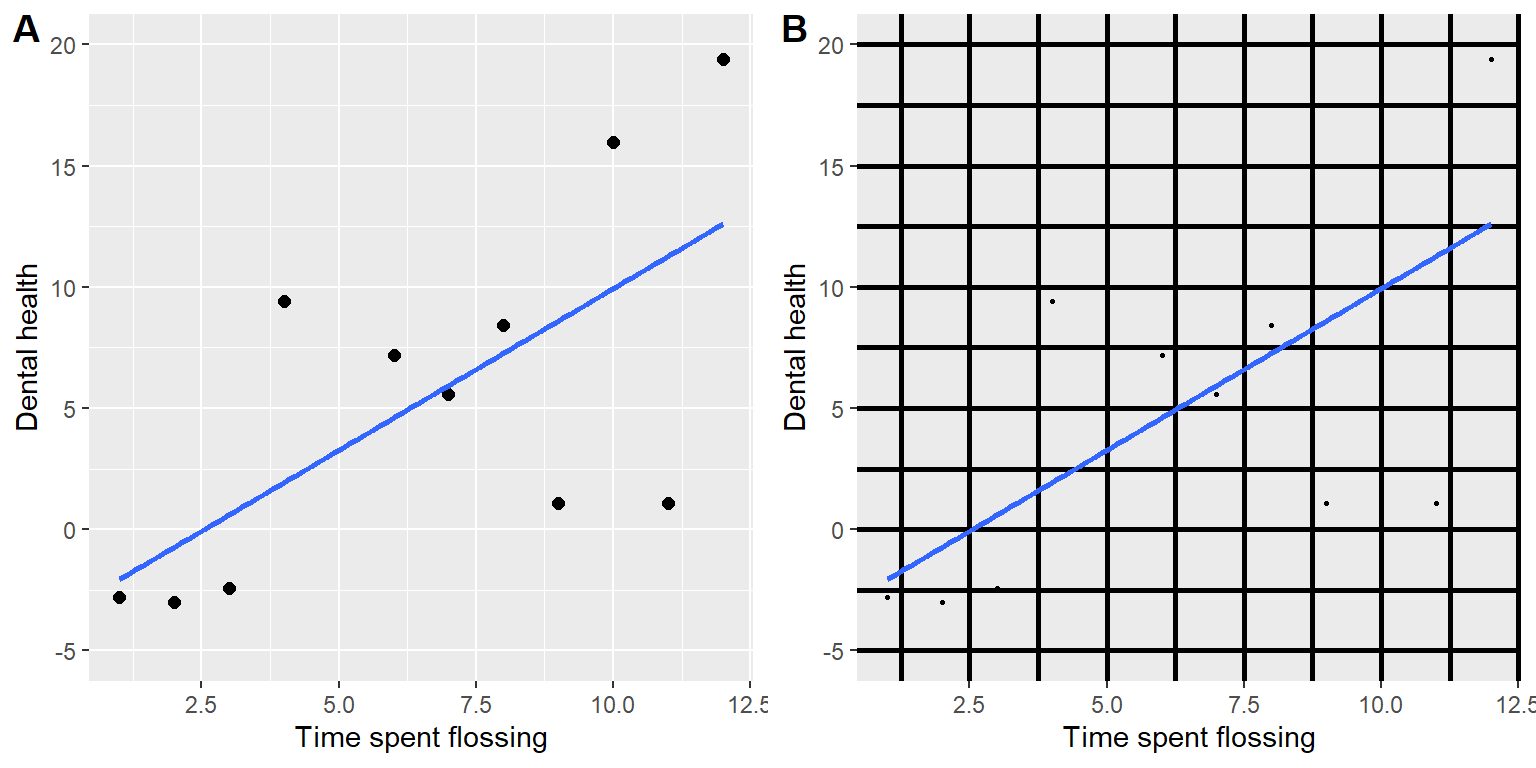
Figura 4.5: Un ejemplo de los mismos datos graficados en dos porporciones datos/tinta diferentes.

4.2.3 Evita gráficas basura

Es especialmente común ver presentaciones de datos en medios populares que son adornados con muchos elementos visuales que son temáticamente relacionados con el contenido pero no relacionados con los datos verdaderos. Esto es conocido como gráficas basura (chartjunk) y debe de ser evitado a toda costa.

Una buena manera de no usar gráficas basura es tratar de evitar programas populares de hojas de cálculo para graficar nuestros datos. Por ejemplo el diagrama en la Figura 4.6 (creado en Microsoft Excel) grafica la popularidad relativa de las diferentes regiones de Estados Unidos. Hay al menos tres cosas mal con esta figura:

• tiene gráficos superpuestos en cada una de las barras que no tienen nada que ver con los datos reales
• tiene una textura de fondo que distrae
• utiliza barras tridimensionales, que distorsionan los datos

Figura 4.6: Un ejemplo de gráfica basura.

4.2.4 Evita distorsionar los datos

En ocasiones es posible usar la visualización para distorsionar el mensaje de un conjunto de datos. Algo muy común es el uso de diferentes escalas de eje para exagerar u ocultar un patrón de datos. Por ejemplo, digamos que estamos interesades en ver si los índices de crímenes violentos han cambiado en Estados Unidos. En la Figura 4.7, podemos ver los datos graficados de manera que en una gráfica parece ser que el crimen ha permanecido constante, pero en la otra parece que se ha desplomado.¡Los mismos datos pueden contar dos historias muy diferentes!

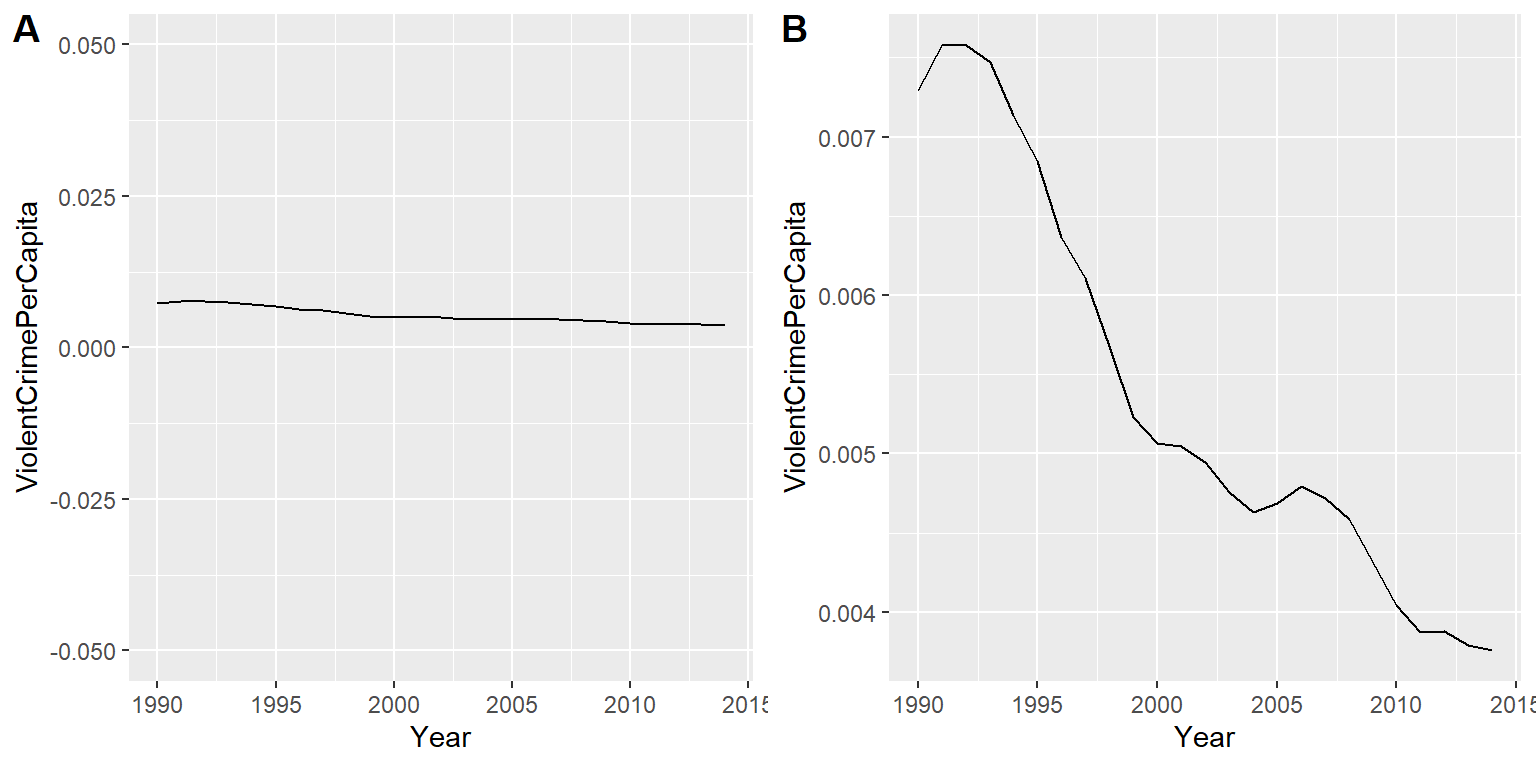
Figura 4.7: Datos de crímenes de 1990 a 2014 graficados con el tiempo. Los paneles A y B muestran los mismos datos pero con diferentes rangos de valores a lo largo del eje Y. Datos obtenidos de https://www.ucrdatatool.gov/Search/Crime/State/RunCrimeStatebyState.cfm

Una de las mayores controversias en la visualización de datos estadísticos es cómo elegir el eje Y, y en particular si se debe de incluir el cero. En su famoso libro “Cómo mentir con estadística,” Darrell Huff argumentó fuertemente que uno siempre debería de incluir el cero en el eje Y. Por otro lado, Edward Tufte ha argumentado en contra de esto:

“En general, en una serie de tiempo, usa una línea de base que muestre los datos y no el punto cero; no gastes mucho espacio vertical vacío tratando de llegar al punto cero a costa de ocultar lo que está sucediendo en la línea de datos en sí” (de: https://qz.com/418083/its-ok-not-to-start-your-y-axis-at-zero/).

Ciertamente, hay ciertos casos en donde usar el punto cero no tiene sentido para nada. Digamos que estamos interesades en graficar la temperatura corporal de un individuo en el tiempo. En la Figura 4.8 graficamos los mismos datos (simulados) con o sin cero en el eje Y. Debería de ser obvio que al graficar estos datos con cero en el eje Y (Panel A) estamos gastando mucho espacio en la figura, ¡dado que la temperatura corporal de una persona viva nunca podría llegar a cero! Al incluir el cero, tambien estamos haciendo el salto de temperatura durante 21-30 días menos evidente. En general, mi inclinación en el caso de gráficas lineales y de dispersión es el usar todo el espacio en la gráfica, a menos que el punto cero sea sumamente importante de resaltar.

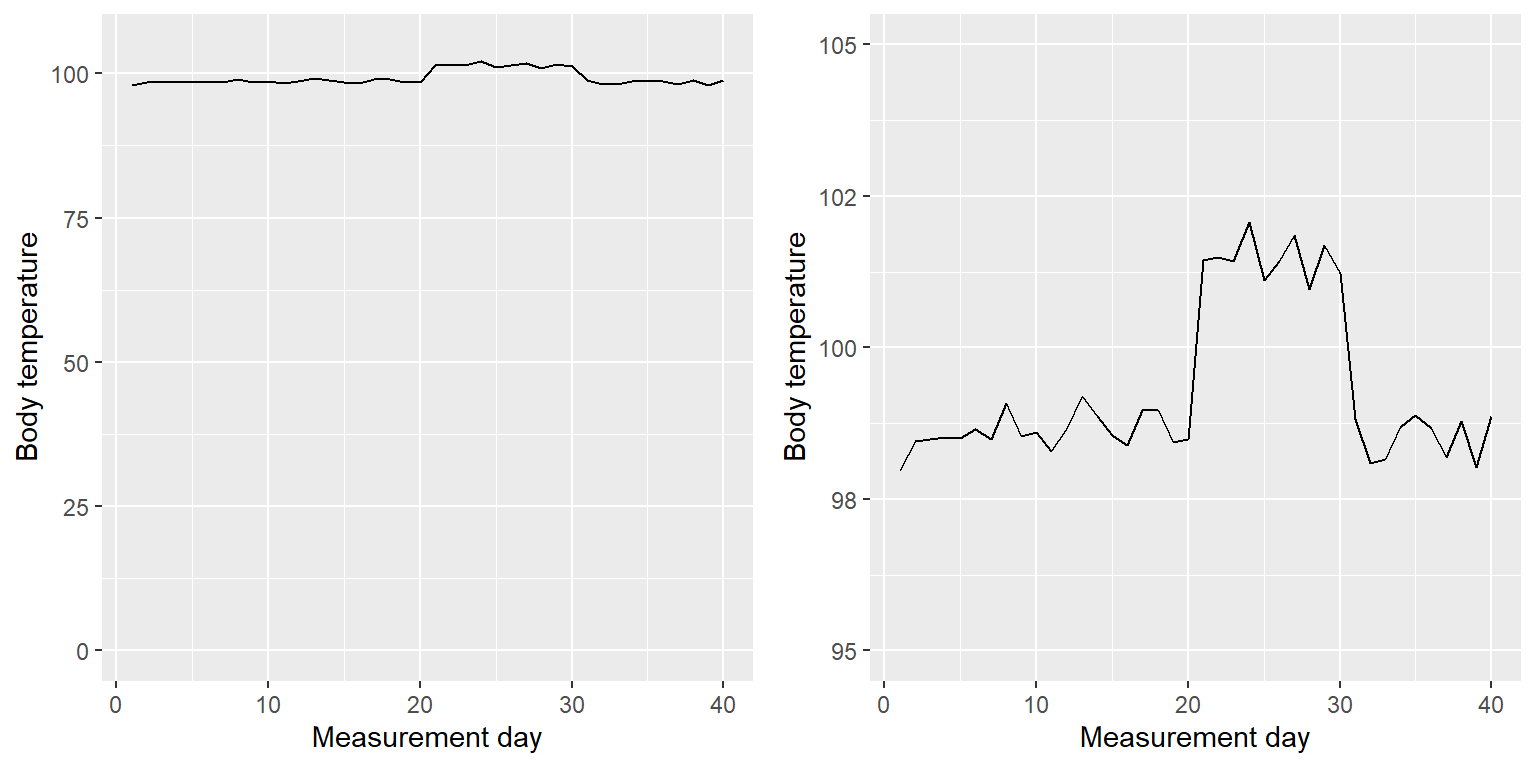
Figura 4.8: Temperatura corporal a lo largo del tiempo, graficada con o sin el punto cero en el eje Y.

Edward Tufte introdujo el concepto del factor de engaño (lie factor) para describir el grado en el cual las diferencias físicas en la visualización corresponden a la magnitud de las diferencias en los datos. Si una gráfica tiene un factor de engaño cercano a 1, entonces es una representación apropiada de los datos, pero si el factor de engaño es lejano a uno refleja una distorsión de los datos subyacentes.

El factor de engaño apoya el argumento de que uno siempre debería de incluir el punto cero en gráfico de barras en muchos casos. En la Figura 4.9 graficamos los mismos datos con y sin el cero en el eje Y. En el panel A, la diferencia proporcional del área de las dos barras es exactamente igual a la diferencia proporcional entre los valores (esto es, factor de engaño= 1), mientras que en el Panel B (donde el cero no está incluido) la diferencia proporcional en área entre las dos barras es aproximadamente 2.8 veces mayor que la diferencia proporcional de los valores, por lo tanto exagera visualmente el tamaño de la diferencia.

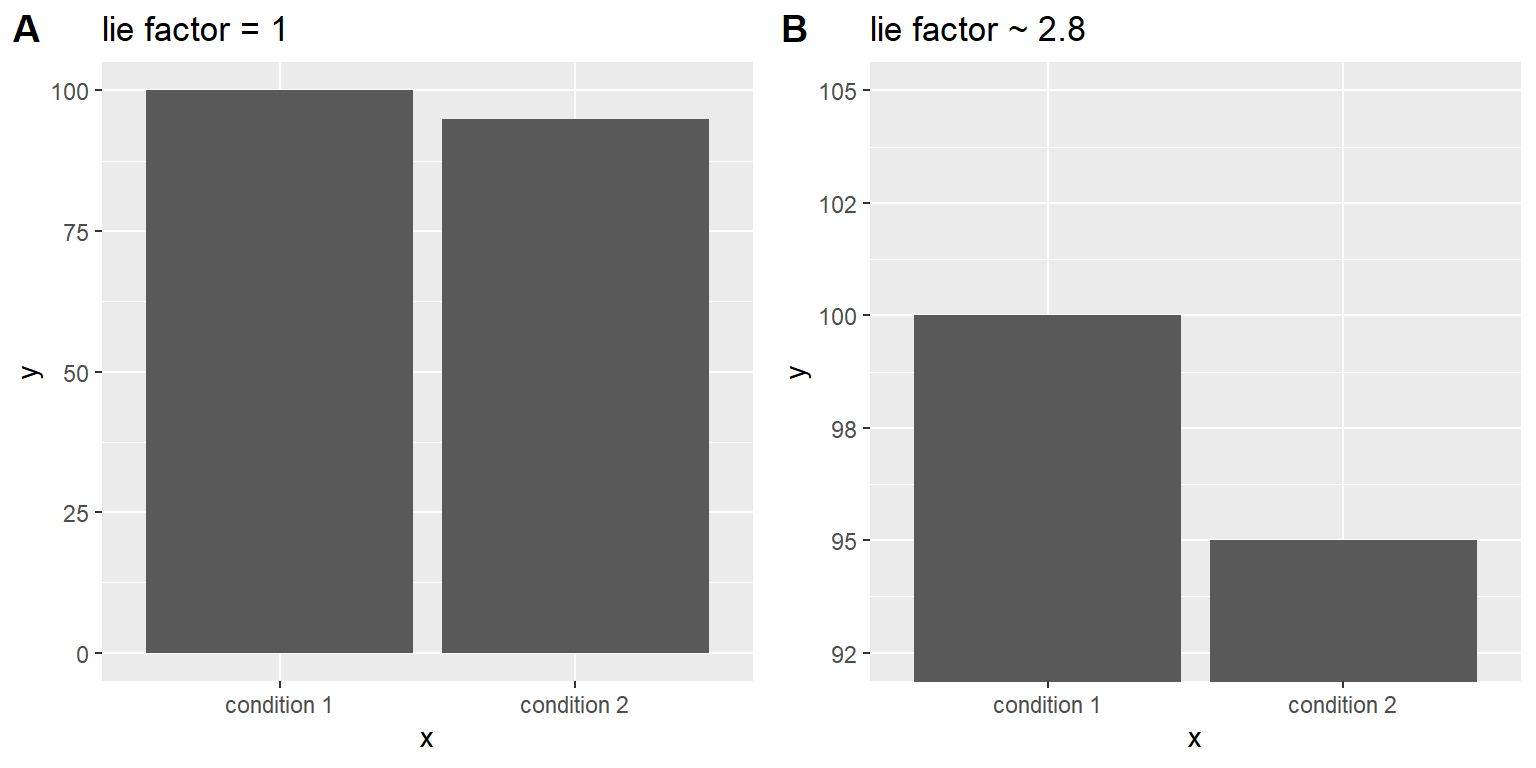
Figura 4.9: Dos gráficas de barra con sus factores de engaño respectivos.

4.3 Ajustarse a las limitaciones humanas

Les humanes tienen limitaciones perceptuales y cognitivas que pueden hacer ciertas visializaciones difíciles de entender. Siempre es importante tener esto en cuenta cuando se construye una visualización.

4.3.1 Limitaciones perceptuales

Una limitación perceptual importante que muchas personas (incluidas yo) sufren es daltonismo. Esto puede hacer muy difícil la percepción de la información en una figura (como la de la Figura 4.10) donde hay únicamente contraste de color entre los elementos pero no contraste de brillo. Siempre es útil utilizar elementos gráficos que difieran sustancialmente en brillo y/o textura en complemento al color. Existen también paletas de color amigables con daltónicxs disponibles para usarlas en muchas herramientas de visualización.

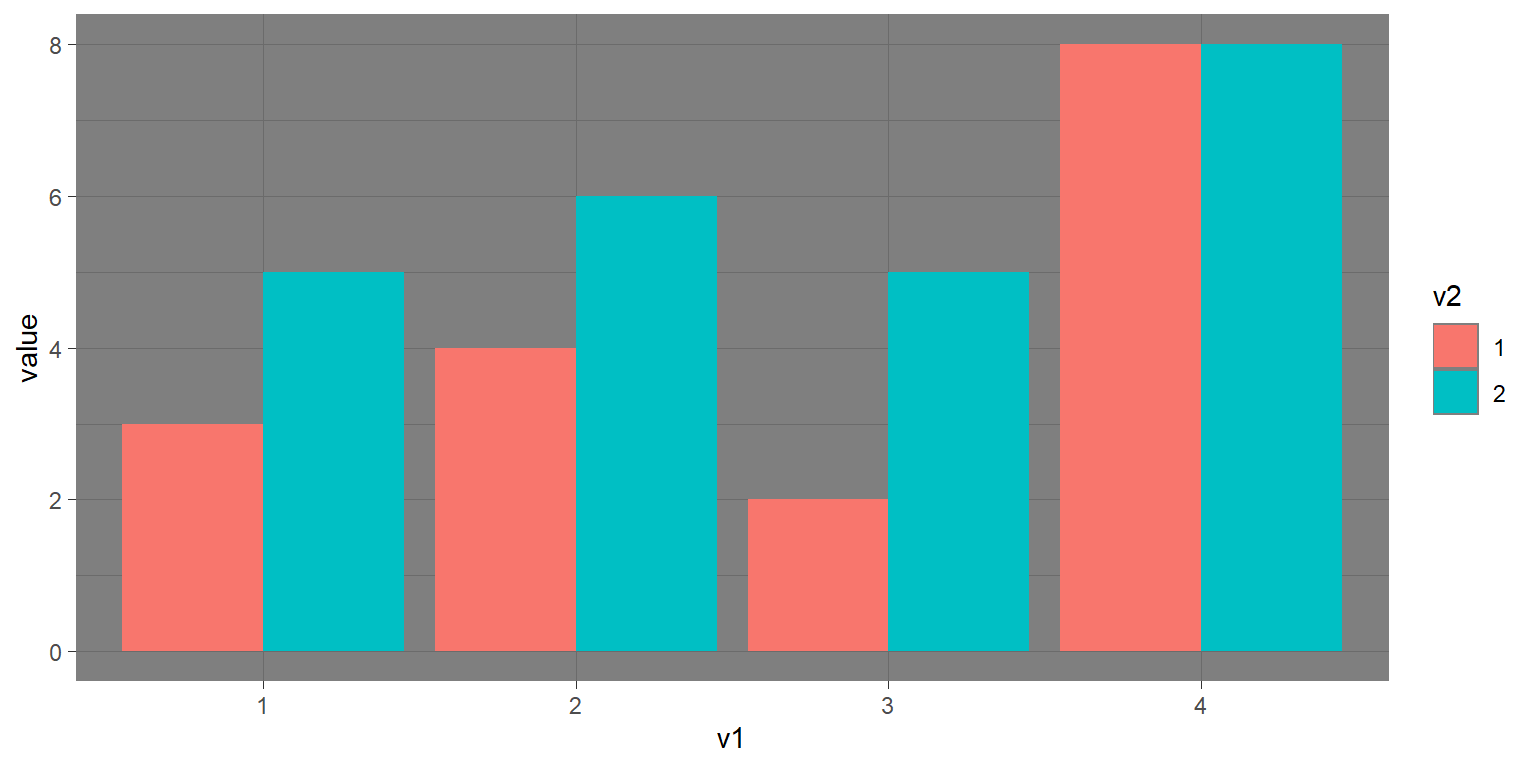
Figura 4.10: Ejemplo de una mala figura que depende únicamente en el contraste de color.

Incluso para personas con visión perfecta, hay algunas limitantes perceptuales que pueden hacer algunas gráficas ineficaces. Esta es una razón por la cual les estadístiques nunca usan gráficas circulares o de pastel: Puede ser muy difícil para les humanes percibir correctamente las diferencias en el volumen de las formas. La gráfica de pastel en la Figura 4.11 (presentando los mismos datos sobre afiliaciones religiosas que mostramos anteriormente) nos muestra qué tan complicado puede ser esto.

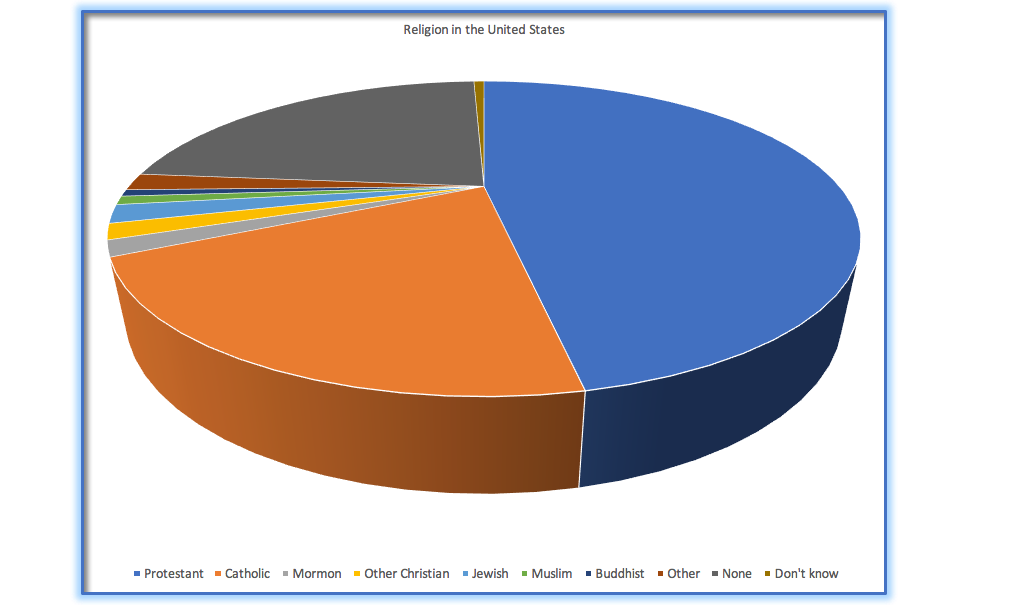
Figura 4.11: Un ejemplo de una gráfica de pastel (pay o sectores), enfatizando la dificultad para comprender el volumen relativo de las diferentes rebanadas de pastel.

Esta gráfica es terrible por varias razones. Primero, requiere distinguir un gran número de colores de parches muy pequeños en la parte inferior de la figura. Segundo, la perspectiva visual distorsiona los números relativos, tal como la rebanada de pastel para “Católica” que aparece mucho más grande que la rebanada para “Ninguna,” cuando en realidad el número para “Ninguna” es ligeramente mayor (22.8 vs 20.8 porciento), como es evidente en la Figura 4.6. Tercero, al separar la leyenda del gráfico, requiere que les lectores retengan información en su memoria de trabajo para poder mapear entre el gráfico y la leyenda y realizar muchas “búsquedas de tablas” para hacer coincidir continuamente las etiquetas de la leyenda con la visualización. Y, por último, utiliza texto que es demasiado pequeño, lo que hace que sea imposible leerlo sin hacer zoom.

Graficando los datos usando un enfoque más razonable (Figura 4.12), podemos ver el patrón mucho más claramente. Es posible que este gráfico no parezca tan llamativo como el gráfico circular generado con Excel, pero es una representación mucho más eficaz y precisa de los datos.

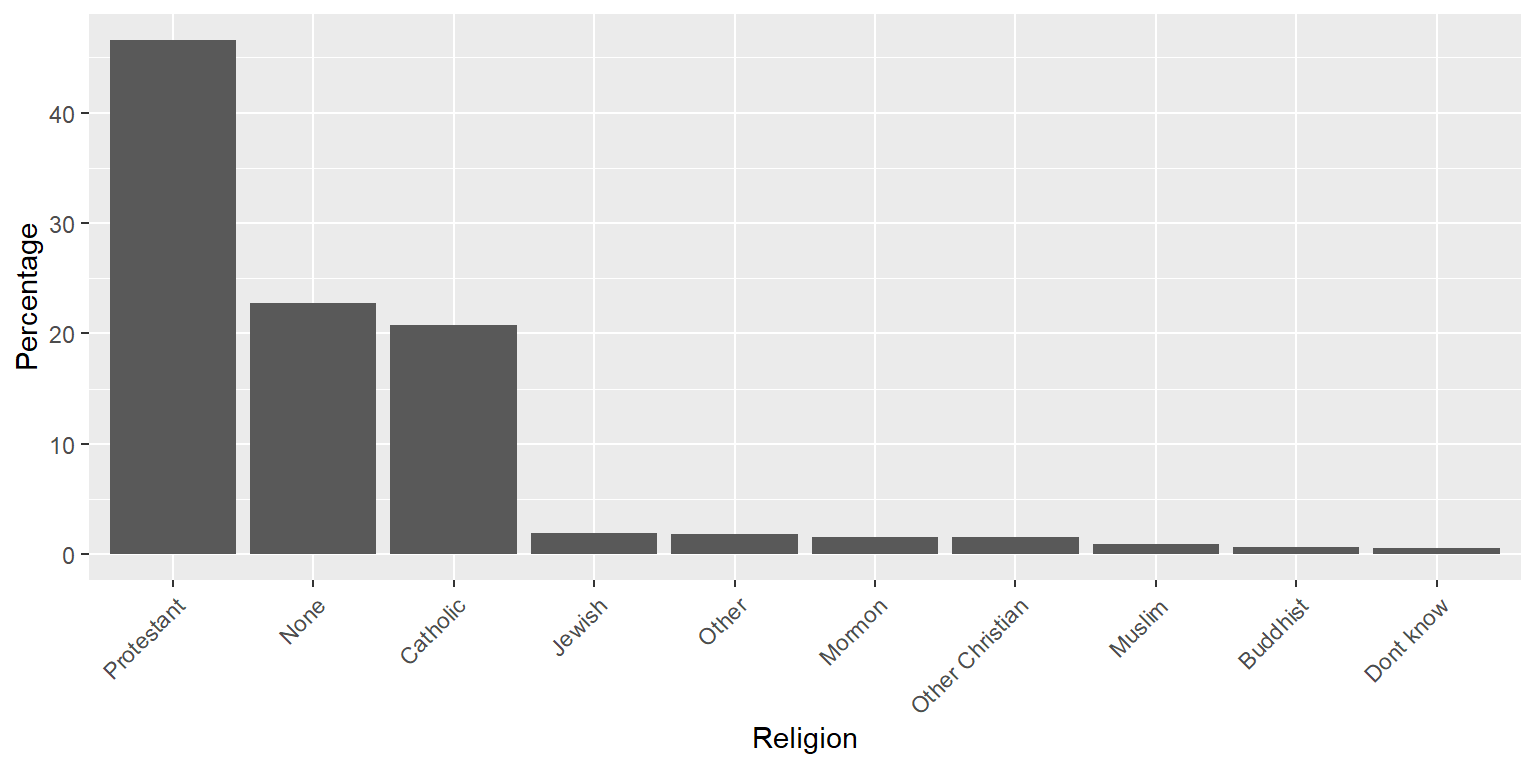
Figura 4.12: Una presentación más clara de los datos de afiliación religiosa (obtenido de http://www.pewforum.org/religious-landscape-study/).

Esta gráfica permite al espectador hacer comparaciones basadas en la longitud de las barras a lo largo de una escala común (el eje y). Los seres humanos tienden a ser más precisos al decodificar las diferencias en función de estos elementos perceptivos que en función del área o del color.

4.4 Corrigiendo otros factores

Comúnmente estamos interesades en graficar datos donde la variable de interés es afectada por otros factores aparte del que nos interesa. Por ejemplo digamos que queremos entender cómo el precio de la gasolina ha cambiado con el paso del tiempo. La figura 4.13 muestra datos históricos sobre el precio de la gasolina, graficado con o sin el ajuste de la inflación. Mientras que los datos sin ajuste muestran un gran incremento, los datos con ajuste muestran que es simplemente un reflejo de la inflación. Otros ejemplos donde se necesita ajustar los datos por otros factores incluye el tamaño de la población y datos obtenidos a través de diferentes temporadas.

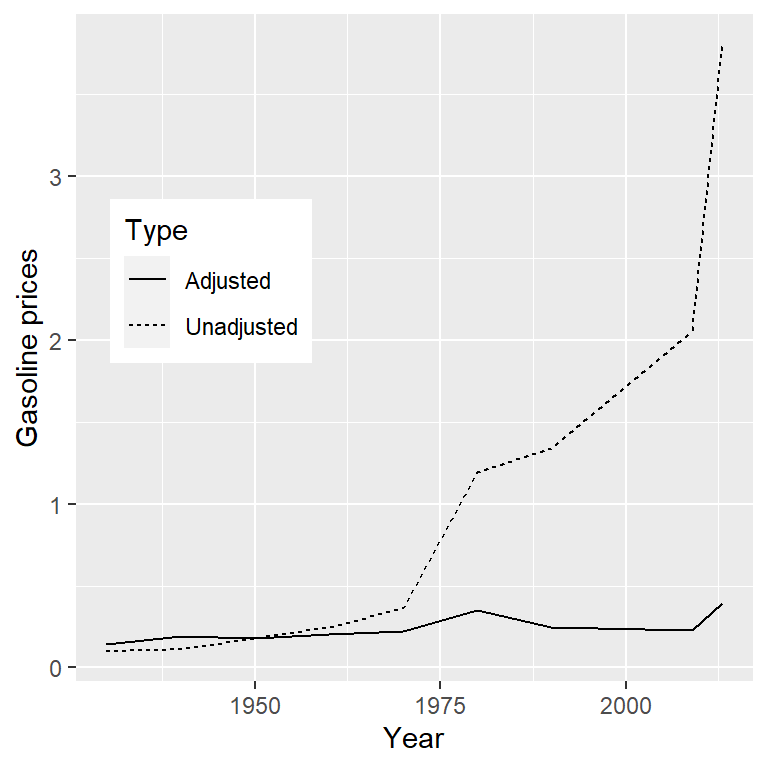
Figura 4.13: El precio de la gasolina en Estados Unidos de 1930 a 2013 (obtenido de http://www.thepeoplehistory.com/70yearsofpricechange.html) con o sin la corrección para inflación (basado en Consumer Price Index).

4.5 Objetivos de aprendizaje

Al terminar de leer este capítulo deberás de ser capaz de:

• Describir los principios que distinguen a las buenas y malas gráficas, y usarlos para identificar buenos y malos gráficos.
• Entender las limitaciones humanas que deben de ser consideradas para hacer gráficas eficaces.
• Prometer nunca crear una gráfica de pastel. Jamás.

4.6 Lecturas y videos sugeridos

• Fundamentals of Data Visualization, por Claus Wilke.
• Visual Explanations, por Edward Tufte.
• Visualizing Data, por William S. Cleveland.
• Graph Design for the Eye and Mind, por Stephen M. Kosslyn.
• How Humans See Data, por John Rauser .