Capitulo 12 Modelar relaciones categóricas

Hasta ahora hemos discutido los conceptos generales de la modelación estadística y de la prueba de hipótesis, y los hemos aplicado a algunos análisis simples; ahora nos enfocaremos a la pregunta de cómo modelar tipos particulares de relaciones en nuestros datos. En este capítulo nos enfocaremos en la modelación de relaciones categóricas, con lo cual queremos decir relaciones entre variables que son medidas de manera cualitativa. Estos datos son usualmente expresados en términos de conteos; esto es, para cada valor de la variable (o combinación de valores de múltiples variables), ¿cuántas observaciones toman ese valor? Por ejemplo, cuando contamos cuántas personas de cada licenciatura hay en nuestra clase, estamos ajustando un modelo categórico a nuestros datos.

12.1 Ejemplo: Dulces de colores

Digamos que compré una bolsa con 100 dulces, que está etiquetada diciendo que tiene 1/3 de chocolates, 1/3 de regaliz (licorice), y 1/3 de chicles. Cuando cuento los dulces en la bolsa, tengo los siguientes números: 30 chocolates, 33 de regaliz, y 37 chicles. Como me gusta el chocolate mucho más que el regaliz y los chicles, me siento ligeramente estafado y quisiera saber si esto fue sólo un accidente azaroso. Para responder esta pregunta, necesito saber: ¿Cuál es la probabilidad de que el conteo hubiera salido como salió si la verdadera probabilidad de cada tipo de dulce es realmente el promedio de una proporción de 1/3 de cada uno?

12.2 Prueba Ji-cuadrada de Pearson

La prueba Ji-cuadrada de Pearson (también conocida como chi-cuadrada, del inglés chi-squared) nos provee de una manera de probar si el conjunto de conteos observados difiere de algunos valores esperados en específico definidos por la hipótesis nula:

\[ \chi^2 = \sum_i\frac{(observado_i - esperado_i)^2}{esperado_i} \]

En el caso de nuestro ejemplo de los dulces, la hipótesis nula es que la proporción de cada tipo de dulce es igual. Para calcular el estadístico Ji-cuadrada, primero necesitamos proponer nuestros conteos esperados bajo la hipótesis nula: como la nula es que todos los conteos sean iguales, entonces estos valores esperados serán sólo el conteo total dividido entre las tres categorías (como se muestra en la Tabla 12.1). Luego tomamos la diferencia entre cada conteo observado y lo esperado bajo la hipótesis nula, lo elevamos al cuadrado, dividimos entre lo esperado por la nula, y los sumamos para obtener el estadístico Ji-cuadrada.

Tabla 12.1: Conteos observados, conteos esperados bajo la hipótesis nula, y las diferencias al cuadrado, en nuestros datos de los dulces.
Candy Type count nullExpectation squared difference
chocolate 30 33 11.11
licorice 33 33 0.11
gumball 37 33 13.44

El estadístico Ji-cuadrada para este análisis resulta en 0.74, que por sí mismo no es interpretable, porque depende del número de valores diferentes que fueron sumados en cojunto. Sin embargo, podemos aprovechar el hecho de que el estadístico Ji-cuadrada se distribuye de acuerdo a una distribución específica bajo la hipótesis nula, que es conocida como la distribución Ji-cuadrada. Esta distribución es definida por la suma de los cuadrados de un conjunto de variables aleatorias normales estándares; tiene un número de grados de libertad que es igual al número de variables que están siendo sumadas. La forma de la distribución depende del número de grados de libertad. El panel izquierdo de la Figura 12.1 muestra ejemplos de la distribución de diferentes grados de libertad.

Izquierda: Ejemplos de una distribución Ji-cuadrada para varios grados de libertad. Derecha: Simulación de la suma de cuadrados de variables aleatorias normales. El histograma está basado en la suma de cuadrados de 50,000 conjuntos de 8 variables normales aleatorias; la línea punteada muestra los valores de la distribución ji-cuadrada teórica con 8 grados de libertad.

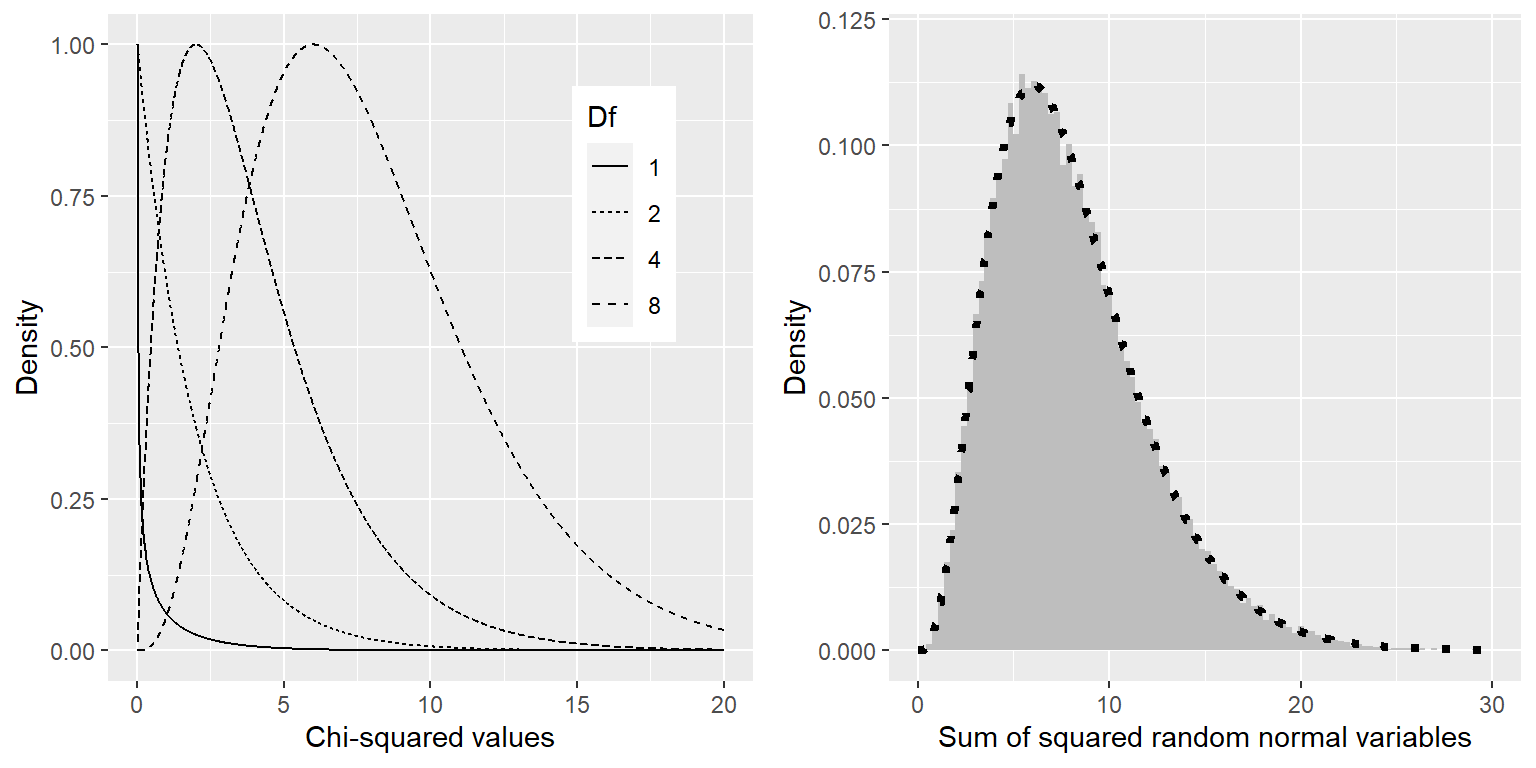
Figura 12.1: Izquierda: Ejemplos de una distribución Ji-cuadrada para varios grados de libertad. Derecha: Simulación de la suma de cuadrados de variables aleatorias normales. El histograma está basado en la suma de cuadrados de 50,000 conjuntos de 8 variables normales aleatorias; la línea punteada muestra los valores de la distribución ji-cuadrada teórica con 8 grados de libertad.

Verifiquemos que la distribución ji-cuadrada describe con exactitud la suma de cuadrados de un conjunto de variables aleatorias normales estándares, usando una simulación. Para hacer esto, repetidamente tomamos un conjunto de 8 números aleatorios, y sumamos cada conjunto después de haberlos elevado al cuadrado. El panel derecho de la Figura 12.1 muestra que la distribución teórica coincide cercanamente con los resultados de la simulación que repetidamente suma los cuadrados de un conjunto de variables normales aleatorias.

Para el ejemplo de los dulces, podemos calcular la probabilidad de nuestro valor ji-cuadrada observado de 0.74 bajo la hipótesis nula de que la frecuencia de los diferentes tipos de dulces sería igual. Usamos una distribución ji-cuadrada con grados de libertad igual a k - 1 (donde k = número de categorías) porque perdimos un grado de libertad cuando calculamos la media para generar los valores esperados. El valor p resultante (P(Chi-squared) > 0.74 = 0.691) muestra que los conteos observados de dulces no son particularmente sorprendentes basados en las proporciones que menciona la etiqueta de la bolsa de dulces, y no rechazaríamos la hipótesis nula de proporciones iguales.

12.3 Tablas de contingencia y la prueba de dos vías

Otra manera en que frecuentemente usamos la prueba ji-cuadrada es para preguntar si dos variables categóricas están relacionadas una con la otra. Como un ejemplo más realista, tomemos la pregunta de si un conductor negro es más probable que sea revisado cuando un oficial de policía le pide orillarse, comparado con un conductor blanco. El Stanford Open Policing Project (https://openpolicing.stanford.edu/) ha estudiado esto, y provee datos que podemos usar para analizar esta pregunta. Usaremos los datos del estado de Connecticut porque es un estado más pequeño y por lo tanto más fácil de analizar.

La manera estándar de representar datos de un análisis categórico es a través de una tabla de contingencia, que representa el número o la proporción de observaciones que cayeron en cada posible combinación de valores de cada una de las variables. La Tabla 12.2 muestra la tabla de contingencia para los datos de las revisiones policíacas. También puede ser útil armar la tabla de contingencia usando proporciones en lugar de números crudos, porque son más fáciles de comparar visualmente, así que incluimos ambos números absolutos y relativos aquí.

Tabla 12.2: Tabla de contingencia para los datos de revisiones policíacas.
searched Black White Black (relative) White (relative)
FALSE 36244 239241 0.13 0.86
TRUE 1219 3108 0.00 0.01

La prueba ji-cuadrada de Pearson nos permite probar si las frecuencias observadas son diferentes de las frecuencias esperadas, por lo que necesitamos determinar cuáles frecuencias se esperarían en cada celda si las revisiones y la raza no estuvieran relacionadas – es decir, si fueran independientes. Recuerda del capítulo de probabilidad que si X y Y son independientes, entonces:

\[ P(X \cap Y) = P(X) * P(Y) \] Esto es, la probabilidad conjunta bajo la hipótesis nula de independencia es simplemente la multiplicación de las probabilidades marginales de cada variable individual. Las probabilidades marginales son simplemente las probabilidades de que ocurra cada evento sin importar los otros eventos. Podemos calcular estas probabilidades marginales, y luego multiplicarlas juntas para obtener las proporciones esperadas bajo la hipótesis de independencia.

Black White
Not searched P(NS)*P(B) P(NS)*P(W) P(NS)
Searched P(S)*P(B) P(S)*P(W) P(S)
P(B) P(W)
Tabla 12.3: Resumen de la tabla de contingencia de 2 vías para los datos de revisiones policíacas.
searched driver_race n expected stdSqDiff
FALSE Black 36244 36884 11.1
TRUE Black 1219 579 706.3
FALSE White 239241 238601 1.7
TRUE White 3108 3748 109.2

Luego calculamos el estadístico ji-cuadrada, que resulta igual a 828.3. Para calcular el valor p, necesitamos comparar este valor con la distribución ji-cuadrada nula para poder determinar qué tan extremo es nuestro valor ji-cuadrada comparado con nuestras expectativas bajo la hipótesis nula. Los grados de libertad para esta distribución son \(gl = (nFilas - 1) * (nColumnas - 1)\) (en inglés: \(df = (nRows - 1) * (nColumns - 1)\), nota que \(df\) = \(gl\)) - por lo que, para una tabla 2X2 como la que tenemos aquí, \(gl = (2-1)*(2-1)=1\). La intuición aquí es que el calcular las frecuencias esperadas requiere que usemos tres valores: el número total de observaciones y la probabilidad marginal para cada una de las dos variables. Por lo que, una vez que esos valores con calculados, sólo hay un número que es libre de variar, por lo que sólo hay un grado de libertad. Dado esto, podemos calcular el valor p para el estadístico ji-cuadrada, el cual termina siendo tan cercano a cero como se podría obtener: \(3.79 \times 10^{-182}\). Esto muestra que los datos observados serían altamente improbables si no hubiera realmente una relación entre raza y revisiones policíacas, y por lo tanto debemos rechazar la hipótesis nula de independencia.

También podemos realizar esta prueba fácilmente usando nuestro software estadístico:

## 
##  Pearson's Chi-squared test
## 
## data:  summaryDf2wayTable and 1
## X-squared = 828, df = 1, p-value <2e-16

12.4 Residuales estandarizados (standardized residuales)

Cuando encontramos un efecto significativo con la prueba ji-cuadrada, esto nos dice que los datos son improbables bajo la hipótesis nula, pero no nos dice cómo difieren los datos. Para obtener un insight más profundo sobre cómo los datos difieren de lo que esperaríamos bajo la hipótesis nula, podemos examinar los residuales del modelo, que reflejan la desviación que tuvieron los datos (i.e., las frecuencias observadas) del modelo (i.e., las frecuencias esperadas) en cada celda. En lugar de ver los residuales crudos (que variarán simplemente dependiendo del número de observaciones en los datos), es más común observar los residuales estandarizados (a veces llamados residuales de Pearson), que se calculan como sigue:

\[ residuales\ estandarizados_{ij} = \frac{observados_{ij} - esperados_{ij}}{\sqrt{esperados_{ij}}} \] donde \(i\) y \(j\) son los índices de los renglones/filas y las columnas, respectivamente.

La Tabla 12.4 muestra estos valores para los datos de las revisiones policíacas. Estos residuales estandarizados pueden interpretarse como valores Z – en este caso, vemos que el número de revisiones para las personas negras son sustancialmente mayores que los esperados basados en independencia, y el número de revisiones para las personas blancas son sustancialmente menores que las esperadas. Esto nos provee del contexto que necesitamos para interpretar el resultado significativo de la ji-cuadrada.

Tabla 12.4: Resumen de los residuales estandarizados de los datos de revisiones policíacas.
searched driver_race Standardized residuals
FALSE Black -3.3
TRUE Black 26.6
FALSE White 1.3
TRUE White -10.4

12.5 Razones de posibilidades (odds ratios)

También podemos representar la probabilidad relativa de los diferentes resultados en la tabla de contingencia usando las razones de posibilidades (odds ratios) que presentamos en capítulos anteriores, para poder entender mejor la magnitud del efecto. Primero, representamos las posibilidades (odds) de ser revisado de cada raza, luego calculamos su razón:

\[ odds_{searched|black} = \frac{N_{searched\cap black}}{N_{not\ searched\cap black}} = \frac{1219}{36244} = 0.034 \]

\[ odds_{searched|white} = \frac{N_{searched\cap white}}{N_{not\ searched\cap white}} = \frac{3108}{239241} = 0.013 \] \[ odds\ ratio = \frac{odds_{searched|black}}{odds_{searched|white}} = 2.59 \]

La razón de posibilidades muestra que las posibilidades de ser revisado son 2.59 veces mayores para conductores negros versus conductores blancos, basados en esta base de datos.

12.6 Factores de Bayes

Discutimos los factores de Bayes en el capítulo anterior sobre estadística Bayesiana – podrás recordar que representan la razón de las probabilidades (likelihood) de los datos bajo cada una de las dos hipótesis:

\[ K = \frac{P(data|H_A)}{P(data|H_0)} = \frac{P(H_A|data)*P(H_A)}{P(H_0|data)*P(H_0)} \] Podemos calcular el factor de Bayes para los datos de las revisiones policiacas usando nuestro software estadístico:

## Bayes factor analysis
## --------------
## [1] Non-indep. (a=1) : 1.8e+142 ±0%
## 
## Against denominator:
##   Null, independence, a = 1 
## ---
## Bayes factor type: BFcontingencyTable, independent multinomial

Esto nos muestra que la evidencia en favor de una relación entre la raza de los conductores y las revisiones policíacas en este conjunto de datos es extremadamente fuerte — \(1.8 * 10^{142}\) es tan cercano a infinito como podemos imaginarnos llegar a obtener en estadística.

12.7 Análisis categóricos más allá de la tabla 2 X 2

El análisis categórico también puede aplicarse a tablas de contingencia donde haya más de dos categorías para cada variables.

Por ejemplo, veamos los datos de NHANES y comparemos la variable Depressed que registra el “número de días auto-reportado donde el participante se sintió bajo de ánimo, deprimido, o desesperanzado.” Esta variable está codificada como None, Several, o Most. Hagamos la prueba de si esta variable está relacionada con la variable SleepTrouble que registra si la persona ha reportado problemas de sueño a su doctor.

Tabla 12.5: Relación entre depresión y problemas de sueño en la base de datos NHANES.
Depressed NoSleepTrouble YesSleepTrouble
None 2614 676
Several 418 249
Most 138 145

Simplemente observando estos datos podemos decir que es probable que haya una relación entre estas dos variables; notablemente, mientras que el total de personas con problemas de sueño es mucho menor que aquellas sin estos problemas, para aquellas personas que reportaron sentirse deprimidas la mayoría de los días el número de personas con problemas de sueño es mayor que las que no tienen problemas de sueño. Podemos cuantificar esto directamente usando la prueba ji-cuadrada:

## 
##  Pearson's Chi-squared test
## 
## data:  depressedSleepTroubleTable
## X-squared = 191, df = 2, p-value <2e-16

Esta prueba muestra que hay una relación fuerte entre depresión y problemas de sueño. También podemos calcular el factor de Bayes para cuantificar la fuerza de la evidencia a favor de la hipótesis alternativa:

## Bayes factor analysis
## --------------
## [1] Non-indep. (a=1) : 1.8e+35 ±0%
## 
## Against denominator:
##   Null, independence, a = 1 
## ---
## Bayes factor type: BFcontingencyTable, joint multinomial

Aquí podemos ver que el factor de Bayes es muy grande (\(1.8 * 10^{35}\)), mostrando que la evidencia a favor de la relación entre depresión y problemas de sueño es muy fuerte.

12.8 Cuídate de la paradoja de Simpson

Las tablas de contingencia anteriores representan resúmenes de números grandes de observaciones, pero los resúmenes pueden ser engañosos. Veamos un ejemplo de baseball. La tabla debajo muestra los datos de bateo (hits/turnos al bate y bateo promedio) para Derek Jeter y David Justice sobre los años 1995-1997:

Player 1995 1996 1997 Combined
Derek Jeter 12/48 .250 183/582 .314 190/654 .291 385/1284 .300
David Justice 104/411 .253 45/140 .321 163/495 .329 312/1046 .298

Si miras cuidadosamente, verás que algo raro está sucediendo: En cada año individual Justice tuvo un promedio de bateo mayor a Jeter, pero cuando combinamos los datos a lo largo de los tres años, ¡el promedio de Jeter es finalmente mayor que el de Justice! Esto es un ejemplo de un fenómeno conocido como la paradoja de Simpson, en el cual un patrón que está presente en un conjunto combinado de datos puede no estar presente en cualquier de los subconjuntos de los mismos datos. Esto ocurre cuando hay otra variable que puede estar cambiando a través de los diferentes subconjuntos – en este caso, el número de turnos al bate varía en los diferentes años, donde Justice tuvo muchos más turnos al bate en 1995 (cuando el promedio de hits era bajo). Nos referimos a esto como una variable oculta (lurking variable), y es siempre importante estar atentos a tales variables cada vez que examinemos datos categóricos.

12.9 Objetivos de aprendizaje

  • Describir el concepto de una tabla de contingencia para datos categóricos.
  • Describir el concepto de la prueba ji-cuadrada para una asociación y calcularla para una tabla de contingencia.
  • Describir la paradoja de Simpson y por qué es importante para análisis de datos categóricos.

12.10 Lecturas adicionales