Capitulo 10 Cuantificar efectos y diseñar estudios

En el capítulo anterior discutimos cómo podemos usar los datos para probar hipótesis. Esos métodos proporcionaron una respuesta binaria: o rechazamos o no rechazamos la hipótesis nula. Sin embargo, este tipo de decisión pasa por alto un par de cuestiones importantes. Primero, nos gustaría saber cuánta incertidumbre tenemos sobre la respuesta (independientemente de la dirección que tome). Además, a veces no tenemos una hipótesis nula clara, por lo que nos gustaría ver qué rango de estimaciones son consistentes con los datos. En segundo lugar, nos gustaría saber qué tan grande es el efecto en realidad, ya que como vimos en el ejemplo de pérdida de peso en el capítulo anterior, un efecto estadísticamente significativo no es necesariamente un efecto importante prácticamente.

En este capítulo analizaremos métodos para abordar estas dos preguntas: intervalos de confianza para proporcionar una medida de nuestra incertidumbre acerca de nuestras estimaciones y tamaños del efecto para proporcionar una forma estandarizada de comprender qué tan grandes son los efectos. También discutiremos el concepto de poder estadístico que nos dice con cuánta probabilidad encontraremos algún efecto verdadero que realmente exista.

10.1 Intervalos de confianza

Hasta ahora en el libro nos hemos enfocado en estimar un estadístico de un solo valor. Por ejemplo, digamos que queremos estimar el peso medio de los adultos en el conjunto de datos de NHANES, por lo que tomamos una muestra del conjunto de datos y estimamos la media. En este ejemplo, el peso medio tiene 79.92 kilogramos. Nos referimos a esto como un punto estimado ya que nos provee con un simple número para describir nuestra estimación del parámetro poblacional. Como sea, sabemos de nuestra discusión anterior sobre el error de muestreo que hay cierta incertidumbre acerca de este estimado, que es descrito como error estándar. También recordarás que el error estándar es determinado por dos componentes: la desviación estándar de la población (que es el numerador), y la raíz cuadrada del tamaño de la muestra (que es el denominador). La desviación estándar de la población es un parámetro generalmente desconocido, pero fijo que no está bajo nuestro control, mientras que el tamaño de la muestra está bajo nuestro control. De este modo, podemos disminuir nuestra incertidumbre acerca del estimado aumentando nuestro tamaño de muestra – hasta el límite del tamaño de dicha población, al punto que no hay incertidumbre del todo porque podemos calcular el parámetro poblacional directamente de los datos de la población entera.

Frecuentemente querremos tener una manera más directa de describir nuestra incertidumbre acerca de un estadístico estimado, lo que podemos lograr usando un intervalo de confianza (confidence interval). La mayoría de las personas están familiarizadas con los intervalos de confianza a partir de la idea de un “margen de error” en encuestas políticas. Estas encuestas usualmente intentan proveer una respuesta que es precisa dentro de un +/- 3%. Por ejemplo, cuando se estima que un candidato gane la elección por 9 puntos porcentuales con un margen de error de 3, el porcentaje por el cual va a ganar se estima que estará dentro de 6-12 puntos porcentuales. En estadística nos referimos a este tipo de rango de valores como un intervalo de confianza, el cual provee un rango de valores para nuestro parámetro estimado que son consistentes con los datos de nuestra muestra, en lugar de sólo darnos un solo valor estimado basado en los datos. Entre más amplio sea el intervalo de confianza, mayor incertidumbre tendremos acerca de nuestro parámetro estimado.

Los intervalos de confianza son notoriamente confusos, primeramente porque no significan lo que intuitivamente pensaríamos que significan. Si te dijera que he calculado un “intervalo de confianza al 95%” de mi estadística, entonces parecería natural pensar que tendríamos 95% de confianza en que el verdadero valor del parámetro estará dentro de este intervalo. Sin embargo, como veremos a través del curso, los conceptos en estadística regularmente no significan lo que creemos que deberían significar. En el caso de los intervalos de confianza, no podemos interpretarlos en esta manera porque el parámetro poblacional tiene un valor fijo – está o no está en el intervalo, por lo que no tiene sentido hablar de la probabilidad de que eso ocurra. Jerzy Neyman, el inventor del intervalo de confianza, dijo:

“El parámetro es una constante desconocida y no se puede hacer ninguna declaración de probabilidad sobre su valor.” (J. Neyman 1937)

En lugar de eso, tenemos que ver al procedimiento del intervalo de confianza desde el mismo punto de vista con el que vimos la prueba de hipótesis: Un procedimiento que en el largo plazo nos permitirá hacer enunciados correctos con una probabilidad particular. Por lo tanto, la interpretación correcta del intervalo de confianza del 95% es que es un intervalo que contendrá la media poblacional verdadera el 95% del tiempo y, de hecho, podemos confirmarlo usando simulación, como verás más abajo.

El intervalo de confianza para la media se calcula como:

\[ CI = \text{point estimate} \pm \text{critical value} * \text{standard error} \]

donde el valor crítico es determinado por la distribución muestral de la medida estimada. La pregunta importante, entonces, es cómo obtener nuestra estimación para esa distribución muestral.

10.1.1 Intervalos de confianza usando la distribución normal

Si sabemos la desviación estándar de la población, entonces podemos usar la distribución normal para calcular un intervalo de confianza. Usualmente no la sabemos, pero para nuestro ejemplo en el conjunto de datos NHANES sí sabemos, puesto que tomamos a la base de datos completa como si fuera la población (es 21.3 para el peso).

Digamos que queremos calcular un intervalo de confianza de 95% para la media. El valor crítico entonces serían los valores de la distribución normal estándar que capturen el 95% de la distribución; estos son simplemente 2.5 de percentil y el 97.5 percentil de la distribución, el cual podemos calcular usando un software estadístico, y resulta un valor de \(\pm 1.96\). Por lo tanto, el intervalo de confianza para la media (\(\bar{X}\)) es: \[ CI = \bar{X} \pm 1.96*SE \]

Usando la media estimada de nuestra muestra (79.92) y la conocida desviación estándar de la población podemos calcular el intervalo de confianza de [77.28,82.56].

10.1.2 Intervalos de confianza utilizando la distribución t

Como se indicó anteriormente, si conociéramos la desviación estándar de la población, podríamos usar la distribución normal para calcular nuestros intervalos de confianza. Sin embargo, en general no lo sabemos, en cuyo caso la distribución t es más apropiada como distribución de muestreo. Recuerde que la distribución t es ligeramente más amplia que la distribución normal, especialmente para muestras más pequeñas, lo que significa que los intervalos de confianza serán ligeramente más amplios de lo que serían si estuviéramos usando la distribución normal. Esto incorpora la incertidumbre adicional que surge cuando estimamos parámetros basados en muestras pequeñas.

Podemos calcular el intervalo de confianza al 95% en una manera similar al de la distribución normal en el ejemplo de arriba, pero el valor crítico es determinado por el percentil 2.5 y por el 97.5 percentil de la distribución t con los grados apropiados de libertad. Por lo tanto el intervalo de confianza para la media (\(\bar{X}\)) es:

\[ CI = \bar{X} \pm t_{crit}*SE \]

donde \(t_{crit}\) es el valor crítico de t. Para el ejemplo del peso en NHANES (con una muestra de tamaño 250), el intervalo de confianza sería de 79.92 +/- 1.97 * 1.41 [77.15 - 82.69].

Recuerde que esto no nos dice nada acerca de la probabilidad de que el valor real de la población caiga dentro de este intervalo, ya que es un parámetro fijo (que sabemos que es 81.77 porque tenemos a toda la población en este caso) y cae o no dentro de este intervalo específico (en este caso, sí). En cambio, nos dice que a largo plazo, si calculamos el intervalo de confianza utilizando este procedimiento, el 95% de las veces ese intervalo de confianza capturará el parámetro de población real.

Podemos ver esto usando la base de datos NHANES como si fuera nuestra población; en este caso, sabemos el verdadero valor del parámetro poblacional, por lo que podemos ver qué tan frecuentemente el intervalo de confianza termina capturando ese valor a lo largo de muchas diferentes muestras. La Figura 10.1 muestra los intervalos de confianza para las medias estimadas del peso calculadas para 100 muestras obtenidas de la base de datos NHANES. De estos, 95 capturaron la verdadera media poblacional del peso, mostrando que el procedimiento del intervalo de confianza funcionó como debía.

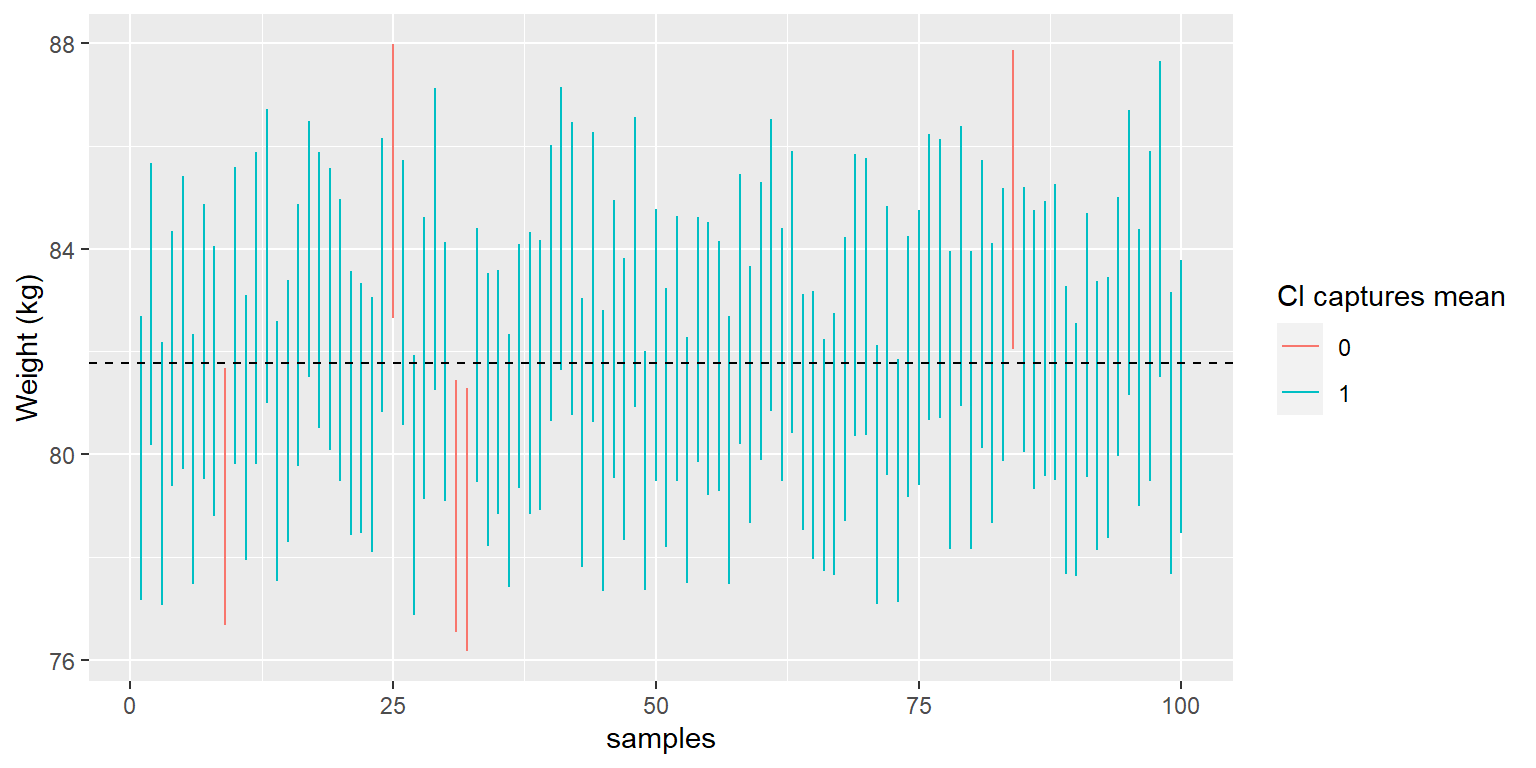
Figura 10.1: Las muestras fueron obtenidas repetidamente de la base de datos NHANES, y el intervalo de confianza de la media al 95% fue calculado para cada muestra. Los intervalos mostrados en rojo no capturaron la media poblacional verdadera (mostrada con la línea punteada).

10.1.3 Intervalos de confianza y tamaño de muestra

Debido a que el error estándar disminuye con el tamaño de la muestra, el intervalo de confianza debería hacerse más estrecho a medida que aumenta el tamaño de la muestra, proporcionando límites progresivamente más estrechos en nuestra estimación. La figura 10.2 muestra un ejemplo de cómo cambiaría el intervalo de confianza en función del tamaño de la muestra para el ejemplo del peso. A partir de la figura es evidente que el intervalo de confianza se vuelve cada vez más estrecho a medida que aumenta el tamaño de la muestra, pero el aumento de las muestras proporciona rendimientos decrecientes, en consonancia con el hecho de que el denominador del término del intervalo de confianza es proporcional a la raíz cuadrada del tamaño de la muestra.

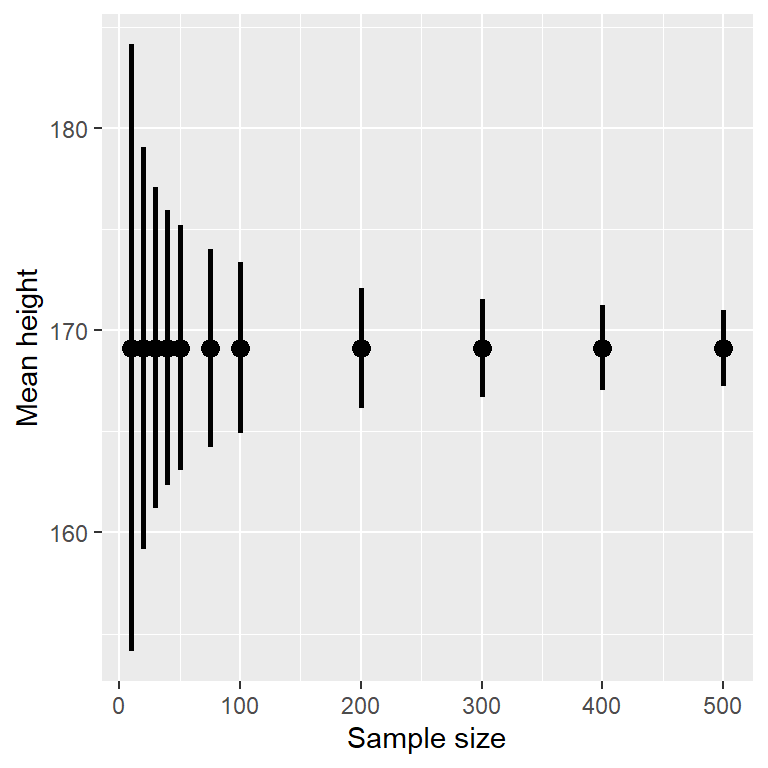
Figura 10.2: Ejemplo del efecto de tamaño de muestra en la amplitud del intevalo de confianza para la media.

10.1.4 Calcular el intervalo de confianza utilizando “bootstrap”

En algunos casos, no podemos asumir la normalidad o no conocemos la distribución muestral del estadístico. En estos casos, podemos usar el bootstrap (que presentamos en el Capítulo 8). Como recordatorio, el bootstrap implica volver a muestrear repetidamente los datos con reemplazo, y luego usar la distribución de la estadística calculada en esas muestras como un sustituto de la distribución muestral de la estadística. Estos son los resultados cuando usamos el la función integrada en R para calcular el intervalo de confianza para el peso en nuestra muestra NHANES:

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bs, type = "perc")
## 
## Intervals : 
## Level     Percentile     
## 95%   (78, 84 )  
## Calculations and Intervals on Original Scale

Estos valores son bastante cercanos a los valores obtenidos usando la distribución t antedicha, pero no exactamente iguales.

10.1.5 Relación de los intervalos de confianza con la prueba de hipótesis

Existe una estrecha relación entre los intervalos de confianza y las pruebas de hipótesis. En particular, si el intervalo de confianza no incluye la hipótesis nula, entonces la prueba estadística asociada sería estadísticamente significativa. Por ejemplo, si se está probando si la media de una muestra es mayor que cero con \(\alpha = 0.05\), simplemente puede verificarse si el cero está contenido dentro del intervalo de confianza del 95% para la media.

–> Las cosas se complican si queremos comparar las medias de dos condiciones (Schenker and Gentleman 2001). Hay un par de situaciones que están claras. Primero, si cada media está contenida dentro del intervalo de confianza de la otra media, entonces definitivamente no hay diferencia significativa en el nivel de confianza elegido. En segundo lugar, si no hay superposición entre los intervalos de confianza, ciertamente hay una diferencia significativa en el nivel elegido; de hecho, esta prueba es sustancialmente conservadora, de modo que la tasa de error real será menor que el nivel elegido. Pero, ¿qué pasa con el caso en el que los intervalos de confianza se superponen entre sí pero no contienen la media del otro grupo? En este caso, la respuesta depende de la variabilidad relativa de las dos variables y no hay una respuesta general. Sin embargo, en general, se debe evitar el uso de “medir a simple vista” para los intervalos de confianza superpuestos.

10.2 Tamaño de efecto (effect sizes)

“La significatividad estadística es lo menos interesante de los resultados. Debes describir los resultados en términos de medidas de magnitud, no solo si un tratamiento afecta a las personas, sino cuánto las afecta.” Gene Glass, citado en (Sullivan and Feinn 2012).

En el capítulo anterior, discutimos la idea de que la significación estadística no necesariamente refleja significación práctica. Para discutir la importancia práctica, necesitamos una forma estándar de describir el tamaño de un efecto en términos de los datos reales, a los que nos referimos como tamaño del efecto (effect size). En esta sección presentaremos el concepto y discutiremos varias formas en que se pueden calcular los tamaños del efecto.

El tamaño del efecto es una medida estandarizada que compara el tamaño de algún efecto estadístico con una cantidad de referencia, como la variabilidad de la estadística. En algunos campos de la ciencia y la ingeniería, esta idea se conoce como “relación señal/ruido.” Hay muchas formas diferentes de cuantificar el tamaño del efecto, que dependen de la naturaleza de los datos.

10.2.1 D de Cohen

Una de las medidas más comunes de tamaño de efectos es conocida como la d de Cohen, nombrada en honor al estadístico Jacob Cohen (quien es más famoso por su trabajo de 1994 “El mundo es redondo (p < .05)”). Es usada para cuantificar la diferencia entre dos medias, en términos de su desviación estándar:

\[ d = \frac{\bar{X}_1 - \bar{X}_2}{s} \]

donde \(\bar{X}_1\) y \(\bar{X}_2\) son las medias de los dos grupos, y \(s\) es la desviación estándar agrupada (la cual es una combinación de las desviaciones estándar de las dos muestras, ponderadas por sus tamaños de muestra):

\[ s = \sqrt{\frac{(n_1 - 1)s^2_1 + (n_2 - 1)s^2_2 }{n_1 +n_2 -2}} \] donde \(n_1\) y \(n_2\) son tamaños de muestra y \(s^2_1\) y \(s^2_2\) son las desviaciones estándar de los dos grupos, respectivamente. Nótese que esto es muy similar en espíritu al estadístico t — la diferencia principal es que el denominador en la estadística está basada en el error estándar de la media, mientras que el denominador en la D de Cohen está basada en la desviación estándar de los datos. Esto significa que mientras que la estadística t va a crecer conforme al tamaño de la muestra aumente, el valor de la D de Cohen se mantendrá igual.

Tabla 10.1: Interpetation of Cohen’s D

D	Interpretation
0.0 - 0.2	neglibible
0.2 - 0.5	small
0.5 - 0.8	medium
0.8 -	large

Hay una escala comúnmente usada para interpretar el tamaño de un efecto en términos de la D de Cohen, mostrada en la Tabla 10.1. Puede ser útil observar algunos efectos comúnmente entendidos para ayudar a comprender estas interpretaciones. Por ejemplo, el tamaño del efecto para las diferencias de altura por género en personas adultas (d = 2.05) es muy grande en referencia a nuestra tabla anterior. También podemos ver esto al observar las distribuciones de las alturas de hombres y mujeres en una muestra del conjunto de datos de NHANES. La figura 10.3 muestra que las dos distribuciones están bastante bien separadas, aunque todavía se superponen, lo que destaca el hecho de que incluso cuando hay un tamaño de efecto muy grande para la diferencia entre dos grupos, habrá individuos de cada grupo que son más como el otro grupo.

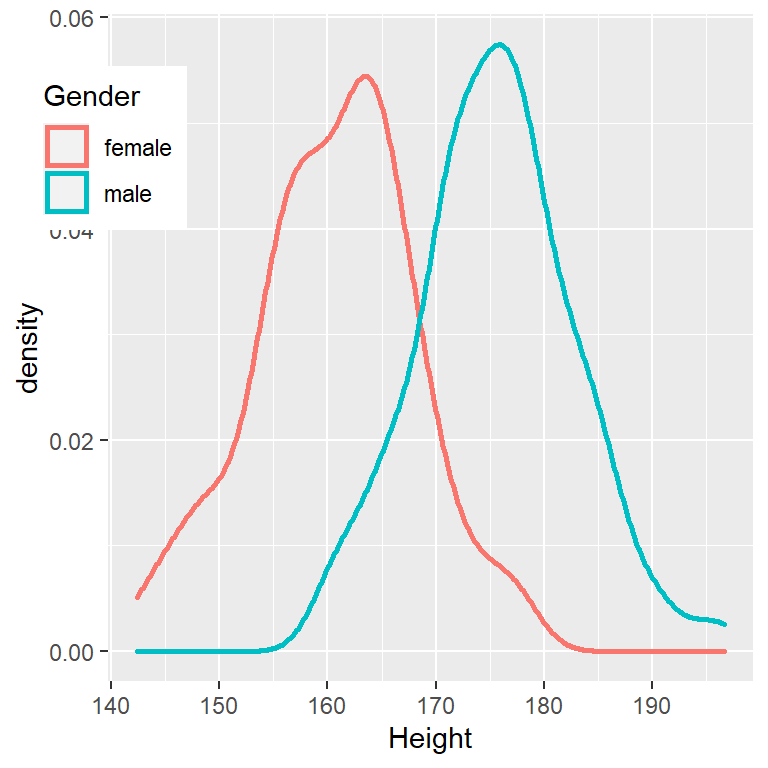
Figura 10.3: Gráficos de histograma suavizados para alturas masculinas y femeninas en el conjunto de datos de NHANES, que muestran distribuciones claramente distintas pero también claramente superpuestas.

También vale la pena señalar que rara vez encontramos efectos de esta magnitud en la ciencia, en parte porque son efectos tan obvios que no necesitamos investigación científica para encontrarlos. Como veremos en el Capítulo 17 sobre la reproducibilidad, los efectos muy grandes reportados en la investigación científica a menudo reflejan el uso de prácticas de investigación cuestionables en lugar de efectos verdaderamente enormes en la naturaleza. También vale la pena señalar que incluso para un efecto tan grande, las dos distribuciones aún se superponen: habrá algunas mujeres que serán más altas que el hombre promedio, y viceversa. Para la mayoría de los efectos científicos más interesantes, el grado de superposición será mucho mayor, por lo que no deberíamos sacar conclusiones sólidas de inmediato sobre personas de diferentes poblaciones basadas incluso en un tamaño de efecto grande.

10.2.2 r de Pearson

La r de Pearson, también conocida como el coeficiente de correlación, es una medida sobre la fuerza de la relación linear entre dos variables continuas. Hablaremos sobre correlación con mayor detalle en el capítulo 13, para que podamos guardar los detalles para ese capítulo aquí simplemente presentaremos r como una manera de cuantificar la relación entre dos variables.

r es una medida que varía de -1 a 1, donde el valor de 1 representa una perfecta relación positiva entre variables, 0 representa no relación y -1 representa una relación perfectamente negativa. La figura 10.4 muestra ejemplos de varios niveles de correlación utilizando datos generados aleatoriamente.

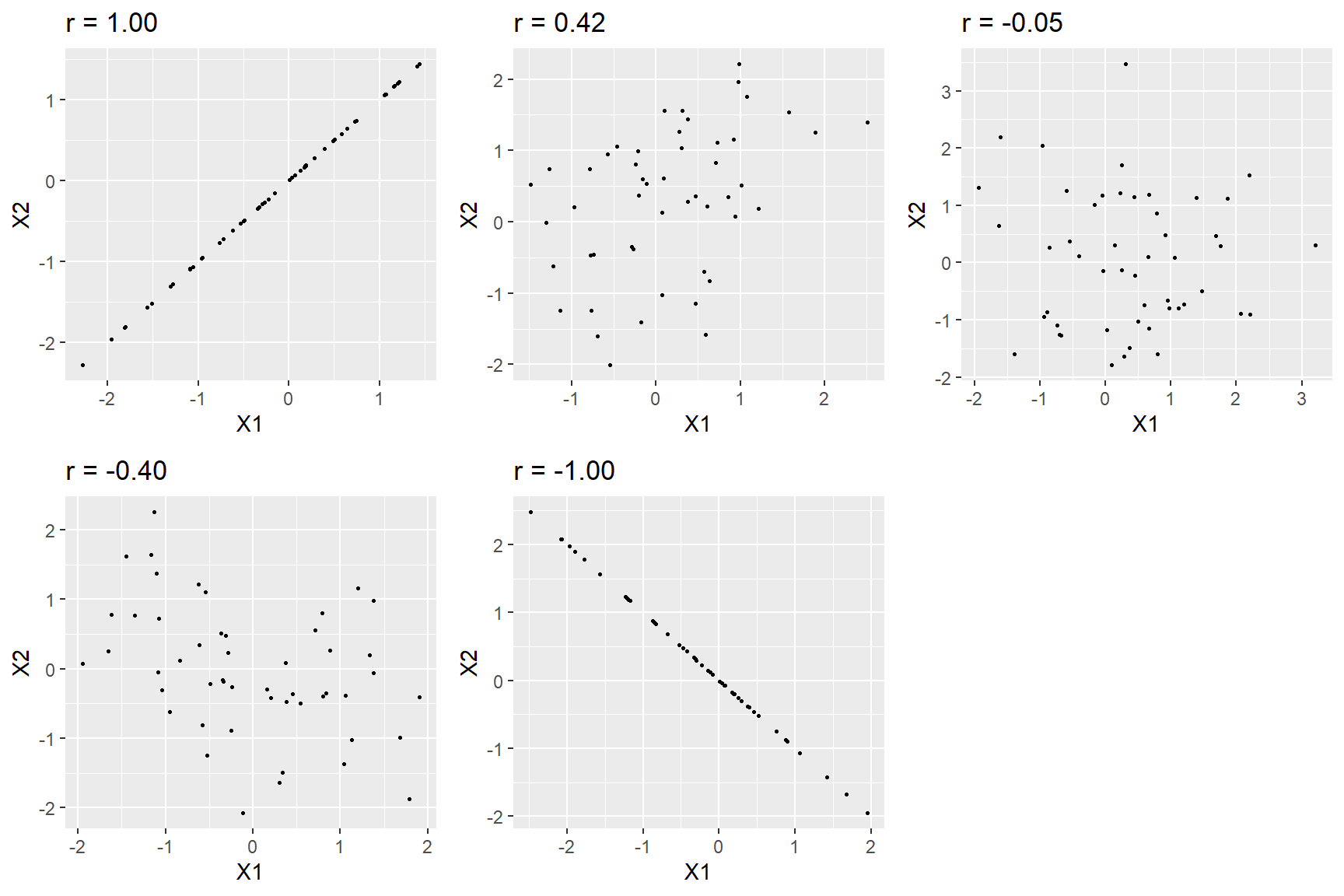
Figura 10.4: Ejemplos de varios niveles de la r de Pearson.

10.2.3 Razón de posibilidades (odds ratio)

En nuestra discusión anterior sobre probabilidad discutimos el concepto de las posibilidades – esto es, la probabilidad de que un evento suceda versus a que no suceda.

\[ odds\ of\ A = \frac{P(A)}{P(\neg A)} \]

También discutimos la razón de posibilidades (odds ratio) que es simplemente la razón entre dos posibilidades. La razón de posibilidades es una manera útil para describir tamaños de efectos para variables binarias.

Por ejemplo, tomemos el caso de fumar y el cáncer de pulmón. Un estudio publicado en el International Journal of Cancer en 2012 (Pesch et al. 2012) combinó datos sobre la aparición de cáncer de pulmón en fumadores y personas que nunca han fumado en una serie de estudios diferentes. Ten en cuenta que estos datos provienen de estudios de casos y controles, lo que significa que los participantes en los estudios fueron reclutados porque tenían o no tenían cáncer; luego se examinó su condición de fumador. Por tanto, estas cifras (mostradas en la Tabla 10.2) no representan la prevalencia del cáncer entre los fumadores de la población general, pero pueden informarnos sobre la relación entre el cáncer y el tabaquismo.

Tabla 10.2: Aparición del cáncer de pulmón por separado para los fumadores actuales y los que nunca han fumado.

Status	NeverSmoked	CurrentSmoker
No Cancer	2883	3829
Cancer	220	6784

Podemos convertir estos números en razones de posibilidades (odds ratios) para cada uno de los grupos. Las posibilidades de que un no fumador tenga cáncer de pulmón son 0.08 mientras que las posibilidades de que un fumador actual tenga cáncer de pulmón son 1.77. La razón de estas posibilidades nos dice acerca de la probabilidad relativa de cáncer entre los dos grupos: La razón de posibilidades de 23.22 nos dice que las posibilidades de cáncer de pulmón en los fumadores son aproximadamente 23 veces más altas que en los que nunca han fumado.

10.3 Poder estadístico

Recuerda del capítulo anterior que bajo el enfoque de prueba de hipótesis de Neyman-Pearson, tenemos que especificar nuestro nivel de tolerancia para dos tipos de errores: falsos positivos (que llamaron error tipo I) y falsos negativos (que llamaron error tipo II). La gente a menudo se enfoca mucho en el error de Tipo I, porque hacer una afirmación de falso positivo generalmente se ve como algo muy malo; por ejemplo, las afirmaciones ahora desacreditadas de Wakefield (1999) de que el autismo estaba asociado con la vacunación llevaron a un sentimiento antivacunas que ha resultado en un aumento sustancial de enfermedades infantiles como el sarampión. De manera similar, no queremos afirmar que un medicamento cura una enfermedad si realmente no lo hace. Es por eso que la tolerancia para los errores de Tipo I generalmente se establece bastante baja, generalmente en \(\alpha = 0.05\). Pero, ¿qué pasa con los errores de tipo II?

El concepto de poder estadístico (statistical power) es el complemento al tipo de error II – que es la probabilidad (likelihood) de encontrar un resultado positivo, dado que exista ese efecto:

\[ power = 1 - \beta \]

Otro aspecto importante del modelo de Neyman-Pearson que no discutimos anteriormente es el hecho de que además de especificar los niveles aceptables de errores de Tipo I y Tipo II, también tenemos que describir una hipótesis alternativa específica, es decir, ¿cuál es el tamaño del efecto que deseamos detectar? De lo contrario, no podemos interpretar \(\beta\); la probabilidad de encontrar un efecto grande siempre será mayor que encontrar un efecto pequeño, por lo que \(\beta\) será diferente dependiendo del tamaño del efecto que estemos tratando de detectar.

Existen tres factores que pueden afectar el poder estadístico:

• Tamaño de la muestra: las muestras más grandes proporcionan una mayor potencia estadística.
• Tamaño del efecto: cualquier diseño dado siempre tendrá mayor poder para encontrar un efecto grande que un efecto pequeño (porque encontrar efectos grandes es más fácil).
• Tasa de error tipo I: existe una relación entre el error de tipo I y la potencia de modo que (en igualdad de condiciones) la disminución del error de tipo I también disminuirá la potencia.

Podemos ver esto a través de la simulación. Primero simulemos un solo experimento, en el que comparamos las medias de dos grupos usando una prueba t estándar. Variaremos el tamaño del efecto (especificado en términos de la d de Cohen), la tasa de error de Tipo I y el tamaño de la muestra, y para cada uno de ellos examinaremos cómo se ve afectada la proporción de resultados significativos (es decir, el poder). La figura 10.5 muestra un ejemplo de cómo cambia la potencia en función de estos factores.

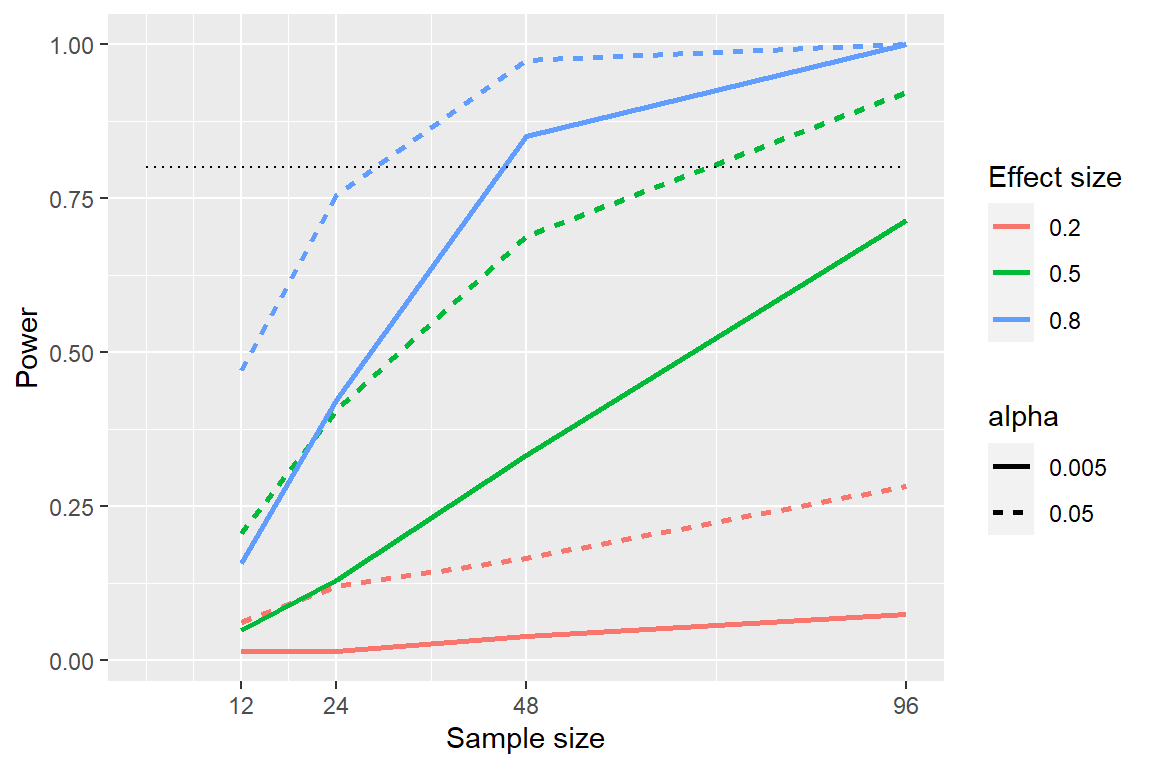
Figura 10.5: Resultados de la simulación de potencia, que muestran la potencia en función del tamaño de la muestra, con tamaños de efecto mostrados como diferentes colores y alfa como el tipo de línea. El criterio estándar del 80 por ciento de potencia se muestra mediante la línea negra punteada.

Esta simulación nos muestra que incluso con una muestra de 96, relativamente tendremos poco poder para encontrar un efecto pequeño (\(d = 0.2\)) con \(\alpha = 0.005\). Esto significa que un estudio diseñado para hacer esto sería fútil, o sea que está casi garantizado que no encontrará nada, incluso si un efecto real de ese tamaño existe.

Hay al menos dos razones importantes para preocuparse por el poder estadístico. Primero, si usted es unx investigadorx, probablemente no quiera perder su tiempo haciendo experimentos fútiles. Realizar un estudio con poca potencia es esencialmente fútil, porque significa que hay una probabilidad muy baja de que uno encuentre un efecto, incluso si existe. En segundo lugar, resulta que cualquier hallazgo positivo que provenga de un estudio con poca potencia es más probable que sea falso en comparación con un estudio con buena potencia, un punto que discutimos con más detalle en el Capítulo 17.

10.3.1 Análisis de poder

Afortunadamente, existen herramientas disponibles que nos permiten determinar el poder estadístico de un experimento. El uso más común de estas herramientas es en la planificación de un experimento, cuando nos gustaría determinar qué tan grande debe ser nuestra muestra para tener suficiente poder para encontrar nuestro efecto de interés.

Digamos que estamos interesadxs en realizar un estudio de cómo un rasgo de personalidad en particular difiere entre los usuarios de dispositivos iOS y Android. Nuestro plan es recolectar dos grupos de individuos y medirlos en función del rasgo de personalidad, y luego comparar los dos grupos usando una prueba t. En este caso, pensaríamos que un efecto mediano (\(d = 0.5\)) es de interés científico, por lo que usaremos ese nivel para nuestro análisis de poder. Para determinar el tamaño de muestra necesario, podemos utilizar la función de potencia/poder de nuestro software estadístico:

## 
##      Two-sample t test power calculation 
## 
##               n = 64
##           delta = 0.5
##              sd = 1
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Esto nos dice que necesitaríamos al menos 64 sujetos en cada grupo para tener suficiente poder para encontrar un efecto de tamaño medio. Siempre es importante realizar un análisis de poder antes de comenzar un nuevo estudio, para asegurarse de que el estudio no sea fútil debido a una muestra demasiado pequeña.

Puede que se le haya ocurrido que si el tamaño del efecto es lo suficientemente grande, la muestra necesaria será muy pequeña. Por ejemplo, si realizamos el mismo análisis de potencia con un tamaño del efecto de d=2, veremos que solo necesitamos unos 5 sujetos en cada grupo para tener la potencia suficiente para encontrar la diferencia.

## 
##      Two-sample t test power calculation 
## 
##               n = 5.1
##               d = 2
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Sin embargo, es raro en la ciencia estar haciendo un experimento en el que esperamos encontrar un efecto tan grande, al igual que no necesitamos estadísticas para decirnos que los niños de 16 años son más altos que los de 6 años. Cuando ejecutamos un análisis de poder, necesitamos especificar un tamaño de efecto que sea plausible y/o científicamente interesante para nuestro estudio, que normalmente provendría de investigaciones previas. Sin embargo, en el Capítulo 17 discutiremos un fenómeno conocido como la “maldición del ganador” que probablemente resulte en tamaños de efecto publicados mayores que el tamaño del efecto real, por lo que esto también debe tenerse en cuenta.

10.4 Objetivos de aprendizaje

Después de leer este capítulo, deberías poder:

• Describir la interpretación adecuada de un intervalo de confianza y calcular un intervalo de confianza para la media de un conjunto de datos dado.
• Definir el concepto de tamaño del efecto y calcular el tamaño del efecto para una prueba determinada.
• Describir el concepto de poder estadístico y por qué es importante para la investigación.

10.5 Lecturas sugeridas

• Robust misinterpretation of confidence intervals, por Hoekstra et al.

Referencias

Neyman, J. 1937. “Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 236 (767): 333–80. https://doi.org/10.1098/rsta.1937.0005.

Pesch, Beate, Benjamin Kendzia, Per Gustavsson, Karl-Heinz Jöckel, Georg Johnen, Hermann Pohlabeln, Ann Olsson, et al. 2012. “Cigarette Smoking and Lung Cancer–Relative Risk Estimates for the Major Histological Types from a Pooled Analysis of Case-Control Studies.” Int J Cancer 131 (5): 1210–19. https://doi.org/10.1002/ijc.27339.

Schenker, Nathaniel, and Jane F. Gentleman. 2001. “On Judging the Significance of Differences by Examining the Overlap Between Confidence Intervals.” The American Statistician 55 (3): 182–86. http://www.jstor.org/stable/2685796.

Sullivan, Gail M, and Richard Feinn. 2012. “Using Effect Size-or Why the p Value Is Not Enough.” J Grad Med Educ 4 (3): 279–82. https://doi.org/10.4300/JGME-D-12-00156.1.

Wakefield, A J. 1999. “MMR Vaccination and Autism.” Lancet 354 (9182): 949–50. https://doi.org/10.1016/S0140-6736(05)75696-8.