Capitulo 13 Modelar relaciones continuas

La mayoría de las personas están familiarizadas con el concepto de correlación, no obstante en este capíttulo proveeremos un entendimiento más formal para este concepto comúnmente usado y malentendido.

13.1 Un ejemplo: Crímenes de odio y desigualdad de ingreso

En 2017, el sitio web Fivethirtyeight.com publicó una historia titulada Higher Rates Of Hate Crimes Are Tied To Income Inequality en la cual se discute la relación entre la prevalencia de los crímenes de odio y la desigualdad de ingreso al inicio de la elección presidencial de 2016. La historia reportó un análisis de datos del FBI acerca de crímenes de odio y del Centro de leyes Southern Poverty, basados en esto informan:

“Descubrimos que la desigualdad de ingresos era el determinante más significativo de los delitos de odio e incidentes de odio ajustados a la población en los Estados Unidos.”

Los datos de este análisis están disponibles como parte del fivethirtyeight, un paquete para el software estadístico de R, el cual facilita nuestro acceso a él. El análisis reportado en la historia se focaliza en la relación entre la desigualdad de ingresos (definida por una medida llamada índice Gini — véase Apéndice para más detalles) y la prevalencia de crímenes de odio de cada estado.

13.2 ¿La desigualdad de ingreso está relacionada con los crímenes de odio?

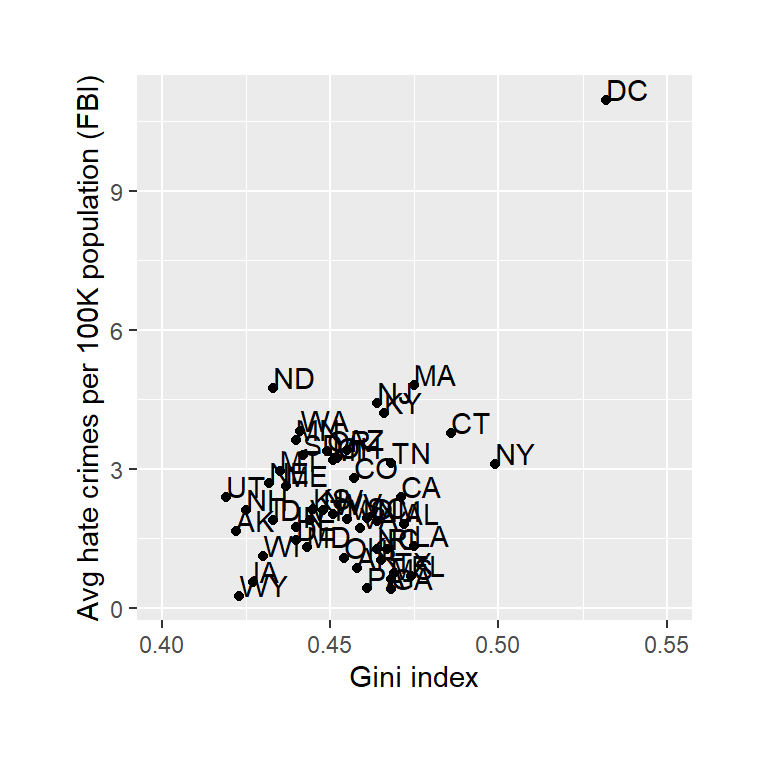
Figura 13.1: Gráfica de tasas de crímenes de odio vs. Índice Gini.

La relación entre la inequidad de ingreso y los índices de crímenes de odio se muestra en la Figura 13.1. Observando los datos, parece que puede haber una relación positiva entre ambas variables. ¿Cómo podemos cuantificar esa relación?

13.3 Covarianza y correlación

Una manera de cuantificar la relación entre dos variables es la covarianza. Recuerda que la varianza para una sola variable se calcula como el promedio de las diferencias cuadráticas entre cada punto de los datos y la media:

\[ s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{N - 1} \]

Esto nos indica qué tan lejana está cada observación de la media, en promedio, en unidades cuadradas. La covarianza nos indica si hay una relación entre las desviaciones de dos variables diferentes a lo largo de las observaciones. Esto se define como:

\[ covariance = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{N - 1} \]

Este valor estará lejos de cero cuando los puntos individuales de los datos se desvíen en cantidades similares de sus respectivas medias; si se desvían en la misma dirección, la covarianza es positiva, mientras que si se desvían en direcciones opuestas, la covarianza es negativa. Veamos primero un ejemplo de juguete. Los datos se muestran en la Tabla 13.1, junto con sus desviaciones individuales de la media y sus productos cruzados (crossproducts).

Tabla 13.1: Datos del ejemplo de juguete para covarianzas.

x	y	y_dev	x_dev	crossproduct
3	5	-3.6	-4.6	16.56
5	4	-4.6	-2.6	11.96
8	7	-1.6	0.4	-0.64
10	10	1.4	2.4	3.36
12	17	8.4	4.4	36.96

La covarianza es simplemente la media de los productos cruzados (crossproducts), en este caso es 17.05. Por lo general, no usamos la covarianza para describir relaciones entre variables, porque varía con el nivel general de varianza en los datos. En su lugar, usualmente usamos el coeficiente de correlación (a menudo referido como correlación de Pearson en honor al estadístico Karl Pearson). La correlación se calcula escalando la covarianza sobre las desviaciones estándar de las dos variables:

\[ r = \frac{covariance}{s_xs_y} = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{(N - 1)s_x s_y} \] En este caso , el valor es 0.89. El coeficiente de correlación es útil porque varía entre -1 y 1 independientemente de la naturaleza de los datos; de hecho, ya discutimos el coeficiente de correlación anteriormente en nuestra discusión de los tamaños del efecto. Como vimos en ese capítulo anterior, una correlación de 1 indica una relación lineal perfecta, una correlación de -1 indica una relación negativa perfecta y una correlación de cero indica que no hay relación lineal.

13.3.1 Prueba de hipótesis para correlaciones

El valor de correlación de 0.42 entre crímenes de odio y la desigualdad de ingreso parece indicar una relación razonablemente fuerte entre los dos, pero también podemos imaginar que esto puede suceder al azar incluso si no hay relación. Podemos probar la hipótesis nula de que la correlación es cero, utilizando una simple ecuación que nos permita convertir el valor de correlación en un estadístico t: \[ \textit{t}_r = \frac{r\sqrt{N-2}}{\sqrt{1-r^2}} \]

Bajo la hipótesis nula \(H_0:r=0\), este estadístico se distribuye como una distribución t con \(N - 2\) grados de libertad. Podemos calcular esto utilizando nuestro software estadístico:

## 
##  Pearson's product-moment correlation
## 
## data:  hateCrimes$avg_hatecrimes_per_100k_fbi and hateCrimes$gini_index
## t = 3, df = 48, p-value = 0.002
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.16 0.63
## sample estimates:
##  cor 
## 0.42

Esta prueba nos muestra que la probabilidad de un valor r así o más extremo es realmente baja bajo la hipótesis nula, así que rechazaríamos la hipótesis nula de \(r=0\). Nota que este test asume que ambas variables están normalmente distribuidas.

También podríamos probar esto por aleatorización, en la que mezclamos (reordenamos) los valores de una de las variables y calculamos la correlación, repetidamente, luego comparamos el valor observado de nuestra correlación con esta distribución nula para determinar qué tan probable sería nuestro valor observado bajo la hipótesis nula. Los resultados se muestran en la Figura 13.2. El valor p calculado usando la aleatorización es razonablemente similar a la respuesta dada por la prueba t.

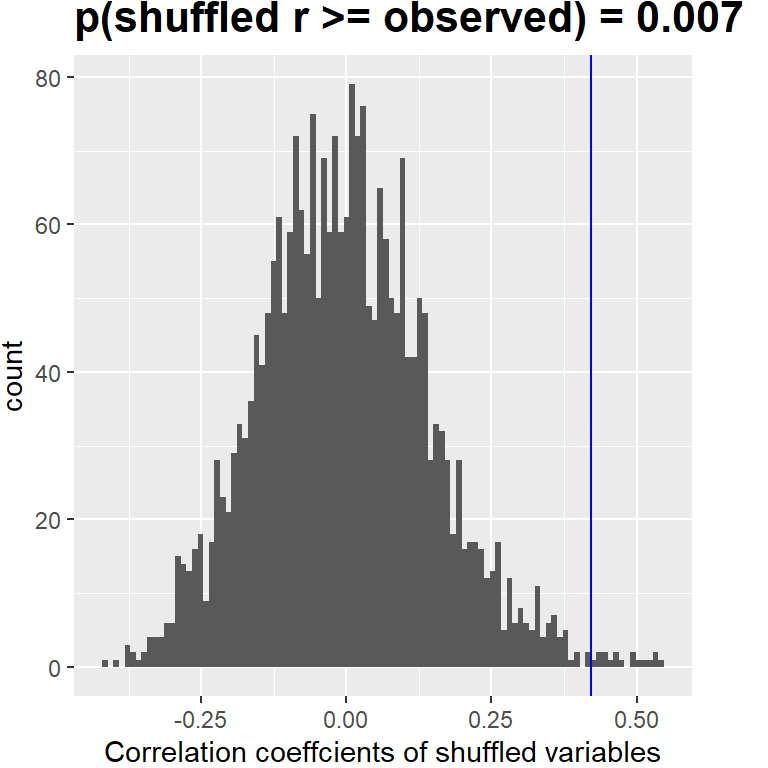
Figura 13.2: Histograma de los valores de correlación bajo la hipótesis nula, obtenidos al mezclar los valores. El valor observado está marcado por la línea azul.

También podríamos usar inferencia Bayesiana para estimar la correlación; véase el Apéndice para más sobre esto.

13.3.2 Correlaciones robustas

Podrás haber notado algo un poco extraño en la Figura 13.1 – uno de los puntos de los datos (el del Distrito de Columbia) parece estar un tanto separado de los otros. Nos referimos a esto como un valor atípico o outlier, y el coeficiente de correlación estándar es muy sensible a valores atípicos. Por ejemplo, en la figura 13.3 podemos ver cómo un solo punto de datos periférico puede causar un valor de correlación positivo muy alto, incluso cuando la relación real entre los otros puntos de datos es perfectamente negativa.

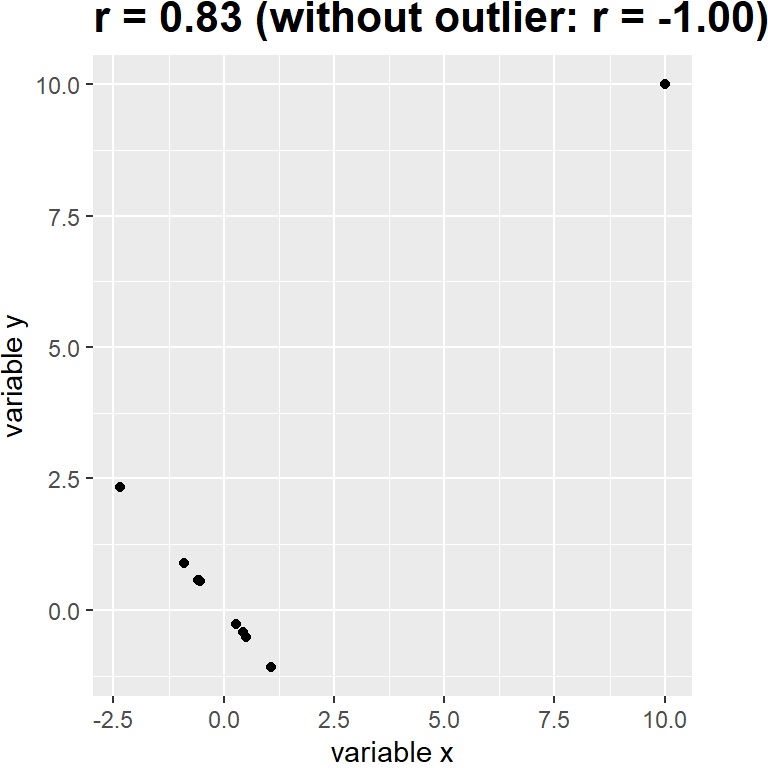
Figura 13.3: Un ejemplo simulado de los efectos de los valores atípicos o outliers sobre la correlación. Sin el outlier, el resto de los datos tienen una correlación negativa perfecta, pero ese solo valor atípico cambia el valor de la correlación a uno positivo alto.

Una manera de abordar los valores atípicos es calcular la correlación sobre los rangos (ranks) de los datos después de ordenarlos, en lugar de sobre los datos mismos; esto es conocido como la correlación de Spearman. Mientras que la correlación de Pearson en el ejemplo de la Figura 13.3 era 0.83, la correlación de Spearman es -0.45 mostrando que la correlación de rangos (rank correlation) reduce el efecto del valor atípico y refleja la relación negativa entre la mayoría de los puntos de datos.

Podemos calcular la correlación de rangos de los datos de crímenes de odio también:

## 
##  Spearman's rank correlation rho
## 
## data:  hateCrimes$avg_hatecrimes_per_100k_fbi and hateCrimes$gini_index
## S = 20146, p-value = 0.8
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##   rho 
## 0.033

Ahora podemos ver que la correlación ya no es significativa (y en efecto es muy cercana a cero), sugiriendo que las afirmaciones del blog FiveThirtyEight pueden haber sido incorrectas debido al efecto del valor atípico.

13.4 Correlación y causalidad

Cuando decimos que una cosa causa otra, ¿a qué nos referimos? Hay una larga historia en filosofía de la discusión acerca del significado de la causalidad, pero en estadística una manera más común de pensar en la causalidad es en términos de control experimental. Eso es, si pensamos que el factor X causa el factor Y, entonces si manipulamos el valor de X afectará el valor de Y.

En medicina, hay un conjunto de ideas conocidas como los postulados de Koch (Koch’s postulates) que históricamente se han utilizado para determinar si un organismo en particular causa una enfermedad. La idea básica es que el organismo debe estar presente en las personas con la enfermedad y no en las que no la padecen; por lo tanto, un tratamiento que elimine el organismo también debe eliminar la enfermedad. Además, infectar a alguien con el organismo debería hacer que contraiga la enfermedad. Un ejemplo de esto se vio en el trabajo del Dr. Barry Marshall, quien tenía la hipótesis de que las úlceras de estómago eran causadas por una bacteria (Helicobacter pylori). Para demostrar esto, se infectó con la bacteria y poco después desarrolló una inflamación severa en su estómago. Luego se trató a sí mismo con un antibiótico y su estómago pronto se recuperó. Más tarde ganó el Premio Nobel de Medicina por este trabajo.

A menudo nos gustaría probar hipótesis causales, pero en realidad no podemos hacer un experimento, ya sea porque es imposible (“¿Cuál es la relación entre las emisiones de carbono humano y el clima de la Tierra?”) o porque no es ético (“¿Cuáles son los efectos del abuso severo sobre el desarrollo del cerebro infantil?”). Sin embargo, aún podemos recopilar datos que podrían ser relevantes para esas preguntas. Por ejemplo, potencialmente podemos recopilar datos de niños que han sido abusados y de aquellos que no, y luego podemos preguntarnos si su desarrollo cerebral es diferente.

Digamos que hicimos tal análisis y encontramos que los niños abusados tenían un desarrollo cerebral más pobre que los niños no abusados. ¿Demostraría esto que el abuso causa un peor desarrollo cerebral? No. Siempre que observemos una asociación estadística entre dos variables, es ciertamente posible que una de esas dos variables cause la otra. Sin embargo, también es posible que ambas variables estén influenciadas por una tercera variable; en este ejemplo, podría ser que el abuso infantil esté asociado con el estrés familiar, que también podría causar un desarrollo cerebral más deficiente debido a una menor interacción intelectual, estrés alimentario o muchas otras posibles vías. El punto es que una correlación entre dos variables generalmente nos dice que algo probablemente está causando otra cosa, pero no nos dice qué está causando qué.

13.4.1 Gráficas causales

Una forma útil de describir las relaciones causales entre variables es mediante un gráfico causal (causal graph), que muestra las variables como círculos y las relaciones causales entre ellas como flechas. Por ejemplo, la Figura 13.4 muestra las relaciones causales entre el tiempo de estudio y dos variables que creemos que deberían verse afectadas por él: las calificaciones del examen y los tiempos de finalización del examen.

Sin embargo, en realidad, los efectos sobre el tiempo de finalización y las calificaciones no se deben directamente a la cantidad de tiempo dedicado al estudio, sino más bien a la cantidad de conocimientos que adquiere el alumno al estudiar. Por lo general, diríamos que el conocimiento es una variable latente, es decir, no podemos medirlo directamente, pero podemos verlo reflejado en variables que podemos medir (como calificaciones y tiempos de finalización). La Figura 13.5 muestra esto.

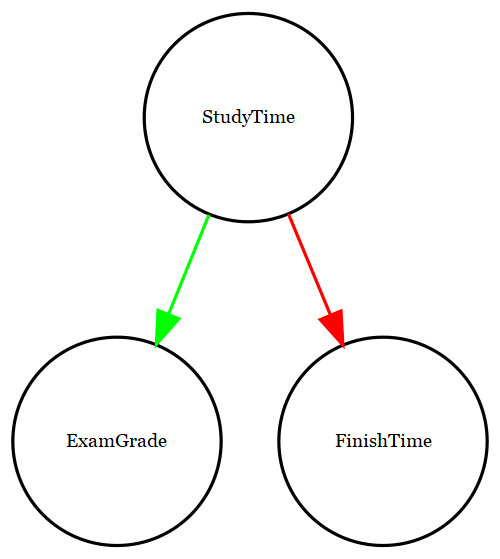
Figura 13.4: Una gráfica mostrando las relaciones causales entre tres variables: tiempo de estudio, calificaciones de exámenes, y tiempos de finalización de exámenes. Una flecha verde representa una relación positiva (esto es, más tiempo de estudio causa mayor calificación en exámenes), y una flecha roja representa una relación negativa (esto es, más tiempo de estudio causa menor tiempo para finalizar un examen).

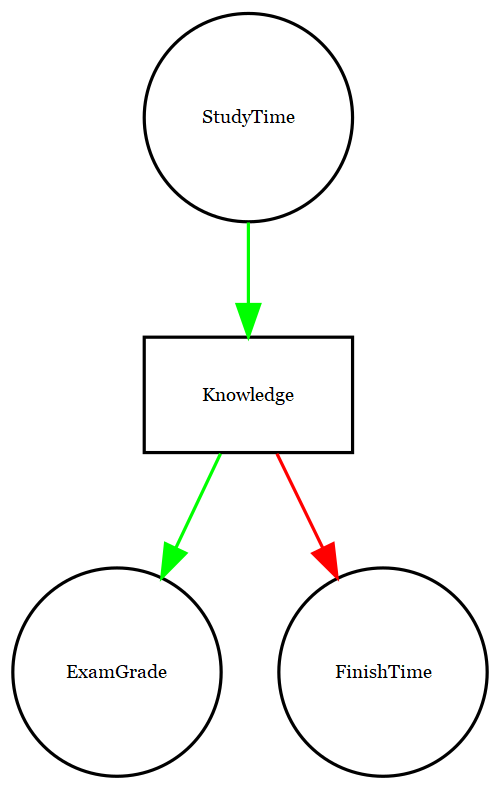
Figura 13.5: Una gráfica mostrando las mismas relaciones causales que antes, pero ahora también mostrando la variable latente (conocimiento) en un cuadro.

Aquí diríamos que el conocimiento media la relación entre el tiempo de estudio y las calificaciones/tiempos de finalización. Eso significa que si pudiéramos mantener el conocimiento constante (por ejemplo, administrando un medicamento que causa el olvido inmediato), entonces la cantidad de tiempo de estudio ya no debería tener un efecto sobre las calificaciones y los tiempos de finalización.

Nota que si simplemente midiéramos las calificaciones de los exámenes y los tiempos de finalización, generalmente veríamos una relación negativa entre ellos, porque las personas que terminan los exámenes más rápido obtienen las calificaciones más altas. Sin embargo, si interpretáramos esta correlación como una relación causal, esto nos diría que para obtener mejores calificaciones, ¡deberíamos terminar el examen más rápido! Este ejemplo muestra lo engañosa que puede ser la inferencia de causalidad a partir de datos no experimentales.

En las áreas de la estadística y del aprendizaje automático (machine learning), existe una comunidad de investigación muy activa que actualmente está estudiando la cuestión de cuándo y cómo podemos inferir relaciones causales a partir de datos no experimentales. Sin embargo, estos métodos a menudo requieren suposiciones fuertes y, en general, deben usarse con gran precaución.

13.5 Objetivos de aprendizaje

Después de leer este capítulo tú deberás ser capaz de:

• Describir el concepto del coeficiente de correlación y su interpretación.
• Calcular la correlación entre dos variables continuas.
• Describir las posibles influencias causales que pueden dar lugar a una correlación observada.

13.6 Lecturas sugeridas

• The Book of Why por Judea Pearl - una excelente introducción a las ideas detrás de la inferencia causal.

13.7 Apéndice:

13.7.1 Cuantificando la desigualdad: El índice Gini

Antes de que miremos el análisis reportado en la historia, primero es útil entender cómo se usa el índice de Gini para cuantificar la desigualdad. El índice de Gini generalmente se define en términos de una curva que describe la relación entre los ingresos y la proporción de la población que tiene ingresos en ese nivel o menos, conocida como curva de Lorenz. Sin embargo, otra forma de pensarlo es más intuitiva: es la diferencia absoluta media relativa (relative mean absolute difference) entre ingresos, dividida entre dos (de https://en.wikipedia.org/wiki/Gini_coefficient):

\[ G = \frac{\displaystyle{\sum_{i=1}^n \sum_{j=1}^n \left| x_i - x_j \right|}}{\displaystyle{2n\sum_{i=1}^n x_i}} \]

<!.. fig.cap=“Lorenz curves for A) perfect equality, B) normally distributed income, and C) high inequality (equal income except for one very wealthy individual).” –>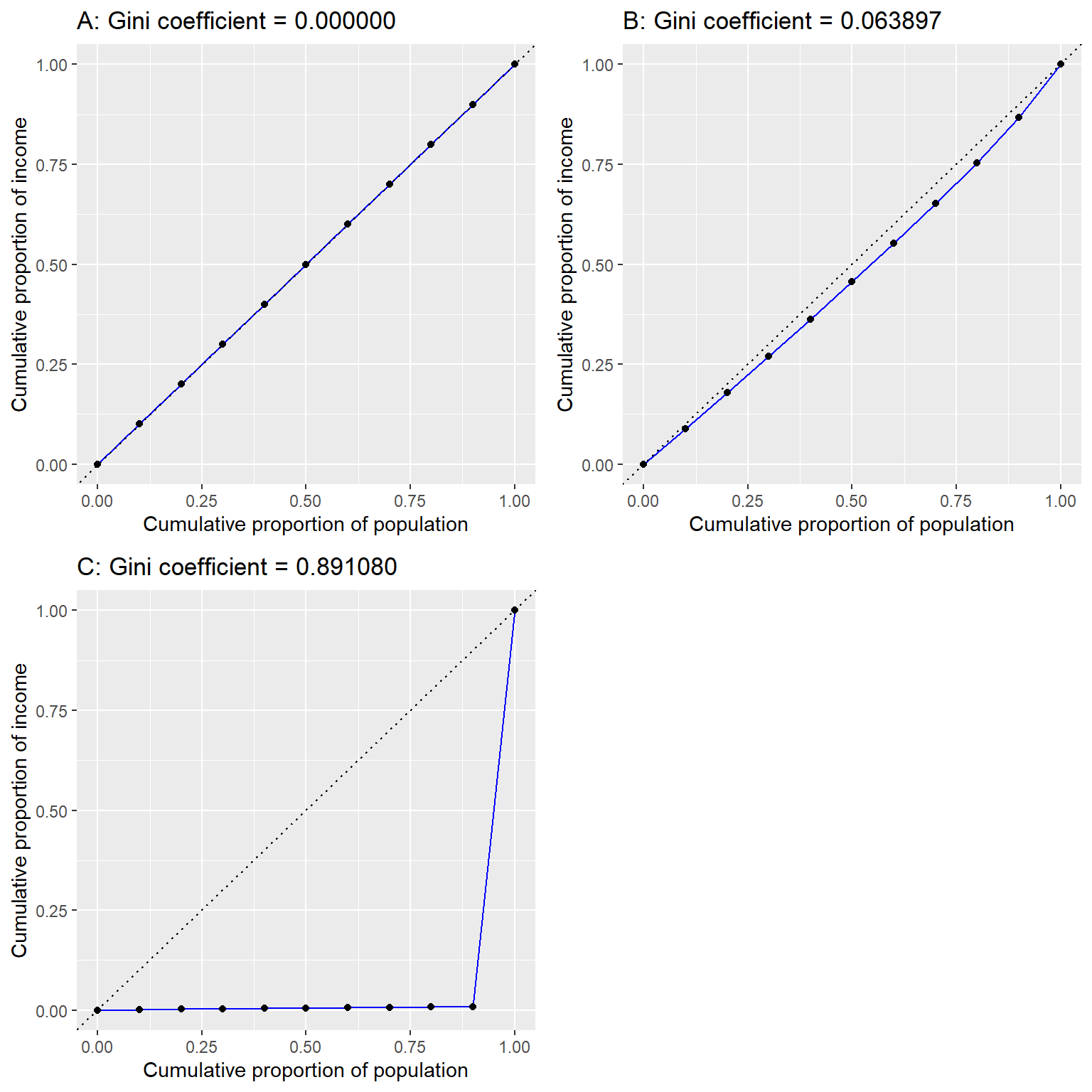

Figura 13.6: Curvas de Lorenz para A) igualdad perfecta, B) ingreso distribuido normalmente, y C) alta desigualdad (ingreso igual a excepción de una sola persona con muy altos ingresos).

La Figura 13.6 muestra las curvas de Lorenz para varias distribuciones de ingresos diferentes. El panel superior izquierdo (A) muestra un ejemplo con 10 personas donde todos tienen exactamente los mismos ingresos. La longitud de los intervalos entre puntos es igual, lo que indica que cada persona gana una parte idéntica del ingreso total de la población. El panel superior derecho (B) muestra un ejemplo donde los ingresos se distribuyen normalmente. El panel inferior izquierdo muestra un ejemplo con alta desigualdad; todos tienen los mismos ingresos ($40,000) excepto una persona, que tiene ingresos de $40,000,000. Según el censo de EE.UU., Estados Unidos tenía un índice de Gini de 0,469 en 2010, aproximadamente a la mitad entre nuestros ejemplos de distribución normal y máxima desigualdad.

13.7.2 Análisis de correlación bayesiana

También podemos analizar los datos de FiveThirtyEight utilizando el análisis bayesiano, que tiene dos ventajas. Primero, nos proporciona una probabilidad posterior, en este caso, la probabilidad de que el valor de correlación sea superior a cero. En segundo lugar, la estimación bayesiana combina la evidencia observada con una probabilidad previa, que tiene el efecto de regularizar la correlación estimada, efectivamente llevándola hacia cero. Aquí podemos calcularlo usando el paquete BayesFactor en R.

## Bayes factor analysis
## --------------
## [1] Alt., r=0.333 : 21 ±0%
## 
## Against denominator:
##   Null, rho = 0 
## ---
## Bayes factor type: BFcorrelation, Jeffreys-beta*

## Summary of Posterior Distribution
## 
## Parameter | Median |       95% CI |     pd |          ROPE | % in ROPE |    BF |         Prior
## ----------------------------------------------------------------------------------------------
## rho       |   0.38 | [0.16, 0.60] | 99.88% | [-0.05, 0.05] |        0% | 20.85 | Beta (3 +- 3)

Nótese que la correlación estimada usando el método bayesiano (0.38) es ligeramente menor que la estimada usando el coeficiente de correlación estándar (0.42), lo cual se debe al hecho de que la estimación se basa en una combinación de la evidencia y de la probabilidad previa, lo que efectivamente reduce la estimación hacia cero. Sin embargo, observe que el análisis bayesiano no es robusto para el valor atípico, y todavía dice que hay evidencia bastante fuerte de que la correlación es mayor que cero (con un factor de Bayes mayor a 20).