Capitulo 7 Muestreo
Una de las ideas fundamentales en estadística es que podemos hacer inferencias acerca de una población completa basadas en una muestra relativamente pequeña de individuos de esa población. En este capítulo vamos a introducir el concepto estadístico de muestreo (sampling) y discutiremos cómo funciona.
Cualquiera viviendo en Estados Unidos está familiarizadx con el concepto de muestreo de las encuestas políticas que se han convertido en un tema central de nuestro proceso electoral. En algunos casos, estas encuestas pueden ser increíblemente acertadas al predecir los resultados de las elecciones. El mejor ejemplo proviene de las elecciones presidenciales de 2008 y 2012, cuando el encuestador Nate Silver predijo correctamente los resultados de 49 de 50 estados en 2008 y todos los 50 estados en 2012. Silver hizo esto mediante la combinación de 21 diferentes encuestas, las cuales varían en el grado en que tienden a inclinarse ya sea al lado republicano o demócrata. Cada una de estas encuestas incluye datos de 1000 votantes – lo que significa que Silver fue capaz de casi predecir perfectamente el patrón de los votos de más de 125 millones de votantes utilizando datos de aproximadamente 21,000 personas, junto con otros conocimientos (tales como la forma en la que estos estados han votado en el pasado).
7.1 ¿Cómo hacemos una muestra?
Nuestro objetivo en el muestreo es determinar el valor de una estadística para una populación entera de interés, utilizando únicamente un subconjunto de dicha población. Hacemos esto primeramente para ahorrar tiempo y esfuerzo – ¿por qué iríamos tras la batalla de medir cada individuo en la población si con una pequeña muestra es más que suficiente para estimar precisamente la estadística de interés?
En el ejemplo de las elecciones, la población son todos los votantes registrados en la región siendo encuestada, y la muestra es el conjunto de los 1000 individuos seleccionados por la organización encuestada. La manera en la que seleccionamos la muestra es crítica para asegurar que la muestra es representativa de la población entera, el cual es el objetivo principal del muestreo estadístico. Es fácil imaginar una muestra no representativa; si unx encuestadorx únicamente llama a personas cuyos nombres haya recibido del partido demócrata, entonces sería poco probable que los resultados de la encuesta fueran representativos de una población completa. En general, definiríamos una encuesta representativa como una en la que cada miembro de la población tiene la misma oportunidad de ser seleccionado. Cuando esto falla, tenemos entonces que preocuparnos acerca de si la estadística que calculamos está sesgada - esto es, si el valor es sistemáticamente diferente del valor poblacional (al que nos referimos como parámetro). Mantén en mente que generalmente no conocemos este parámetro poblacional, ¡porque si lo supiéramos no necesitaríamos hacer una muestra! Pero usaremos ejemplos donde tenemos acceso a una población entera, para poder explicar algunas ideas clave.
Es importante distinguir entre dos modos muy diferentes de muestreo: con reemplazo versus sin reemplazo. En el muestreo con reemplazo, después de que un miembro de la población ha sido muestreado, es puesto de regreso al grupo para que pueda ser potencialmente muestrado otra vez. En el muestreo sin reemplazo, una vez que lxs miembrxs han sido muestreadxs no son elegibles para ser muestredos otra vez. Es más común utilizar el muestreo sin reemplazo, pero hay algunos contextos en los cuales vamos a utilizar el muestreo con reemplazo, como cuando discutimos la técnica llamada bootstrapping en el capítulo 8.
7.2 Error de muestreo
Independientemente de qué tan representativa sea nuestra muestra, es muy probable que la estadística que calculemos de esa muestra vaya a diferir al menos ligeramente del parámetro poblacional. Nos referimos a esto como error de muestreo (sampling error). Si tomamos múltiples muestras, el valor de nuestro estimado estadístico va a variar de muestra a muestra; nos referimos a esta distribución de nuestra estadística a lo largo de diferentes muestras como distribución muestral.
El error de muestreo está directamente relacionado a la calidad de nuestra medición de la población. Claramente queremos que los estimados obtenidos de nuestra muestra sean lo más cercanos posible al verdadero valor del parámetro poblacional. Sin embargo, incluso cuando nuestra estadística no está sesgada (esto es, que esperamos que tenga el mismo valor que el parámetro poblacional), el valor para cualquier estimado particular va a diferir del valor poblacional, y esas diferencias van a ser mayores cuando el error de muestreo sea mayor. De este modo, reducir el error de muestreo es un paso importante para mejorar la medición.
Vamos a usar el conjunto de datos NHANES como ejemplo; vamos a asumir que el conjunto de datos NHANES es toda nuestra población de interés, y luego extraeremos muestras de datos aleatorios de dicha población. Mencionaremos más en el siguiente capítulo acerca de cómo funcionan las muestras “aleatorias” en un software estadístico.
En este ejemplo, sabemos que la media de la población adulta es (168.35) y la desviación estándar (10.16) para la altura porque estamos asumiendo que el conjunto de datos NHANES es la población. La Tabla 7.1 muestra estadísticos calculados de algunas muestras de 50 personas de la población NHANES.
| sampleMean | sampleSD |
|---|---|
| 167 | 9.1 |
| 171 | 8.3 |
| 170 | 10.6 |
| 166 | 9.5 |
| 168 | 9.5 |
La media y la desviación estándar de la muestra son similares pero no exactamente iguales a los valores de la población. Ahora tomemos una gran cantidad de muestras de 50 individuos, calculemos la media de cada muestra y observemos la distribución muestral de medias resultante. Tenemos que decidir cuántas muestras tomar para hacer un buen trabajo en la estimación de la distribución muestral – en este caso, tomaremos 5000 muestras para estar muy segurxs de la respuesta. Ten en cuenta que simulaciones como esta a veces pueden tardar unos minutos en ejecutarse y pueden hacer que tu computadora resople y reniege. El histograma de la Figura 7.1 muestra que las medias estimadas para cada una de las muestras de 50 individuos varían un poco, pero que en general se centran en la media de la población. El promedio de las 5000 medias muestrales (168.3463) está muy cerca de la media poblacional real (168.3497).
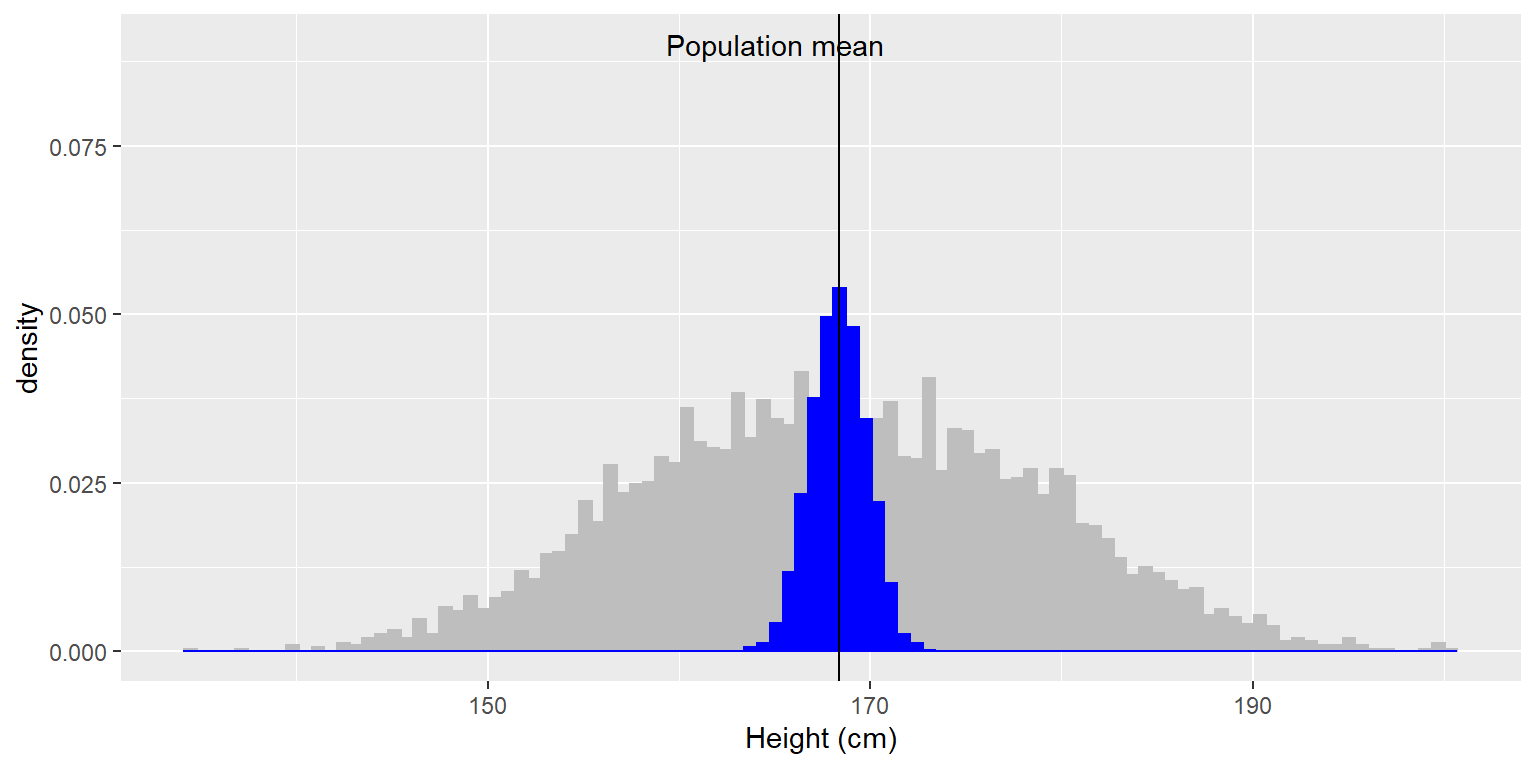
Figura 7.1: El histograma azul muestra la distribución muestral de la media de más de 5000 muestras aleatorias del conjunto de datos NHANES. El histograma del conjunto de datos completo se muestra en gris como referencia.
7.3 Error estándar de la media
Más adelante en el libro será esencial poder caracterizar qué tan variables son nuestras muestras, para poder hacer inferencias sobre la estadística de la muestra. Para la media, hacemos esto utilizando una cantidad llamada error estándar de la media (SEM, standard error of the mean), podemos pensar en ella como la desviación estándar de la distribución muestral de las medias. Para calcular el error estándar de la media para nuestra muestra, dividimos la desviación estándar estimada entre la raíz cuadrada del tamaño de la muestra:
\[ SEM = \frac{\hat{\sigma}}{\sqrt{n}} \]
Nota que tenemos que ser cuidadoses al calcular el error estándar de la media utilizando la desviación estándar estimada si nuestra muestra es pequeña (menor que 30).
Debido a que tenemos muchas muestras de la población NHANES y realmente conocemos el SEM de la población (que calculamos dividiendo la desviación estándar de la población entre el tamaño de la población), podemos confirmar que el SEM que se calculó usando el parámetro de población (1.44) está muy cerca de la desviación estándar observada de las medias para las muestras que tomamos del conjunto de datos NHANES (1.43).
La fórmula para el error estándar de la media implica que la calidad de nuestra medición involucra dos cantidades: la variabilidad de la población y el tamaño de nuestra muestra. Dado que el tamaño de la muestra es el denominador en la fórmula de SEM, un tamaño de muestra más grande producirá un SEM más pequeño cuando se mantiene constante la variabilidad de la población. No tenemos control sobre la variabilidad de la población, pero sí tenemos control sobre el tamaño de la muestra. Por lo tanto, si deseamos mejorar nuestras estadísticas muestrales (reduciendo su variabilidad muestral), entonces deberíamos utilizar muestras más grandes. Sin embargo, la fórmula también nos dice algo muy fundamental sobre el muestreo estadístico, a saber, que la utilidad de muestras más grandes disminuye con la raíz cuadrada del tamaño de la muestra. Esto significa que duplicar el tamaño de la muestra no duplicará la calidad de las estadísticas; más bien, lo mejorará en un factor de \(\sqrt{2}\). En la Sección 10.3 discutiremos la potencia estadística, que está íntimamente ligada a esta idea.
7.4 El teorema del límite central
El teorema del límite central nos dice que a medida que el tamaño de la muestra aumenta, la distribución muestral de la media se distribuirá normalmente, incluso si los datos dentro de cada muestra no se distribuyen normalmente.
Primero, comentemos un poco sobre la distribución normal. También se conoce como la distribución gaussiana, en honor a Carl Friedrich Gauss, un matemático que no la inventó pero que jugó un papel en su desarrollo. La distribución normal se describe en términos de dos parámetros: la media (que puede considerarse como la ubicación del pico) y la desviación estándar (que especifica el ancho de la distribución). La forma de campana de la distribución nunca cambia, solo su ubicación y ancho. La distribución normal se observa comúnmente en los datos recopilados en el mundo real, como ya hemos visto en el capítulo 3 – y el teorema del límite central nos da una idea de por qué ocurre eso.
Para ver el teorema del límite central en acción, trabajemos con la variable \(AlcoholYear\) del conjunto de datos NHANES, que está muy sesgada, como se muestra en el panel izquierdo de la Figura 7.2. Esta distribución es, a falta de una palabra mejor, original – y definitivamente no se distribuye normalmente. Ahora veamos la distribución muestral de la media de esta variable. La Figura 7.2 muestra la distribución muestral para esta variable, que se obtiene extrayendo repetidamente muestras de tamaño 50 del conjunto de datos NHANES y tomando la media. A pesar de la clara no normalidad de los datos originales, la distribución muestral es notablemente cercana a la normal.
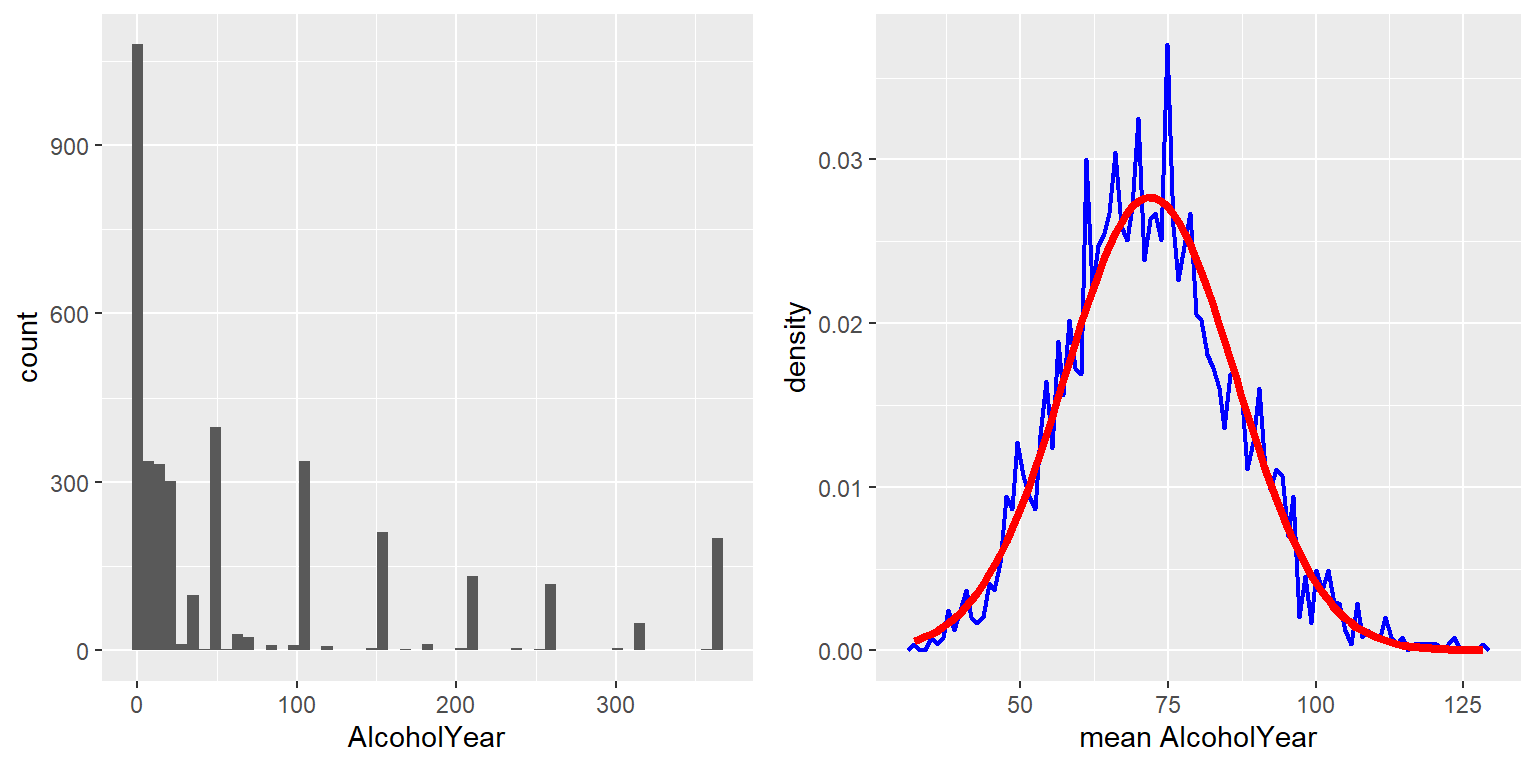
Figura 7.2: Izquierda: Distribución de la variable AlcoholYear en el conjunto de datos NHANES, la cual refleja el número de días que el individuo bebió en el año. Derecha: La distribución de muestreo de la media para AlcoholYear en el conjunto de datos NHANES, obtenido dibujando muestras repetidas de tamaño 50, en azul. La distribución normal con la misma media y misma desviación estándar está mostrada en rojo.
El teorema de límite central es importante para la estadística porque nos permite asumir con seguridad que la distribución de muestreo de la media va a ser normal en la mayoría de los casos. Esto significa que podemos tomar ventaja de las técnicas estadísticas que asumen una distribución normal, como veremos en la próxima sección. Es también importante porque nos dice por qué las distribuciones normales son tan comunes en el mundo real; siempre que combinamos factores diferentes en un solo número, el resultado muy probablemente será una distribución normal. Por ejemplo, la altura de cualquier adulto depende en una compleja mezcla de su genética y experiencia; incluso si las contribuciones individuales pueden no estar normalmente distribuidas, cuando las combinemos el resultado es una distribución normal.
7.5 Objetivos de aprendizaje
Al haber leído este capítulo, tu deberías de ser capaz de:
- Distinguir entre una población y una muestra, y entre parámetros de población y estadísticas de muestra
- Describir los conceptos de error muestral y distribución muestral.
- Calcular el error estándar de la media.
- Describir cómo el teorema del límite central determina la naturaleza de la distribución muestral de la media.
7.6 Lecturas sugeridas
- The Signal and the Noise: Why So Many Predictions Fail - But Some Don’t, por Nate Silver.