Capitulo 1 Introducción
“Algún día el pensamiento estadístico será tan necesario para la eficiencia ciudadana como la habilidad de leer y escribir” - H. G. Wells
1.1 ¿Qué es el pensamiento estadístico?
El pensamiento estadístico es una manera de entender el mundo complejo mediante la descripción relativamente simple en términos que capturen los aspectos esenciales de su estructura o su función, además de que nos provee con la idea de qué tanta incertidumbre tenemos sobre ese mismo conocimiento. Los fundamentos del pensamiento estadístico vienen principalmente de las matemáticas y estadística, sin embargo, también de las ciencias computacionales, psicología y otras áreas de estudio.
Podemos distinguir el pensamiento estadístico de otras formas de pensamiento que son menos probables de describir el mundo acertadamente. En particular, la intuición humana a menudo intenta responder las mismas preguntas que se pueden contestar con el pensamiento estadístico, pero frecuentemente de manera errónea. Por ejemplo, en años recientes la mayoría de lxs Americanxs han reportado que piensan que los crímenes violentos han empeorado en comparación con años previos (Pew Research Center). Sin embargo, un análisis estadístico de los datos de violencia criminal muestra que en realidad han ido disminuyendo paulatinamente desde la década de los noventas. La intuición falla porque dependemos de las mejores estimaciones o suposiciones (lo que lxs psicólogxs llaman heurística) que a menudo pueden equivocarse. Por ejemplo, las personas con frecuencia juzgan la prevalencia de algún evento (como el crimen violento) utilizando una heurística de disponibilidad – eso es, qué tan fácil podemos pensar en un ejemplo de crimen violento. Por esta razón, nuestros juicios del aumento de las tasas de violencia pueden ser más indicativas de un aumento en la cobertura de noticias, a pesar de una verdadera disminución en dicha tasa de crimen. El pensamiento estadístico nos provee de las herramientas para entender el mundo con más exactitud y superar los sesgos del juicio humano.
1.2 Lidiar con la ansiedad estadística
Muchas personas entran a su primera clase de estadística con mucho temor y ansiedad, especialmente una vez que escuchan que también van a tener que aprender código, a fin de analizar datos. En mi clase le doy a lxs estudientes una encuesta previa a la primera sesión de clase con la intención de medir su actitud hacia la estadística, pidiéndoles que califiquen un número de afirmaciones en una escala del 1 (totalmente en desacuerdo) a 7 (totalmente de acuerdo). Uno de los ítems en la encuesta es “El pensamiento de inscribirme a un curso de estadística me pone nerviosx.” En una clase reciente, casi dos tercios de la clase respondió con un cinco o más, y un cuarto de lxs estudiantes mencionó que estaban totalmente de acuerdo con la frase. Entonces si tú te sientes nerviosx acerca de empezar a aprender estadística, no estás solx.
La ansiedad se siente incómoda, pero la psicología nos dice que esta clase de respuesta emocional en realidad puede ayudarnos a desempeñarnos mejor en varias tareas, mediante focalizar nuestra atención. Así que si empiezas a sentirte ansiosx por el material en este libro, recuerda que muchxs otrxs leyendo esto se sienten de una manera similar y que esta respuesta emocional en realidad puede ayudarte a aprender mejor el material (¡incluso si no parece de esa manera!).
1.3 ¿Qué puede hacer la estadística por nosotrxs?
Hay tres principales cosas que podemos hacer con la estadística:
- Describir: El mundo es complejo y en ocasiones necesitamos describirlo en una manera simplificada en la que podamos entender.
- Decidir: En ocasiones necesitamos tomar decisiones basadas en datos, usualmente de cara a la incertidumbre.
- Predecir: En ocasiones deseamos hacer predicciones sobre nuevas situaciones basadas en nuestro conocimiento de situaciones previas.
Veamos un ejemplo de esto en acción, centrado en una pregunta en la que muchxs de nosotrxs estamos interesadxs: ¿Cómo decidimos qué es saludable al comer? Hay diferentes fuentes de guía; pautas alimentarias gubernamentales, libros dietéticos y bloggers, sólo por nombrar algunxs. Hay que enfocarnos en una pregunta específica: ¿La grasa saturada en nuestra dieta es algo malo?
Una manera en la que podemos responder esta pregunta es sentido común. Si comemos grasa, ésta se va a convertir en grasa en nuestro cuerpo, ¿cierto? Y todxs hemos visto fotos de arterias obstruidas con grasa, así que comer grasa va a obstruir nuestras arterias, ¿cierto?
Otra manera en la que podemos responder esta pregunta es mediante escuchar a figuras de autoridad. Las pautas alimenticias de la FDA (Food and Drug Administration, por sus siglas en inglés) tienen como una de sus recomendaciones clave que “Un patrón de comida saludable limita las grasas saturadas.” Uno esperaría que estas pautas estén basadas en ciencia, y en algunos casos es así, pero como Nina Teicholz señaló en su libro “Big Fat Surprise”(Teicholz 2014), esta recomendación en particular parece estar más basada en el antiguo dogma de investigadores de la nutrición que en evidencia actual.
Finalmente, podríamos revisar verdadera investigación científica. Empecemos por revisar el gran estudio llamado PURE Study (por sus siglas en inglés), el cual ha examinado dietas y resultados de salud (incluida la muerte) en más de 135,000 personas de 18 países diferentes. En uno de los análisis de esta base de datos (publicada en The Lancet en 2017; Dehghan et al. (2017)), lxs investigadores de PURE reportaron un análisis de cómo el consumo de varias clases de macronutrientes (incluidas las grasas saturadas y carbohidratos) estaba relacionada con la probabilidad de morir durante el tiempo en que se siguió a las personas. Las personas en el estudio fueron seguidas por una duración mediana de 7.4 años, significando que la mitad de las personas del estudio fueron seguidas por menos y la otra mitad fue seguida por más de 7.4 años. La Figura 1.1 grafica algunos de los datos del estudio (extraídos del documento), mostrando la relación entre el consumo de las grasas saturadas y carbohidratos y el riesgo de morir por cualquier causa.
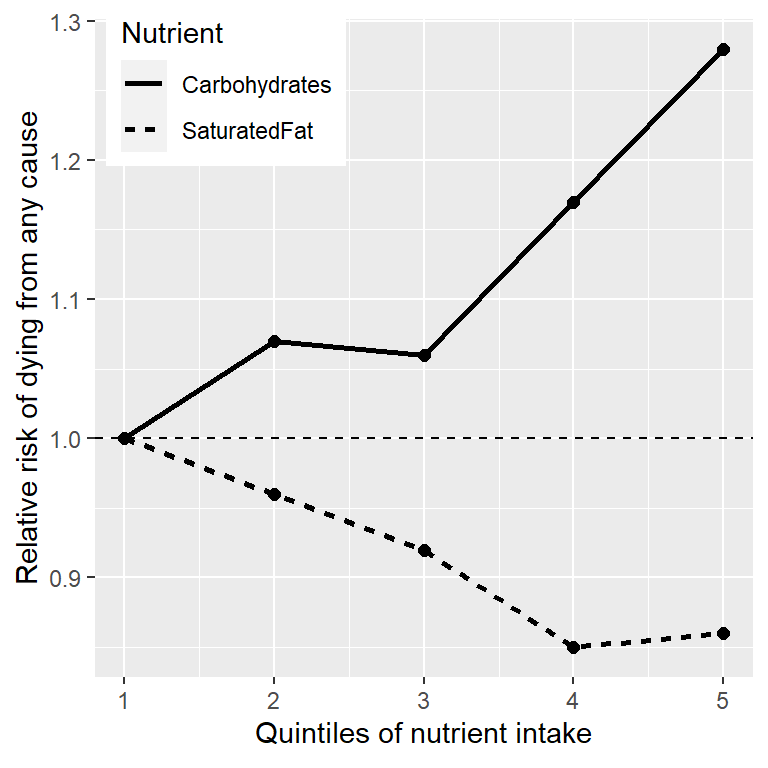
Figura 1.1: Una gráfica de datos del estudio PURE, mostrando la relación entre muerte debido a cualquier causa y la ingesta relativa de grasas saturadas y carbohidratos.
Esta gráfica está basada en diez números. Para obtener estos números, lxs investigadorxs dividieron al grupo de 135,335 participantes (al que llamaremos “muestra”) en 5 grupos (“quintiles”) después de haberlos ordenado en términos de su ingesta nutrimental; el primer quintil contiene el 20% de personas con la menor ingesta, y el 5to quintil contiene el 20% con la mayor ingesta. Lxs investigadorxs luego calcularon qué tan seguido las personas en cada uno de esos grupos había muerto durante el periodo que habían sido estudiadxs. La figura expresa esto en términos del riesgo relativo de morir en comparación al quintil menor: Si este número es mayor que uno, significa que las personas en ese grupo son más propensas a morir que las personas en el quintil menor, mientras que si es menor que uno, significa que las personas en este grupo son menos propensas a morir. La figura es bastante clara: Las personas que comieron más grasas saturadas tenían menor probabilidad de morir durante el estudio, con la menor tasa de muerte observada para las personas que estaban en el cuarto quintil (es decir, quienes comieron más grasa que el 60% más bajo pero menos que el 20% superior). Lo contrario fue observado en la ingesta de carbohidratos; la mayor cantidad de carbohidratos que una persona comió, la mayor probabilidad que tenían de morir durante el estudio. Este ejemplo muestra cómo podemos utilizar estadística para describir una compleja base de datos en términos mucho más sencillos con un conjunto de números; si tenemos que revisar los datos de cada participante del estudio al mismo tiempo, estaríamos saturadxs con datos y sería más complicado observar el patrón que emerge cuando son descritos de una manera más sencilla.
Los números en la Figura 1.1 parecen mostrar que las muertes disminuyen con la ingesta de grasas saturadas y aumentan con la ingesta de carbohidratos, pero también sabemos que hay mucha incertidumbre en los datos; hay algunas personas que murieron de manera prematura incluso si tenían una dieta baja en carbohidratos, y, de manera similar, algunas personas que comían muchísimos carbohidratos pero vivieron hasta una edad avanzada. Dada esta variabilidad, queremos decidir si las relaciones que vemos en los datos son lo sucifiente estrechas como para no esperar que ocurran al azar si no hubiera realmente una relación entre la dieta y la longevidad. La estadística nos provee con las herramientas para tomar este tipo de decisones, y a menudo las personas externas ven esto como el principal propósito de la estadística. Pero como veremos a lo largo del libro, esta necesidad de tomar decisiones en blanco y negro basadas en evidencias vagas a menudo ha llevado a lxs investigadores por mal camino.
Basándonos en los datos, también nos gustaría hacer predicciones sobre resultados futuros. Por ejemplo, es posible que una compañía de seguros de vida desee usar datos sobre la ingesta de grasas y carbohidratos de una persona en particular para predecir cuánto tiempo es probable que viva. Un aspecto importante de la predicción es que requiere que generalicemos a partir de los datos que ya tenemos a alguna otra situación, a menudo en el futuro; si nuestras conclusiones se limitaran a las personas específicas del estudio en un momento determinado, entonces el estudio no sería muy útil. En general, lxs investigadorxs deben asumir que su muestra particular es representativa de una población más grande, lo que requiere que obtengan la muestra de una manera que proporcione una imagen no sesgada de la población. Por ejemplo, si el estudio PURE hubiera reclutado a todos sus participantes de sectas religiosas que practican el vegetarianismo, probablemente no querríamos generalizar los resultados a personas que siguen diferentes estándares dietéticos.
1.4 Las grandes ideas de la estadística
Hay un número de ideas sumamente básicas que interceptan casi todos los aspectos del pensamiento estadístico. Algunas de ellas son señaladas por (Stigler 2016) en su increíble libro “Los Siete Pilares de la Sabiduría Estadística,”las cuales he ampliado aquí.
1.4.1 Aprender de los datos
Una forma de pensar en la estadística es como un conjunto de herramientas que nos permiten aprender de los datos. En cualquier situación, comenzamos con un conjunto de ideas o hipótesis sobre cuál podría ser el caso. En el estudio PURE, lxs investigadorxs pueden haber comenzado con la expectativa de que comer más grasa conduciría a tasas de mortalidad más altas, dado el dogma negativo predominante sobre las grasas saturadas. Más adelante en el curso presentaremos la idea de conocimiento previo, que pretende reflejar el conocimiento que aportamos a una situación. Este conocimiento previo puede variar en su fuerza, a menudo basado en nuestra cantidad de experiencia; si visito un restaurante por primera vez, es probable que tenga una expectativa débil de lo bueno que será, pero si visito un restaurante donde he comido diez veces antes, mis expectativas serán mucho más fuertes. De manera similar, si miro un sitio de reseñas de restaurantes y veo que la calificación promedio de un restaurante de cuatro estrellas se basa solo en tres reseñas, tendré una expectativa más débil de la que tendría si se basara en 300 reseñas.
La estadística nos proporciona una manera de describir cómo se pueden utilizar mejor los nuevos datos para actualizar nuestras creencias y, de esta manera, existen vínculos profundos entre la estadística y la psicología. De hecho, muchas teorías del aprendizaje humano y animal de la psicología están estrechamente alineadas con ideas del nuevo campo del aprendizaje automático (machine learning). El aprendizaje automático es un campo en la interfaz de las estadísticas y la informática que se centra en cómo construir algoritmos informáticos que puedan aprender de la experiencia. Si bien las estadísticas y el aprendizaje automático a menudo intentan resolver los mismos problemas, los investigadores de estos campos suelen adoptar enfoques muy diferentes; el famoso estadístico Leo Breiman una vez se refirió a ellos como “Las dos culturas” para reflejar cuán diferentes pueden ser sus enfoques (Breiman 2001). En este libro intentaré combinar las dos culturas porque ambos enfoques proporcionan herramientas útiles para pensar en los datos.
1.4.2 Agregación (aggregation)
Otra manera de pensar en la estadística es como “la ciencia de tirar datos.” En el ejemplo anterior del estudio PURE, tomamos más de 100,000 números y los condensamos a diez. Es esta clase de agregación la que es uno de los conceptos más importantes de la estadística. Cuando fue desarrollado por primera vez, fue revolucionario: si descartamos todos los detalles sobre cada uno de lxs participantes, ¿cómo podemos estar seguros de que no nos estamos perdiendo algo importante?
Como veremos, la estadística nos proporciona formas de caracterizar la estructura de agregados de datos, con fundamentos teóricos que explican por qué esto suele funcionar bien. Sin embargo, también es importante tener en cuenta que la agregación puede ir demasiado lejos, y más adelante encontraremos casos en los que un resumen puede proporcionar una imagen muy engañosa de los datos que están siendo resumidos.
1.4.3 Incertidumbre
El mundo es un lugar incierto. Ahora sabemos que fumar cigarrillos causa cáncer de pulmón, pero esta causa es probabilística: un hombre de 68 años que ha fumado dos paquetes al día durante los últimos 50 años y sigue fumando tiene un riesgo del 15% (1 de cada 7) de contraer cáncer de pulmón, que es mucho mayor que la probabilidad de cáncer de pulmón en una persona que no fuma. Sin embargo, también significa que habrá muchas personas que fumarán durante toda su vida y nunca tendrán cáncer de pulmón. La estadística nos proporciona las herramientas para caracterizar la incertidumbre, tomar decisiones en condiciones de incertidumbre y realizar predicciones cuya incertidumbre podemos cuantificar.
A menudo se ve a lxs periodistas escribir que lxs investigadorxs científicxs han “probado” algunas hipótesis. Pero el análisis estadístico nunca puede “probar” una hipótesis, en el sentido de demostrar que debe ser verdadera (como se haría en una prueba lógica o matemática). La estadística puede proporcionarnos evidencias, pero siempre son provisionales y están sujetas a la incertidumbre que siempre está presente en el mundo real.
1.4.4 Muestrear de una población
El concepto de agregación implica que podemos obtener información útil al colapsar los datos, pero ¿cuántos datos necesitamos? La idea de muestreo dice que podemos resumir una población completa basándonos en solo una pequeña cantidad de muestras de la población, siempre que esas muestras se obtengan de la manera correcta. Por ejemplo, el estudio PURE inscribió una muestra de aproximadamente 135,000 personas, pero su objetivo era proporcionar información sobre los miles de millones de seres humanos que componen la población de la que se tomaron muestras. Como ya comentamos anteriormente, la forma en que se obtiene la muestra del estudio es fundamental, ya que determina qué tan ampliamente podemos generalizar los resultados. Otra idea fundamental sobre el muestreo es que, si bien las muestras más grandes son siempre mejores (en términos de su capacidad para representar con precisión a toda la población), hay rendimientos decrecientes a medida que la muestra aumenta. De hecho, la velocidad a la que disminuye el beneficio de muestras más grandes sigue una regla matemática simple, que crece como la raíz cuadrada del tamaño de la muestra, de modo que para duplicar la calidad de nuestros datos necesitamos cuadriplicar el tamaño de nuestra muestra.
1.5 Causalidad y estadística
El estudio PURE pareció proporcionar pruebas bastante sólidas de una relación positiva entre comer grasas saturadas y vivir más tiempo, pero esto no nos dice lo que realmente queremos saber: si comemos más grasas saturadas, ¿nos hará vivir más tiempo? Esto se debe a que no sabemos si existe una relación causal directa entre comer grasas saturadas y vivir más tiempo. Los datos son consistentes con tal relación, pero son igualmente consistentes con algún otro factor que cause tanto una mayor ingesta de grasas saturadas como una vida más larga. Por ejemplo, es probable que las personas que son más ricas consuman más grasas saturadas y las personas más ricas tienden a vivir más tiempo, pero su vida más larga no se debe necesariamente a la ingesta de grasas, sino que podría deberse a una mejor atención de la salud, una reducción del estrés psicológico, mejor calidad de los alimentos o muchos otros factores. Los investigadores del estudio PURE intentaron tener en cuenta estos factores, pero no podemos estar seguros de que sus esfuerzos eliminaron por completo los efectos de otras variables. El hecho de que otros factores puedan explicar la relación entre la ingesta de grasas saturadas y la muerte es un ejemplo de por qué las clases de introducción a la estadística a menudo enseñan que “la correlación no implica causalidad,” aunque el renombrado experto en visualización de datos Edward Tufte ha agregado, “pero seguro que es una pista.”
Aunque la investigación observacional (como el estudio PURE) no puede demostrar de manera concluyente relaciones causales, generalmente pensamos que la causalidad se puede demostrar utilizando estudios que controlan y manipulan experimentalmente un factor específico. En medicina, este tipo de estudio se conoce como ensayo controlado aleatorio (ECA, en inglés randomized controlled trial, RCT). Digamos que queríamos hacer un ECA para examinar si el aumentar la ingesta de grasas saturadas aumenta la esperanza de vida. Para hacer esto, tomaríamos muestras de un grupo de personas y luego las asignaríamos a un grupo de tratamiento (al que se le indicaría que aumentara su ingesta de grasas saturadas) o un grupo de control (al que se le diría que siguiera comiendo lo mismo que antes) . Es fundamental que asignemos a los individuos a estos grupos al azar. De lo contrario, las personas que eligen el tratamiento pudieran ser diferentes de alguna manera a las personas que eligen el grupo de control – por ejemplo, pudiera ser más probable que también adopten otros comportamientos saludables. Luego seguiríamos a los participantes a lo largo del tiempo y veríamos cuántas personas de cada grupo murieron. Debido a que asignamos al azar a los participantes a los grupos de tratamiento o de control, podemos estar razonablemente seguros de que no hay otras diferencias entre los grupos que pudieran confundir el efecto del tratamiento; sin embargo, todavía no podemos estar seguros porque a veces la aleatorización produce grupos de tratamiento versus grupos de control que varían de alguna manera importante. Lxs investigadores a menudo intentan abordar estos factores de confusión mediante análisis estadísticos, pero eliminar la influencia de un factor de confusión de los datos puede resultar muy difícil.
Varios ECA han examinado la cuestión de si cambiar la ingesta de grasas saturadas da como resultado una mejor salud y una vida más larga. Estos ensayos se han centrado en reducir las grasas saturadas debido al fuerte dogma entre los investigadores en nutrición de que las grasas saturadas son mortales; la mayoría de estos investigadores probablemente habrían argumentado que no era ético hacer que las personas comieran más grasas saturadas. Sin embargo, los ECA han mostrado un patrón muy consistente: en general, no hay un efecto apreciable sobre las tasas de muerte al reducir la ingesta de grasas saturadas.
1.6 Objetivos de aprendizaje
Al leer este capítulo, deberías de ser capaz de:
- Describir los objetivos centrales y conceptos fundamentales de la estadística.
- Describir la diferencia entre investigación experimental y observacional con respecto a lo que puede inferir sobre la causalidad.
- Explicar cómo la aleatorización nos provee de la habilidad para hacer inferencias acerca de la causalidad.
1.7 Lecturas sugeridas
- The Seven Pillars of Statistical Wisdom, por Stephen Stigler.
- The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century, por David Salsburg.
- Naked Statistics: Stripping the Dread from the Data, por Charles Wheelan.