Capitulo 5 Ajustar modelos a datos

Una de las actividades fundamentales en estadística es crear modelos que puedan resumir datos utilizando un grupo pequeño de números, de esta forma, se provee una descripción compacta de los datos. En este capítulo discutiremos el concepto de lo que es un modelo estadístico y cómo puede ser utilizado para describir datos.

5.1 ¿Qué es un modelo?

En el mundo físico, los “modelos” son generalmente simplificaciones de cosas del mundo real que, no obstante, transmiten la esencia de lo que se está modelando. El modelo de un edificio transmite la escencia de la estructura del edificio mientras es lo suficientemente pequeño y ligero como para que unx lo pueda sostener con las manos; un modelo de una célula de biología es mucho más grande que una célula real, no obstante, transmite la mayoría de las partes de la célula y las relaciones que tienen entre sí.

En estadística, un modelo tiene el propósito de proveer una descripción similar condensada, pero para los datos, en lugar de una estructura física. Como los modelos físicos, un modelo estadístico es generalmente mucho más simple que los datos que están siendo descritos; tiene el propósito de capturar la estructura de los datos de la forma más simple posible. En ambos casos, podemos notar que el modelo es una ficción conveniente que necesariamente pasa por alto algunos detalles de lo que está tratando de representar. Como el estadístico George Box dijo: “Todos los modelos son incorrectos, pero algunos son útiles.” También puede ser útil el pensar en un modelo estadístico como una teoría sobre cómo se generaron los datos observados; nuestra meta entonces se convierte en encontrar el modelo que de manera más eficiente y precisa resume la manera en que los datos fueron generados realmente. Pero como veremos más abajo, los deseos de eficiencia y precisión frecuentemente se opondrán diametralmente el uno al otro.

La estructura básica de un modelo estadístico es:

\[ Datos= modelo + error \] Esto expresa la idea de que los datos pueden ser partidos en dos porciones: una porción descrita por un modelo estadístico, el cual expresa los valores que esperamos que tengan los datos dado nuestro conocimiento, y otra porción que denominamos como error, que refleja la diferencia entre las predicciones del modelo y los datos observados.

En esencia, nos gustaría usar nuestro modelo para predecir los valores de los datos para cada observación. Escribiríamos la ecuación de la siguiente manera:

\[ \widehat{dato_i} = modelo_i \] El “sombrero” sobre el “dato” denota que es nuestra predicción, en lugar del valor real de nuestro dato. Esta ecuación significa que el valor predicho para el dato de la observación \(i\) es igual al valor del modelo para esa misma observación. Una vez que tenemos una predicción desde nuestro modelo, podemos calcular el error:

\[ error_i = dato_i - \widehat{dato_i} \] Esto es, el error en cualquier observación es la diferencia entre el valor observado del dato y el valor predicho para ese dato desde el modelo.

5.2 Modelado estadístico: Un ejemplo

Observemos un ejemplo de construir un modelo para un conjunto de datos, utilizando los datos de NHANES. En particular, trataremos de construir un modelo de la altura de lxs niñxs en la muestra de NHANES. Primero vamos a cargar los datos y los graficaremos (ve la Figura 5.1).

<– fig.cap=“Histogram of height of children in NHANES.” –>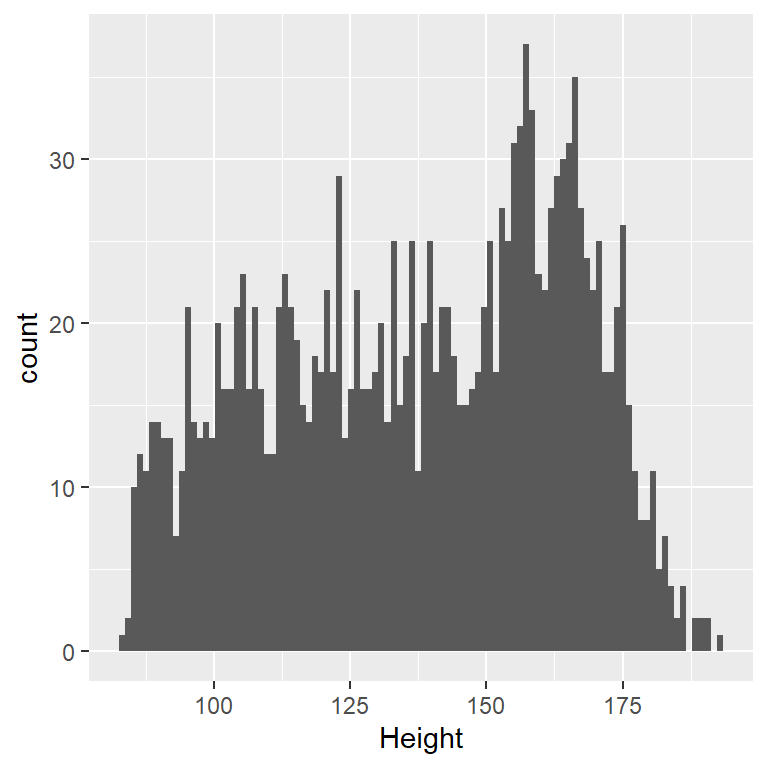

Figura 5.1: Histograma de la altura de lxs niñxs en NHANES.

Recuerda que queremos describir los datos de la forma más simple posible mientras que al mismo tiempo capturamos sus características más importantes. El modelo más simple que podemos imaginar involucraría un solo número; esto es, el modelo predeciría el mismo valor para cada observación, sin importar qué más cosas podamos saber acerca de estas observaciones. Generalmente describimos un modelo en términos de sus parámetros, que son valores que podemos cambiar para modificar las predicciones del modelo. A lo largo de este libro, nos referiremos a estos parámetros usando la letra griega beta (\(\beta\)); cuando el modelo tiene más de un parámetro, usamos números en subíndices para denotar diferentes betas (por ejemplo, \(\beta_1\)). La costumbre también es referirnos a los valores de los datos usando la letra \(y\), y usar los subíndices \(y_i\) para referirnos a las observaciones individuales.

Generalmente no sabemos los verdaderos valores de los parámetros, por lo que tenemos que estimarlos a partir de los datos. Por esta razón, generalmente le pondremos un “sombrero” sobre los símbolos de los \(\beta\) para denotar que estamos usando una estimación del valor del parámetro en lugar de su valor verdadero (el cual generalmente no sabemos). Por lo tanto, el modelo más simple para los datos de la altura usando un solo parámetro sería:

\[ y_i = \hat{\beta} + \epsilon \]

El subíndice \(i\) no aparece en el lado derecho de la ecuación, lo que significa que la predicción del modelo no depende de cuál observación estamos revisando — es la misma predicción para todas las observaciones. La pregunta entonces se convierte en: ¿Cómo podemos estimar los mejores valores de los parámetros del modelo? En este caso en particular, ¿cuál valor individual es la mejor estimación de \(\beta\)? Y de manera aún más importante, ¿cómo definimos lo que es mejor?

Una estimación muy simple que nos podemos imaginar es la moda, que es simplemente el valor más común entre los datos. Esto redefine el conjunto de 1691 niñxs en términos de un solo número. Si quisiéramos predecir la altura de nuevos niñxs, entonces nuestro valor predicho sería el mismo número:

\[ \hat{y_i} = 166.5 \]

El error para cada persona sería entonces la diferencia entre el valor predicho (\(\hat{y_i}\)) y su altura real (\(y_i\)):

\[ error_i = y_i - \hat{y_i} \]

¿Qué tan bueno es este modelo? En general definimos qué tan bueno es un modelo en términos de la magnitud del error, el cual representa el grado en que los datos difieren de las predicciones del modelo; todas las cosas siendo iguales, el modelo que produce el error menor es el mejor modelo. (Aunque, como revisaremos más adelante, todas las cosas usualmente no son iguales…). Lo que encontramos en este caso es que la persona promedio tiene un error bastante grande de -28.8 centímetros cuando usamos la moda como nuestra estimación de \(\beta\), lo que no se ve nada bien a simple vista.

¿Cómo podríamos encontrar una mejor estimación para el parámetro de nuestro modelo? Podemos comenzar tratando de encontrar un estimador que nos brinde un promedio de los errores de cero. Un buen candidato es la media aritmética (esto es, el promedio, usualmente representado con una barra sobre la variable, como por ejemplo \(\bar{X}\)), que se calcula al sumar todos los valores y luego dividirlos entre el número de valores. Matemáticamente, lo expresamos así:

\[ \bar{X} = \frac{\sum_{i=1}^{n}x_i}{n} \]

Resulta que si usamos la media aritmética como nuestro estimador, entonces el promedio de error efectivamente será cero (mira la prueba al final de este capítulo si estás interesadx). Aunque el promedio de error sobre la media es cero, podemos observar en el histograma en la Figura 5.2 que cada persona aún tiene algún grado de error; algunos errores son positivos y otros son negativos, por lo que se terminan cancelando entre sí dando un promedio de error igual a cero.

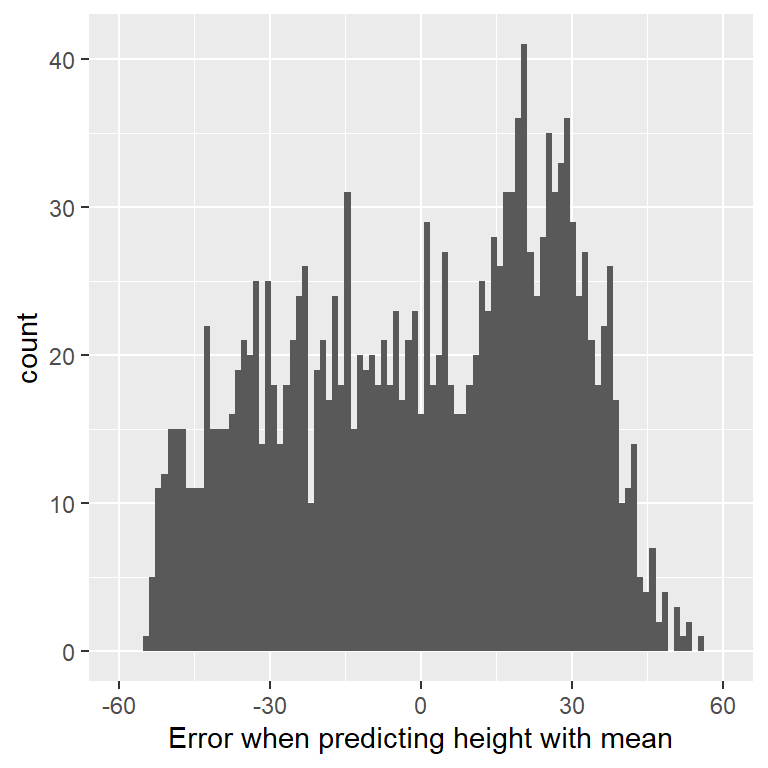
Figura 5.2: Distribución de errores a partir de la media.

El hecho de que los errores positivos y negativos se cancelen entre sí significa que dos modelos diferentes podrían tener errores de diferentes magnitudes en términos absolutos, pero tendrían el mismo error promedio. Es exactamente por esta razón por la que el error promedio no es un buen criterio para evaluar nuestro estimador; queremos un criterio que intente minimizar el error total, sin importar su dirección. Por esta razón, generalmente resumimos los errores en términos de algún tipo de medición que considera tanto los errores positivos como los negativos como malos. Podríamos usar el valor absoluto de cada error, pero es más común usar los errores al cuadrado, por razones que veremos después en el libro.

Existen varias formas comunes para resumir el error al cuadrado con el que te encontrarás en varios puntos de este libro, por lo que es importante comprender cómo se relacionan entre ellos. En primer instancia, podríamos simplemente sumarlos; esto se conoce como la suma de los errores al cuadrado (sum of squared errors). La razón por la que usualmente no utilizamos este método es porque su magnitud depende del número de datos, por lo que puede ser difícil de interpretar a menos que estemos viendo el mismo número de observaciones. En segundo lugar, podríamos tomar la media de los valores de error al cuadrado, lo cual se conoce como error cuadrático medio (MSE por sus siglas en inglés: mean squared error). Sin embargo, ya que elevamos al cuadrado los valores antes de promediarlos, no están en la misma escala que los datos originales; están en \(centímetros^2\). Por esta razón, también es común tomar la raíz cuadrada del error cuadrático medio, al cual nos referimos como raíz del error cuadrático medio (RMSE por sus siglas en inglés: root mean squared error), para que el error sea medido en las mismas unidades que los valores originales (en este ejemplo, centímetros).

La media contiene una cantidad sustancial de error – cualquier punto individual en los datos estará a unos 27 cm de la media en promedio – pero aún así es mucho mejor que la moda, la cual tiene una raíz de error cuadrático medio de unos 39 cm.

5.2.1 Mejorando nuestro modelo

¿Podemos imaginar un mejor modelo? Recuerda que estos datos son de todxs lxs niñxs en la muestra NHANES, quienes varían de 2 a 17 años de edad. Dado este amplio rango de edades, esperaríamos que nuestro modelo de estatura también incluyera edad. Grafiquemos los datos de estatura frente a la edad, para ver si realmente existe relación.

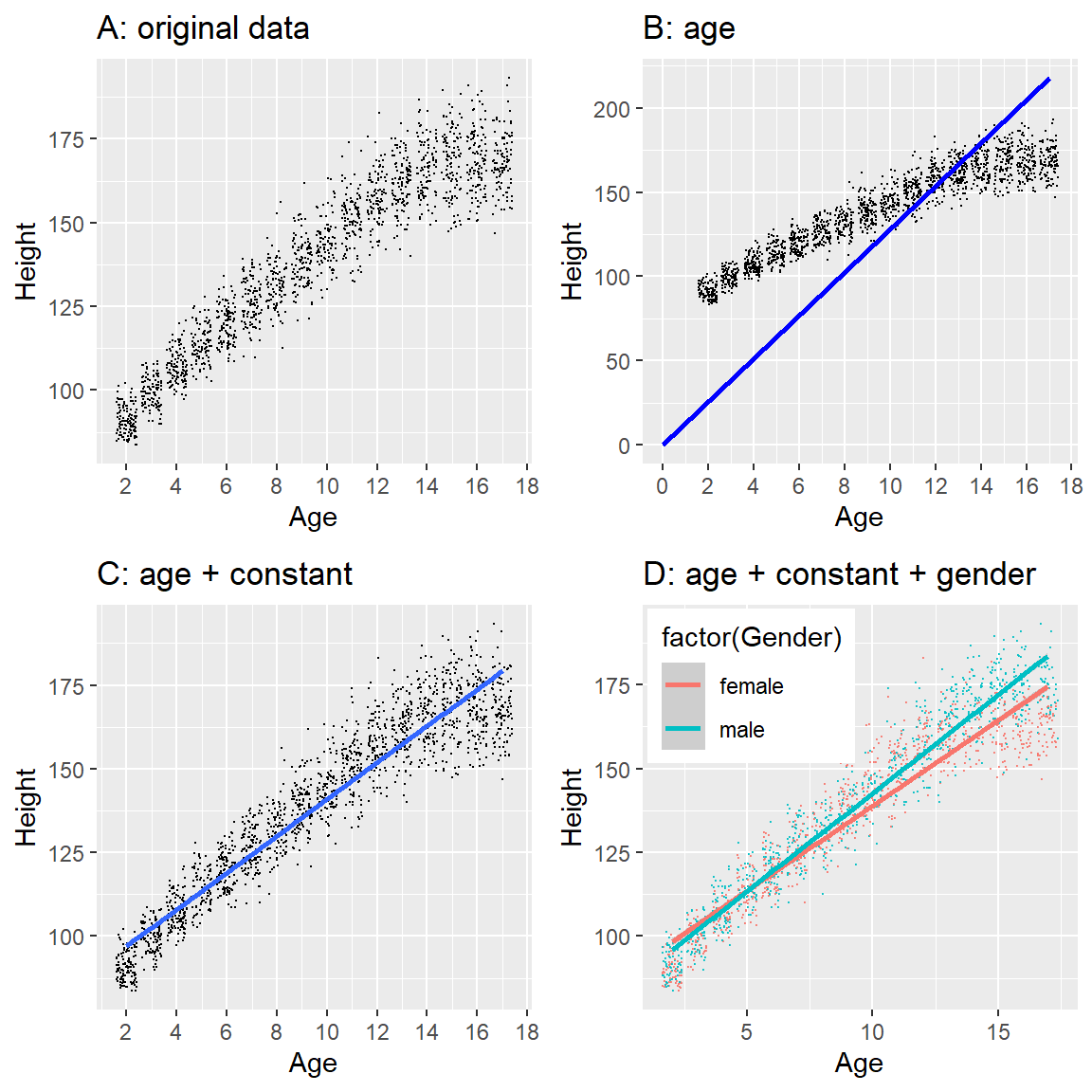
Figura 5.3: Altura de lxs niñxs en NHANES, graficada sin un modelo (A), con un modelo lineal que incluye sólo edad (B) o edad y una constante (C), y con un modelo lineal que ajusta efectos separados de la edad para niños y niñas (D).

Los puntos negros en el Panel A de la Figura 5.3 muestran personas individuales en el grupo de datos, y parece ser que hay una relación fuerte entre la edad y la estatura, como esperaríamos. Por lo que esperaríamos poder construir un modelo que relacione estatura y edad:

\[ \hat{y_i} = \hat{\beta} * age_i \]

donde \(\hat{\beta}\) es nuestra estimación del parámetro que multiplicamos por edad para generar la predicción del modelo.

Puede que recuerdes de álgebra que una línea se define de la siguiente manera:

\[ y = pendiente*x + constante \]

Si la edad es la variable \(X\), eso quiere decir que nuestra predicción de la altura conforme a la edad será una línea con una pendiente de \(\beta\) y una constante de cero. Para observar esto, tracemos una línea azul que mejor se acomode sobre los datos (Panel B en Figura 5.3). Algo está claramente mal con este modelo, ya que, la linea no parece seguir los datos muy bien. De hecho, ¡el RMSE para este modelo (39.16) es más alto que el modelo que solamente incluye la media! El problema radica en el hecho de que nuestro modelo solamente incluye la edad, lo cual significa que el valor de la altura predicho por el modelo debe tomar un valor de cero cuando la edad es cero. Aunque los datos no incluyen niñxs con edad de cero, la línea requiere matemáticamente tener un valor “y” de cero cuando “X” es cero, lo cual explica por qué la línea es jalada por debajo de los puntos de datos más bajos (o jóvenes). Podemos arreglar esto al incluir una constante (intercept) en nuestro modelo, lo cual básicamente representa una altura estimada cuando la edad es igual a cero; aunque una edad de cero no es plausible en este conjunto de datos, este es un truco matemático que permitirá que el modelo tenga en cuenta la magnitud general de los datos.

\[ \widehat{y_i} = \hat{\beta_0} + \hat{\beta_1} * edad_i \]

donde \(\hat{\beta_0}\) es nuestra estimación para la constante (intercept), el cual es un valor constante agregado a la predicción para cada persona; lo llamamos constante porque se mapea en la constante (o intercept) en la ecuación de la línea recta (la altura en \(y\) por la que cruza la línea cuando x es igual a cero). Más adelante aprenderemos cómo es que realmente estimamos estos valores de parámetros para un conjunto de datos en particular; por ahora, usaremos nuestro software estadístico para estimar los valores de los parámetros que nos den el error más pequeño para este conjunto de datos en particular. El Panel C en la Figura 5.3 muestra este modelo aplicado a los datos de NHANES, en donde podemos observar que la línea coincide mucho mejor con los datos que la que no tiene constante.

Nuestro error es mucho más pequeño utilizando este modelo – sólo 8.36 centímetros en promedio. ¿Puedes pensar en otras variables que también se relacionen con la estatura? ¿Qué hay del género? En el Panel D de la Figura 5.3 graficamos los datos con líneas distintas para género masculino y femenino. Observando sólo la gráfica, parece ser que existe una diferencia entre género masculino y femenino, pero es relativamente pequeño y solamente comienza después de la etapa de la pubertad. En la Figura 5.4 trazamos los valores de la raíz del error cuadrático medio a través de los diferentes modelos, incluyendo un modelo más que tiene un parámetro adicional que modela el efecto del género. Aquí podemos ver que el modelo mejoró un poco al pasar de moda a media, posteriormente mejora más al pasar de media a media + edad, y mejora sólo un poco más al incluir el género también.

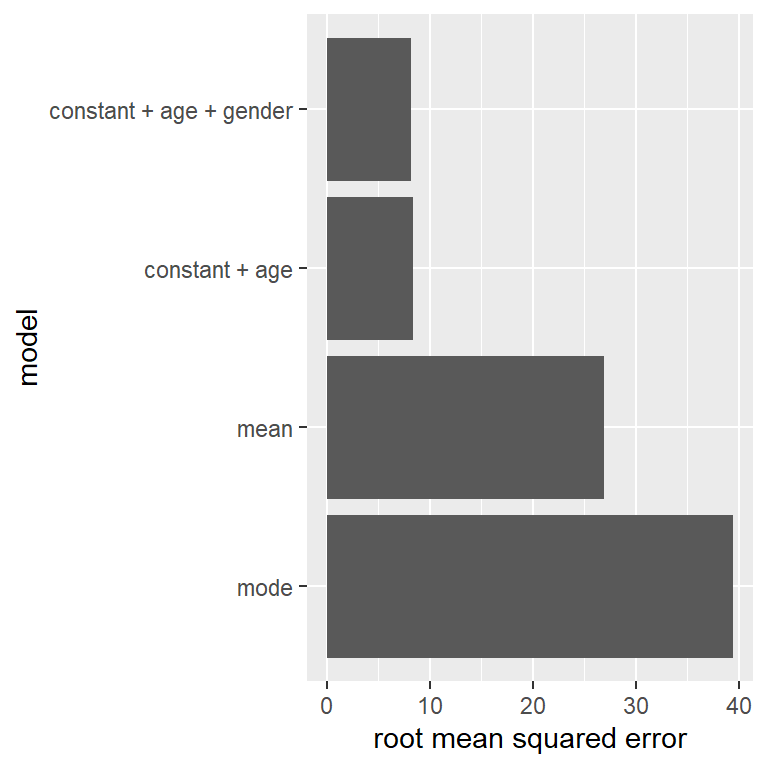
Figura 5.4: Error cuadrático medio graficado para cada uno de los modelos probados arriba.

5.3 ¿Qué hace que un modelo sea “bueno?”

Generalmente hay dos cosas diferentes que queremos de nuestro modelo estadístico. En primer lugar, queremos que describa nuestros datos correctamente; es decir, queremos que tenga el menor error posible cuando modelemos nuestros datos. En segundo lugar, queremos que se generalice bien a nuevas agrupaciones de datos; es decir, queremos que su error sea lo más bajo posible cuando lo apliquemos a una nueva agrupación de datos para poder hacer una predicción. Resulta ser que estas dos características se encuentran en conflicto constantemente.

Para entender esto, pensemos de dónde viene el error. Puede ocurrir si nuestro modelo está mal, por ejemplo, si de manera incorrecta afirmáramos que la altura declina conforme unx va creciendo en edad, en lugar de decir que la altura crece conforme a unx va cumpliendo más años. En este caso, nuestro error será mucho mayor de lo que sería con el modelo correcto. Similarmente, si hay un factor importante que le hace falta a nuestro modelo, esto también aumentará nuestro error (como ocurrió cuando dejamos de lado la edad para el modelo que generamos para la altura). De cualquier forma, un error también puede ocurrir cuando el modelo es correcto, debido a una posible variación aleatoria en los datos, a la cual solemos referirnos como “error de medición” o “ruido.” A veces esto se debe a un error en nuestra medición – por ejemplo, cuando la medición está bajo el cargo de unx humanx, al usar un cronómetro para medir tiempo transcurrido en una carrera a pie. En otros casos nuestra herramienta de medición puede ser muy exacta (como una escala digital para calcular el peso corporal), pero aquello que está siendo medido puede ser afectado por diversos factores que hacen que varíe. Si conociéramos todos estos factores, entonces podríamos generar un modelo más exacto, pero la realidad es que eso es raramente posible.

Usemos un ejemplo para ilustrar esto. En lugar de utilizar datos reales, generaremos datos para este ejemplo utilizando una simulación por computadora (de la cual hablaremos más adelante en los siguientes capítulos). Digamos que queremos comprender la relación entre el contenido de alcohol en la sangre (“BAC” por sus siglas en inglés: blood alcohol content) y su tiempo de reacción en una prueba de conducir simulada. Podemos generar algunos datos simulados y graficar la relación (ver Panel A de la Figura 5.5).

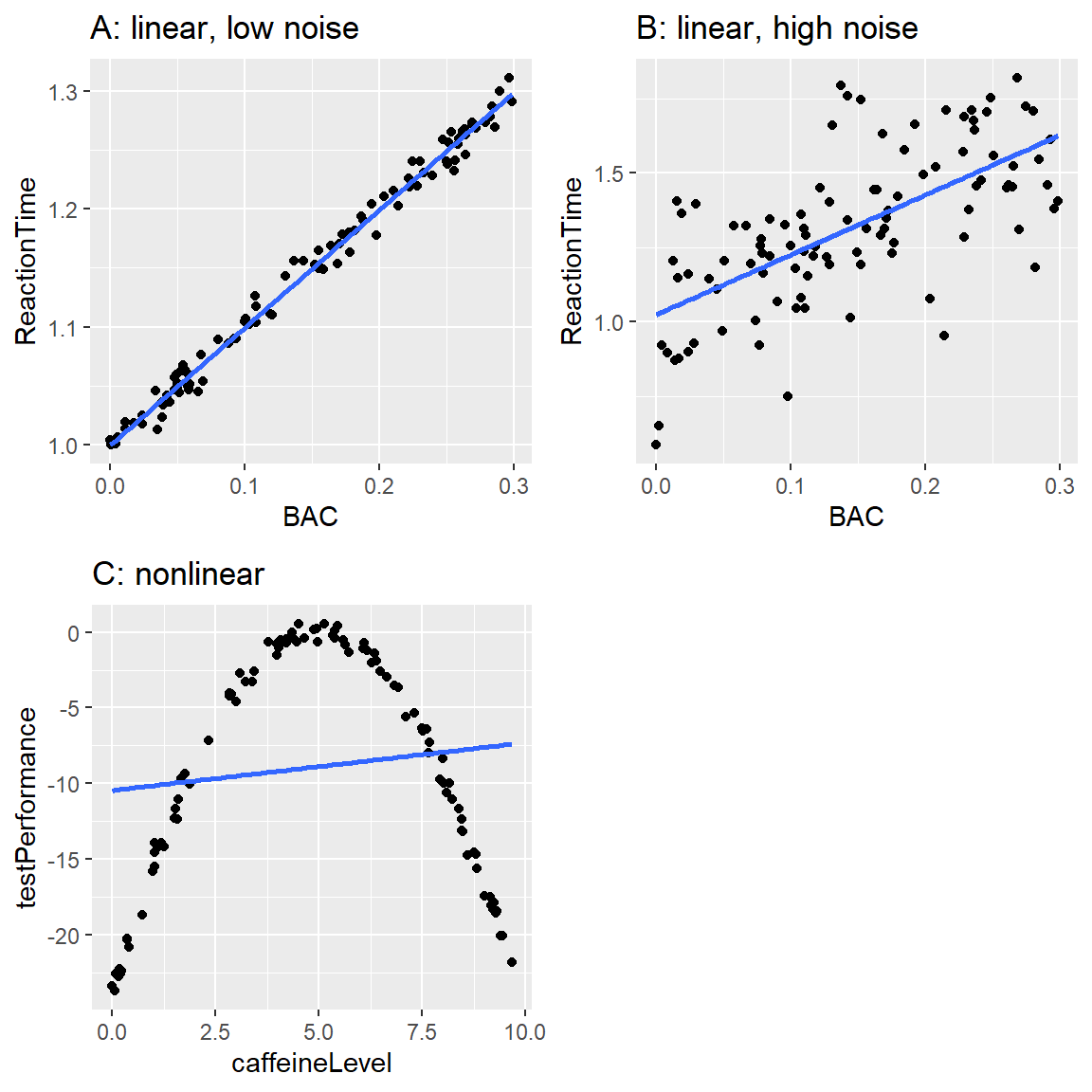
Figura 5.5: Relación simulada entre contenido de alcohol en la sangre y tiempo de reacción en una prueba de manejo, con el mejor modelo lineal ajustado representado por la línea. A: relación lineal con bajo error de medición. B: relación lineal con alto error de medición. C: relación no-lineal con bajo error de medición y un modelo lineal ajustado (incorrectamente).

En este ejemplo, el tiempo de reacción sube sistemáticamente con el contenido de alcohol en la sangre – la línea muestra el modelo más adecuado, y podemos ver que hay un margen de error pequeño, el cual se evidencia en el hecho de que todos los puntos están muy cerca de la línea.

También podemos pensar en datos que muestren la misma relación linear, pero que tengan un mayor margen de error, como en el Panel B de la Figura 5.5. Aquí podemos ver que aún hay un incremento sistemático del tiempo de reacción con el contenido de alcohol en la sangre (BAC), pero es mucho más variable a lo largo de lxs individuos.

Estos fueron dos ejemplos en donde la relación entre las dos variables parece ser lineal, y el error refleja ruido en nuestra medición. Por otro lado, hay otras situaciones en donde la relación entre las variables no es lineal, y el error va a incrementarse porque el modelo no está correctamente especificado. Digamos que estamos interesadxs en la relación entre la ingesta de cafeína y el rendimiento en un examen. La relación entre estimulantes como la cafeína y el rendimiento en un examen es a menudo no lineal - esto quiere decir que no sigue una línea recta. Esto es porque el rendimiento sube con cantidades pequeñas de cafeína (conforme la persona se pone más alerta), pero después empieza a declinar con cantidades grandes (conforme la persona se pone más nerviosa). Podemos simular datos de esta forma, y luego ajustar un modelo lineal a los datos (observa el Panel C de la Figura 5.5). La línea azul muestra la línea recta que mejor se ajusta a estos datos; claramente, hay un alto margen de error. Aunque existe una relación entre el rendimiento de la prueba y la ingesta de cafeína, sigue a una curva en lugar de a una línea recta. El modelo que asume una relación lineal tiene mayor error porque es el modelo incorrecto para este tipo de datos.

5.4 ¿Un modelo puede ser demasiado bueno?

Un error suena como algo malo, y usualmente vamos a preferir un modelo que tenga menor error a uno que tenga mayor error. No obstante, ya mencionamos que existe tensión entre la habilidad de un modelo para ajustarse correctamente a un conjunto de datos en particular y su habilidad para generalizarse a nuevos conjuntos de datos, ¡y resulta ser que el modelo con el menor error es a menudo peor para generalizarse a nuevos conjuntos de datos!

Para ver esto, hay que generar de nuevo un conjunto de datos para que podamos conocer la verdadera relación entre las variables. Crearemos dos conjuntos de datos simulados, los cuales se generarán de la misma manera exacta – solamente que van a tener diferente ruido aleatorio añadido a ellos. Esto es, la ecuación para ambos conjuntos de datos es \(y = \beta * X + \epsilon\); la única diferencia está en que se usó diferente ruido aleatorio para \(\epsilon\) en cada caso.

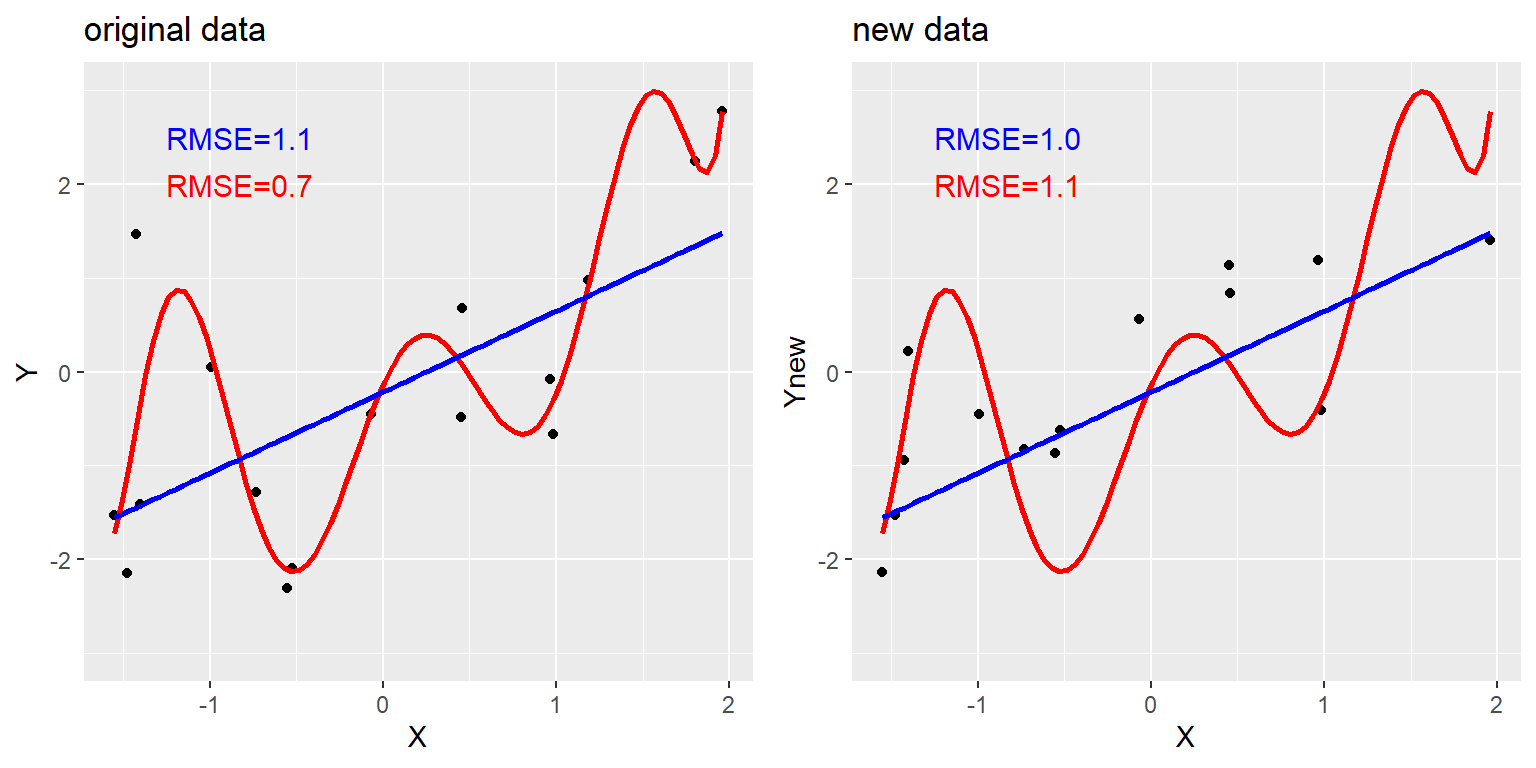
Figura 5.6: Un ejemplo de sobreajuste (overfitting). Ambos conjuntos de datos fueron generados usando el mismo modelo, con diferente ruido aleatorio añadido al generar cada conjunto. El panel izquierdo muestra los datos usados para ajustar el modelo, con un modelo lineal simple en azul y un modelo complejo (polinomial de 8vo orden) en rojo. Los valores de la raíz cuadrada del error cuadrático medio (RMSE, root mean square error) de cada modelo se muestran en la figura; en este caso, el modelo complejo tiene menor RMSE que el modelo simple. El panel de la derecha muestra el segundo conjunto de datos, con el mismo modelo sobrepuesto y los valores RMSE calculados usando usando el modelo obtenido del primer conjunto de datos. Aquí vemos que el modelo más simple ajustar mejor a los nuevos datos que el modelo más complejo, el cual había sido sobreajustado (overfitted) al primer conjunto de datos.

El panel de la izquierda en la Figura 5.6 muestra que el modelo más complejo (en rojo) se ajusta a los datos mejor que el modelo simple (en azul) generado en la misma manera– aquí podemos observar que el modelo más simple se ajusta mejor al nuevo conjunto de datos que el modelo complejo. Intuitivamente podemos observar que el modelo complejo está influenciado por los puntos specíficos de los datos en el primer conjunto de datos; dado que la posición exacta de estos puntos de datos fue influida por ruido aleatorio, esto lleva al modelo complejo a ajustarse mal en el nuevo conjunto de datos. A este fenómeno lo llamamos sobreajuste (overfitting en inglés). Por ahora es importante que mantengamos en mente que nuestro modelo debe ajustarse bien, pero no demasiado bien. Como lo dijo alguna vez Albert Einstein (1933): “Difícilmente se puede negar que el fin supremo de toda teoría es hacer que los elementos básicos irreductibles sean lo más simples y pocos posibles sin tener que renunciar a la representación adecuada de un solo dato de experiencia.” Lo cual frecuentemente se parafrasea como: “Todo debe de ser tan simple como pueda ser, pero no más simple.”

5.5 Resumir datos usando la media

Ya nos hemos encontrado con la media (o promedio) más arriba, y de hecho, la mayoría de las personas conoce qué es un promedio, incluso aunque nunca haya tomado una clase de estadística. Es más comunmente usada para describir lo que llamamos la “tendencia central” del conjunto de datos – ¿cuál es el valor en el que se centran los datos? La mayoría de las personas no piensa que calcular una media es ajustar un modelo a los datos. Sin embargo, eso es exactamente lo que estamos haciendo cuando calculamos la media.

Ya hemos revisado la fórmula para calcular la media de una muestra de datos:

\[ \bar{X} = \frac{\sum_{i=1}^{n}x_i}{n} \]

Nota que dije que esta fórmula es específica para una muestra de datos, lo cual es un grupo de datos seleccionados de una población más grande. Usando una muestra, deseamos caracterizar una población más grande – el conjunto total de individuos en lxs que estamos interesadxs. Por ejemplo, si fuéramos unx encuestadxr político nuestra población de interés tal vez serían todxs lxs votantes registradxs, mientras que nuestra muestra podría incluir solo unos pocos miles de personas de esta población. En el capítulo 7 estaremos hablando con más detalle sobre el muestreo, pero por ahora el punto importante es que a lxs estadísticxs generalmente les gusta usar diferentes símbolos para diferenciar estadísticas que describen valores para una muestra, de parámetros que describen los valores verdaderos para una población; en este caso la fórmula para la media (denotada como \(\mu\)) de la población es:

\[ \mu = \frac{\sum_{i=1}^{N}x_i}{N} \]

donde N es el tamaño de la población completa.

Ya hemos visto que la media es el estimador que nos garantiza darnos un error promedio de cero, pero también aprendimos que el error promedio no es el mejor criterio; en su lugar, queremos un estimador que nos brinde la suma de errores cuadráticos (SSE, sum of squared errors) más baja, que también obtenemos usando la media. Podemos probar esto usando cálculo, pero en su lugar vamos a demostrarlo gráficamente en la Figura 5.7.

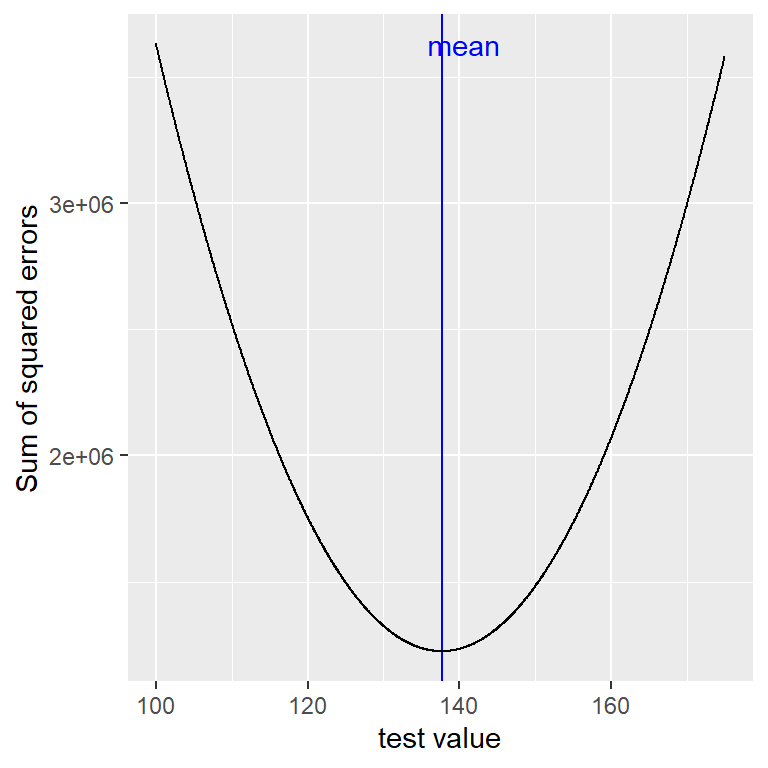
Figura 5.7: Una demostración de la media como la estadística que minimiza la suma de los errores cuadráticos. Utilizando los datos de la altura del NHANES, calculamos la media (la barra azul). Luego, probamos un rango de posibles estimaciones de parámetros, y por cada uno calculamos la suma de errores cuadráticos por cada dato de ese valor, el cual se indica por la curva negra. Vemos que la media cae al mínimo en la gráfica del error cuadrático.

El minimizar la suma de los errores cuadráticos (SSE) es una buena característica, y es la razón por la que la media es el estadístico más comúnmente usado para resumir datos. No obstante, la media también tiene su lado oscuro. Digamos que hay cinco personas en un bar, y examinamos el ingreso económico de cada unx (Tabla 5.1):

Tabla 5.1: Ingreso de nuestros cinco clientes en el bar.

income	person
48000	Joe
64000	Karen
58000	Mark
72000	Andrea
66000	Pat

La media (61600.00) parece ser una buena herramienta para medir el ingreso económico de esas cinco personas. Ahora observemos lo que pasa cuando Beyoncé Knowles entra al bar (Tabla 5.2):

Tabla 5.2: Ingreso de nuestros cinco clientes en el bar más Beyoncé Knowles.

income	person
48000	Joe
64000	Karen
58000	Mark
72000	Andrea
66000	Pat
54000000	Beyonce

La media es ahora casi 10 millones de dólares, lo cual no es verdaderamente representativo de lo que ganan las primeras cinco personas que estaban en el bar – en particular, la media está altamente influenciada por el valor extremo de Beyoncé. En general, la media es altamente sensible a valores extremos. Es por eso que siempre es importante asegurarnos de que no haya valores extremos cuando utilicemos la media para resumir datos.

5.6 Resumir datos robústamente usando la mediana

Si queremos resumir los datos en una forma que sea menos sensible a valores atípicos, podemos utilizar otra herramienta estadística llamada la mediana. Si acomodáramos todos los valores en orden de su magnitud, entonces la mediana es el valor que queda en medio. Si hay un número par de valores, entonces habrá dos valores empatados para el lugar medio, en cuyo caso tomamos la media (es decir, el punto medio) de esos dos números.

Veamos un ejemplo: Digamos que queremos resumir los siguientes valores:

8  6  3 14 12  7  6  4  9

Si ordenamos dichos valores:

3  4  6  6  7  8  9 12 14

Entonces la mediana es el valor de en medio – en este caso, el quinto de los nueve valores; es decir, el valor de la mediana sería igual a 7.

Mientras que la media minimiza la suma de los errores cuadráticos, la mediana minimiza una cantidad ligeramente distinta: la suma de los errores en valores absolutos (absolute value of errors). Esto explica por qué es menos sensible a valores atípicos – elevar al cuadrado va a exacerbar el efecto de errores grandes en comparación con tomar el valor absoluto. Podemos ver esto en el caso del ingreso económico: la mediana de ingreso ($65,000) es mucho más representativa de todo el grupo que la media ($9,051,333), y menos sensible al valor atípico tan grande.

Dado esto, ¿por qué utilizaríamos entonces la media? Como veremos más adelante en este capítulo, la media es el “mejor” estimador en el sentido de que varía menos de muestra en muestra en comparación con otros estimadores. Queda en nosotrxs decidir si vale la pena su sensibilidad a posibles valores atípicos – la estadística se trata de balancear ventajas y desventajas.

5.7 La moda

A veces deseamos describir la tendencia central de un conjunto de datos que no es numérico. Por ejemplo, digamos que queremos saber cuáles modelos de iPhones son más comunmente usados. Para probar esto, podemos preguntarle a un grupo grande de usuarios de iPhone cuál modelo es el que cada unx tiene. Si sacáramos el promedio de esos valores posiblemente veamos que la media del modelo de iPhone sería 9.51, lo cual no tiene sentido, ya que, el número de modelo de iPhone no están diseñados para ser mediciones cuantitativas. En este caso, una medición de tendencia central más apropiada es la moda, que sería el valor más común en el conjunto de datos.

5.8 Variabilidad: ¿Qué tan bien se ajusta la media a los datos?

Una vez que hemos descrito la tendencia central de los datos, a menudo también vamos a querer describir qué tan variables son los datos – a esto se le refiere también como “dispersión,” reflejando el hecho de que describe qué tan dispersos están los datos.

Ya hemos encontrado la suma de errores cuadráticos arriba, lo cual es la base para las mediciones más comunmente usadas para la variablidad: la varianza y la desviación estándar. La varianza para una población (referida como \(\sigma^2\)) es simplemente la suma de los errores cuadráticos divididos entre el número de observaciones– lo cual es exactamente lo mismo que el error cuadrático medio del que hablamos hace poco:

\[ \sigma^2 = \frac{SSE}{N} = \frac{\sum_{i=1}^n (x_i - \mu)^2}{N} \]

donde \(\mu\) es la media de la población. La desviación estándar es simplemente la raíz cuadrada de esto – es la raíz del error cuadrático medio que vimos antes. La desviación estándar es útil porque los errores están en las mismas unidades que en los datos originales (al deshacer el cuadrado que aplicamos a los errores).

Usualmente no tenemos acceso a toda la población, por lo que debemos calcular la varianza utilizando una muestra, a la cual nos referimos como \(\hat{\sigma}^2\), con el “sombrero” representando el hecho de que es un estimado basado en una muestra. La ecuación para \(\hat{\sigma}^2\) es similar a la de \(\sigma^2\):

\[ \hat{\sigma}^2 = \frac{\sum_{i=1}^n (x_i - \bar{X})^2}{n-1} \]

La única diferencia entre las dos ecuaciones es que dividimos entre \(n - 1\) en lugar de \(N\). Esto se relaciona con un concepto estadístico fundamental: grados de libertad. Recuerda que para calcular la varianza de la muestra, primero tuvimos que estimar la media de la muestra \(\bar{X}\). Al haber estimado esto, un valor en los datos ya no puede variar libremente. Por ejemplo, digamos que tenemos los siguientes datos para una variable \(x\): [3, 5, 7, 9, 11], la media es 7. Porque sabemos que la media de este conjunto de datos es 7, podemos calcular cuál sería cualquier valor específico si faltara. Por ejemplo, digamos que ocultamos el primer valor (3). Al hacer esto, aún sabemos que su valor debe de ser 3, porque la media de 7 implica que la suma de todos los valores es \(7 * n = 35\) y \(35 - (5 + 7 + 9 + 11) = 3\).

Entonces, cuando decimos que hemos “perdido” un grado de libertad, quiere decir que hay un valor que no puede variar libremente después de haberse acomodado al modelo. En el contexto de la varianza de la muestra, si no contemplamos la pérdida de grados de libertad, entonces nuestra estimación de la varianza de la muestra estará sesgada, ocasionando que subestimemos la incertidumbre de nuestra estimación de la media.

5.9 Usar simulaciones para entender la estadística

Soy un ávido creyente en el uso de simulaciones en computadora para comprender conceptos de estadística, y en capítulos futuros ahondaremos más en su uso. Aquí les presentaré la idea preguntándoles si podemos confirmar la necesidad de restar 1 del tamaño de la muestra al calcular la varianza de la muestra.

Usemos la muestra completa de los datos de lxs niñxs de NHANES como nuestra “población,” y observemos qué tan bien los cálculos de la varianza de la muestra utilizando tanto \(n\) como \(n-1\) en el denominador estimará la varianza de esta población a lo largo de un gran número de muestras simuladas aleatorias obtenidas del conjunto de datos. Regresaremos a los detalles de cómo se hace esto en un capítulo próximo.

Tabla 5.3: Variance estimates using n versus n-1; the estimate using n-1 is closer to the population value

Estimate	Value
Population variance	725
Variance estimate using n	710
Variance estimate using n-1	725

Los resultados de la Tabla 5.3 nos demuestran que la teoría propuesta arriba era correcta: la varianza estimada utilizando \(n - 1\) como el denominador se acerca mucho a la varianza calculada con todos los datos (la población), por lo que la varianza calculada utilizando \(n\) como el denominador está sesgada en comparación con el valor real.

5.10 Puntajes Z

Habiendo caracterizado una distribución en términos de su tendencia central y su variabilidad, a menudo es útil expresar los puntajes individuales en términos de en dónde se ubican con respecto a la distribución total. Digamos que estamos interesadxs en determinar si California es un lugar particularmente peligroso. Podemos responder a esta pregunta utilizando datos del 2014 del [FBI’s Uniform Crime Reporting Site] (https://www.ucrdatatool.gov/Search/Crime/State/RunCrimeOneYearofData.cfm). El panel de la izquierda de la Figura 5.8 muestra un histograma del número de crímenes violentos por estado, resaltando el valor de California. Observando estos datos, parece que California es terriblemente peligroso, con 153709 crímenes en ese año. Podemos visualizar estos datos al generar un mapa mostrando una distribución de la variable a lo largo de los estados, el cual se presenta en el panel de la derecha de la Figura 5.8.

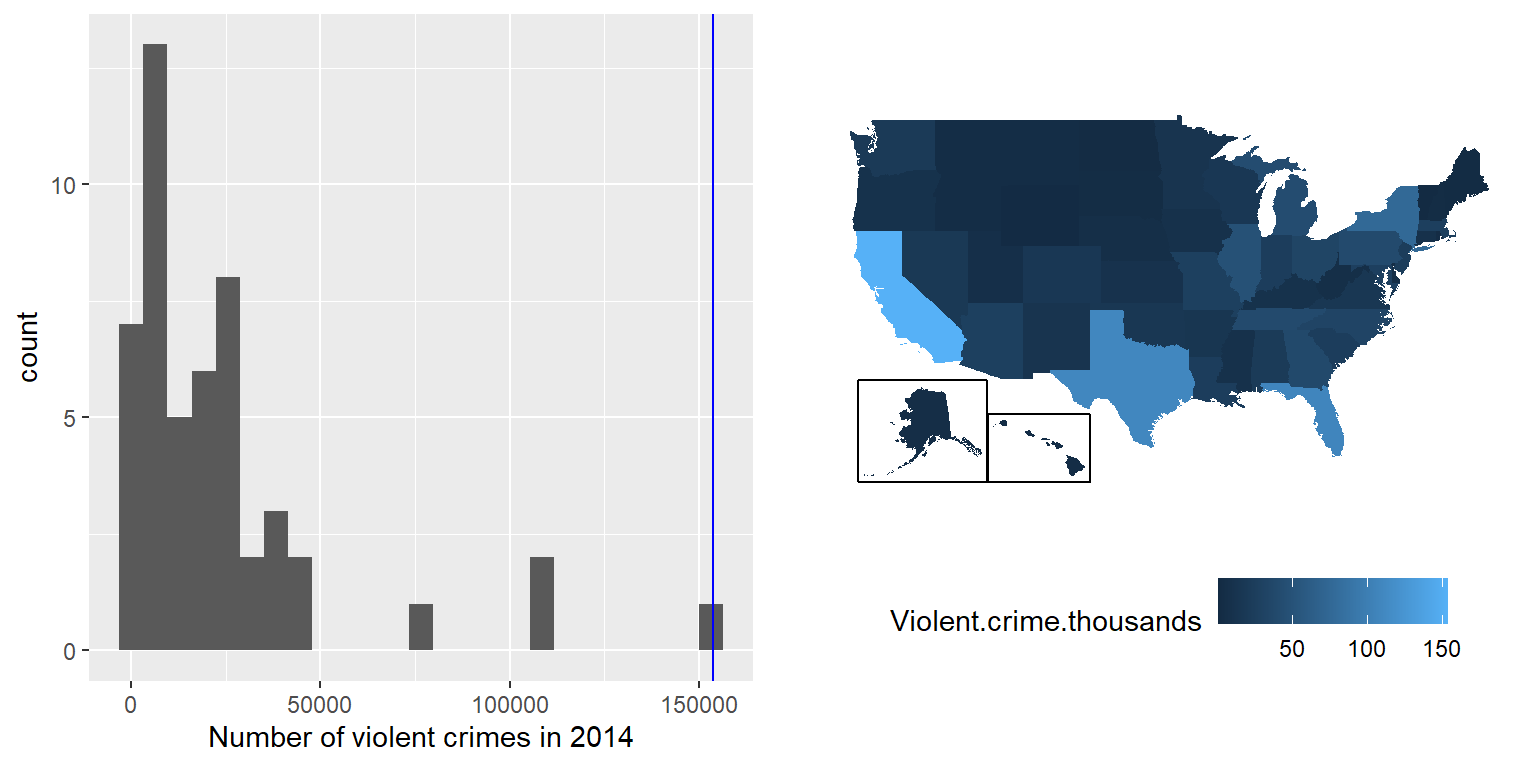
Figura 5.8: Izquierda: Histograma del número de crímenes violentos. El valor para CA está graficado en azul. Derecha: Un mapa de los mismos datos, con el número de crímenes (en miles) graficado para cada estado en color.

Tal vez hayas notado que California también tiene la población más grande de cualquier estado en Estados Unidos, por lo que es razonable que también tenga un gran número de crímenes. Si graficamos los números de crímenes junto con la población de cada estado (ve el panel izquierdo de la Figura 5.9), vemos que hay una relación directa entre las dos variables.

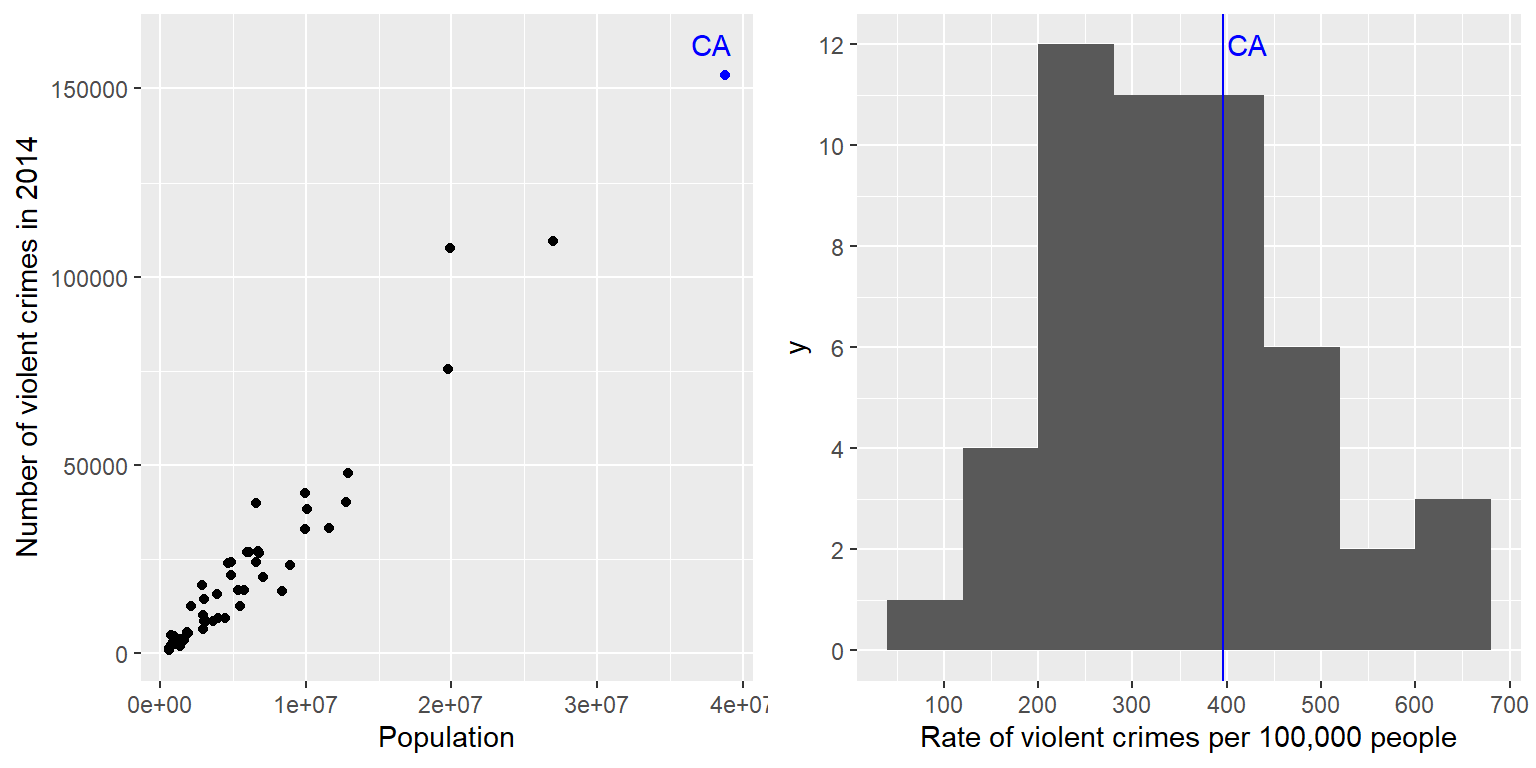
Figura 5.9: Izquierda: Una gráfica del número de crímenes violentos versus la población de cada estado. Derecha: Un histograma de la tasa de crímenes violentos per cápita, expresada en cantidad de crímenes por 100,000 habitantes.

En lugar de utilizar los números en bruto (o crudos) para los crímenes, debemos usar la tasa de crímenes violentos per cápita, el cual obtenemos al dividir el número de crímenes por estado entre la población de cada estado. El conjunto de datos del FBI ya incluye este valor (expresado como tasa por 100,000 habitantes). Observando el panel de la derecha de la Figura 5.9, podemos ver que California no es tan peligrosa después de todo – su tasa de crímenes de 396.10 por cada 100,000 habitantes está un poco por arriba de la media de los estados de 346.81, pero está dentro del rango de muchos otros estados. ¿Pero qué pasa si queremos obtener una vista más clara de qué tanto se aleja California del resto de la distribución?

El puntaje Z (Z-score) nos permite expresar datos en una forma que proporciona más información sobre cada punto de datos y su relación con el total de la distribución. La fórmula para calcular el puntaje Z para un dato invididual dado que ya conozcamos el valor de la media de la población \(\mu\) y su desviación estándar \(\sigma\) es:

\[ Z(x) = \frac{x - \mu}{\sigma} \]

Intuitivamente, podemos pensar en un puntaje Z como un indicador que nos dice qué tan lejos está cada punto o dato individual en referencia con la media, en unidades de la desviación estándar. Podemos calcular esto para los datos de la tasa de crímenes, como se muestra en la Figura 5.10, la cual grafica los puntajes Z contra los puntajes originales.

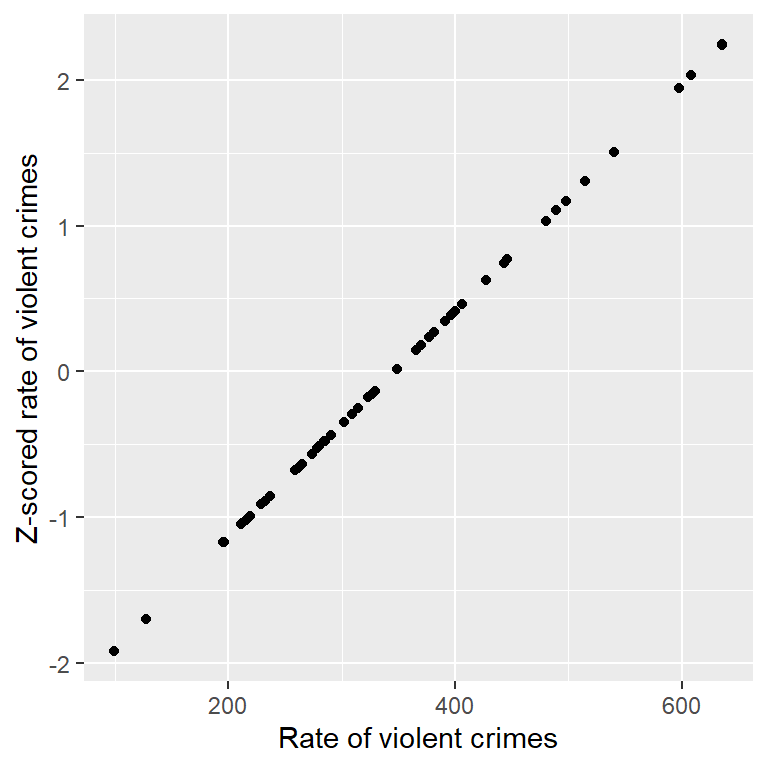
Figura 5.10: Gráfica de dispersión (scatterplot) de los datos originales de tasa de crímenes contra los datos en puntajes Z (Z-scores).

El diagrama de dispersión nos muestra que el proceso de sacar el puntaje Z no cambia la distribución relativa de los datos (esto es visible en el hecho de que los datos originales y el puntaje Z de los datos caen en una línea recta cuando se grafican una contra la otra). Sólo las acomoda para que tengan una media de cero y una desviación estándar de uno. En la figura 5.11 se muestran geográficamente los datos de crimen utilizando valores Z.

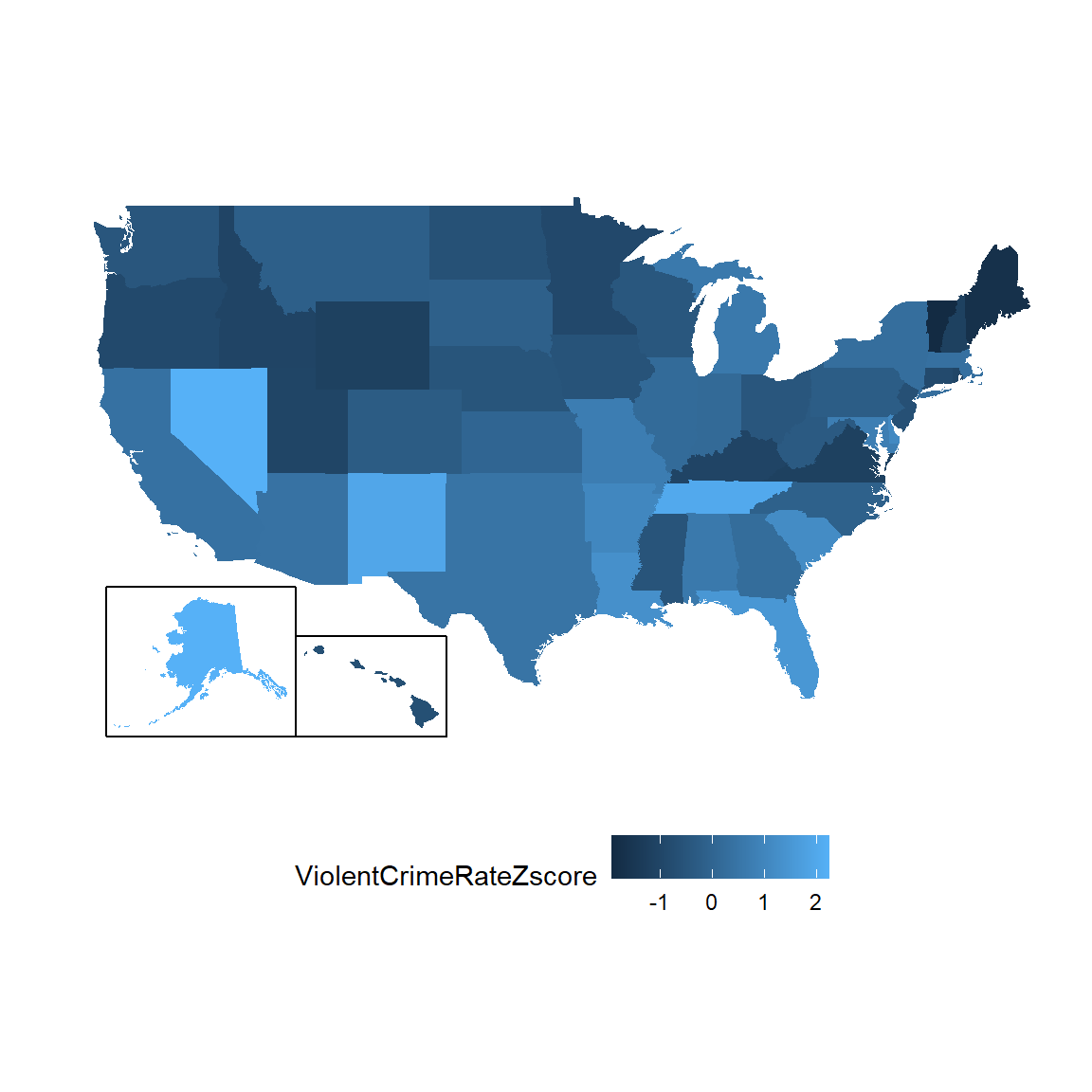
Figura 5.11: Datos de crímenes graficados sobre un mapa de Estados Unidos, presentados en puntajes Z (Z-scores).

Esto nos da una mirada un poco más interpretable de los datos. Por ejemplo, ahora podemos ver que Nevada, Tenessee y Nuevo México tienen tasas de crímenes que están aproximadamente dos desviaciones estándar por encima de la media.

5.10.1 Interpretando Puntajes Z

La “Z” en un “puntaje Z” proviene del hecho de que la distribución estándar normal (la distribución normal con una media de cero y una desviación estándar de 1) es a menudo referida como la distribución “Z.” Podemos usar la distribución estándar normal para ayudarnos a comprender lo que los puntajes Z específicos nos dicen acerca de dónde se encuentra un punto de datos con respecto al resto de la distribución.

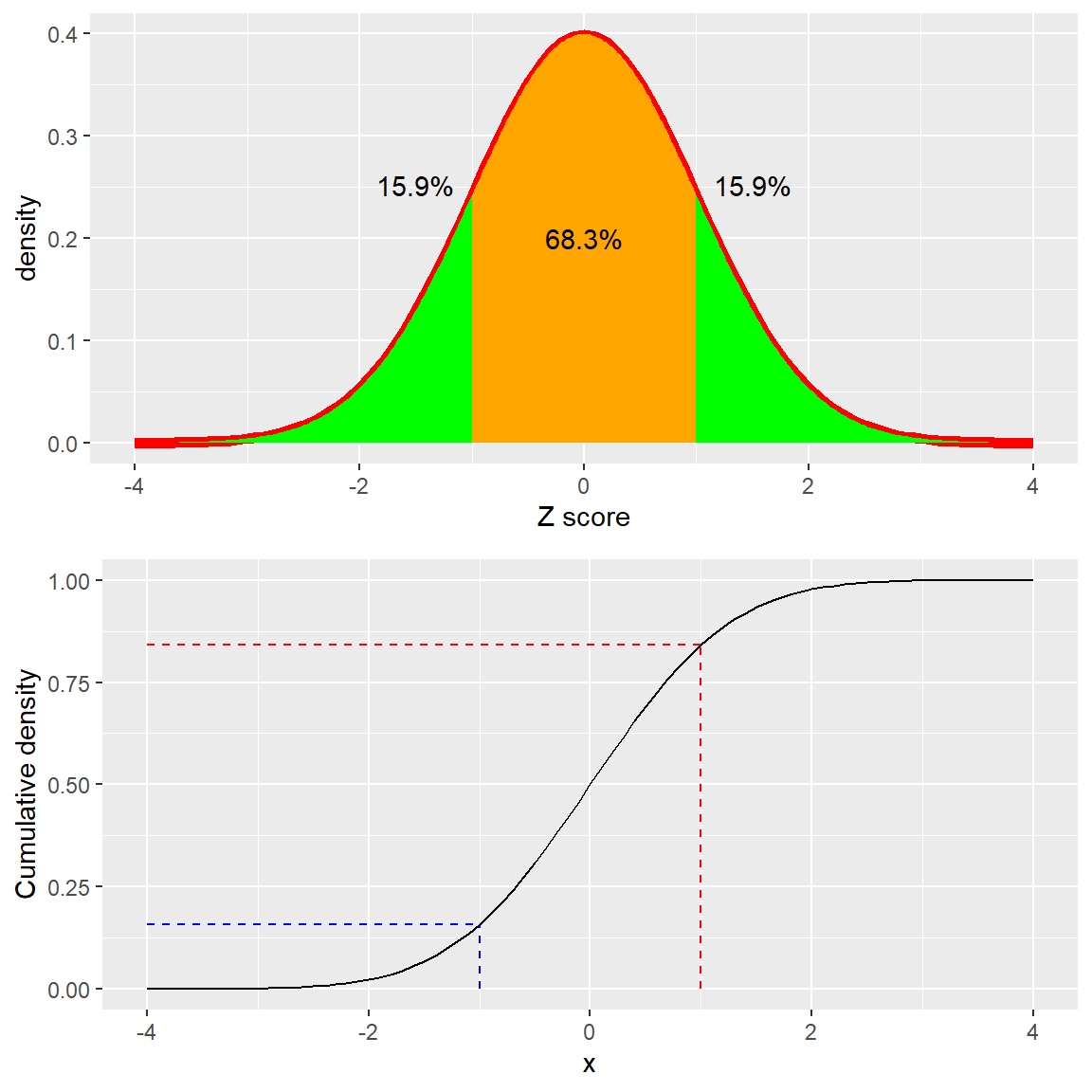
Figura 5.12: Distribución de densidad (arriba) y acumulada (abajo) de una distribución normal estándar, con puntos de corte (cutoffs) marcados a una desviación estándar arriba/abajo de la media.

El panel de arriba en la Figura 5.12 muestra que esperamos que el 16% de los valores caigan en \(Z\ge 1\), y que la misma proporción caiga en \(Z\le -1\).

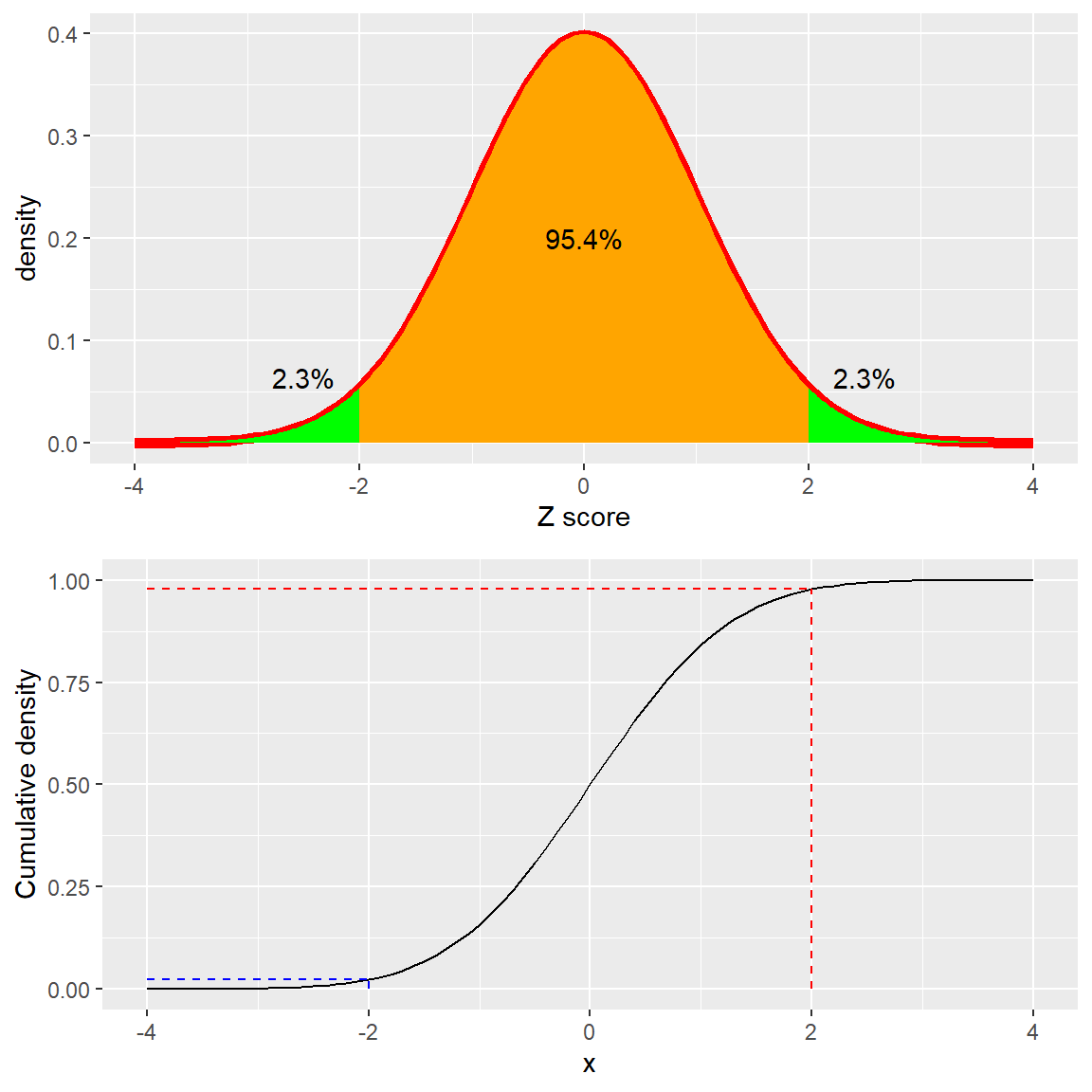
Figura 5.13: Distribución de densidad (arriba) y acumulada (abajo) de una distribución normal estándar, con puntos de corte (cutoffs) marcados a dos desviaciones estándar arriba/abajo de la media.

En la Figura 5.13 se muestra la misma gráfica para dos desviaciones estándar. Aquí podemos ver que solamente el 2.3% de los valores caen en \(Z \le -2\) y lo mismo en \(Z \ge 2\). Por lo que, si conocemos el puntaje Z para un punto en particular de los datos podemos estimar qué tan probable o improbable sería encontrar un valor al menos tan extremo como ese valor, lo que nos permite poner los valores en un mejor contexto. En el caso de las tasas de crímenes, vemos que California tiene un puntaje Z de 0.38 por su tasa de crímenes violentos per cápita, mostrando que está muy cerca de la media de otros estados, cerca del 35% de los estados tienen mayores tasas y 65% de los estados tienen menores tasas.

5.10.2 Puntajes Estandarizados

Digamos que en lugar de puntajes Z, queremos generar puntajes estandarizados de crimen con una media de 100 y una desviación estándar de 10. Esto es similar a la estandarización que se hace con puntajes de tests de inteligencia para generar un cociente intelectual (CI, en inglés IQ, Intelligence quotient). Podemos hacer esto al multiplicar los puntajes Z por 10 y luego sumar 100.

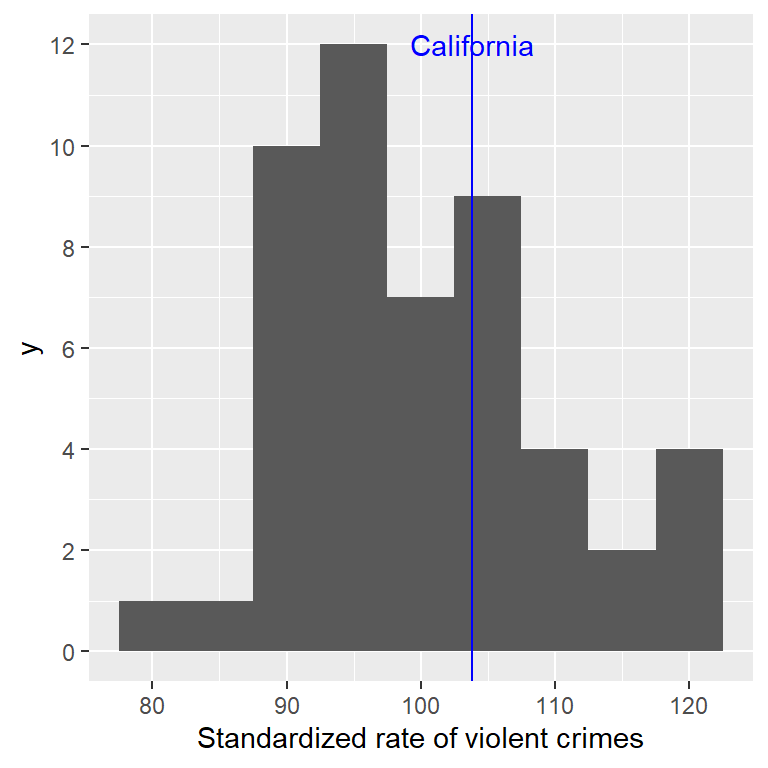
Figura 5.14: Datos de crímenes presentados como puntajes estandarizados con una media de 100 y una desviación estándar de 10.

5.10.2.1 Usar puntajes Z para comparar distribuciones

Un uso útil de los puntajes Z es para comparar distribuciones de diferentes variables. Digamos que queremos comparar las distribuciones de crímenes violentos y crímenes en propiedades privadas entre estados. En el panel de la izquierda de la Figura 5.15 graficamos ambos, uno contra el otro, con California representada en azul. Como puedes ver, las tasas brutas de delitos contra la propiedad son mucho más altos que las tasas brutas de crímenes violentos, por lo que no podemos solamente comparar los números directamente. Sin embargo, podemos graficar los puntajes Z para estos datos, uno contra otro (panel de la derecha de la Figura 5.15) – Aquí de nuevo podemos ver que la distribución de los datos no cambia. Al haber puesto los datos en puntajes Z para cada variable los hace comparables, y podemos ver ahora que California está justo en el medio de la distribución en términos de crímenes violentos y de crímenes de propiedad privada.

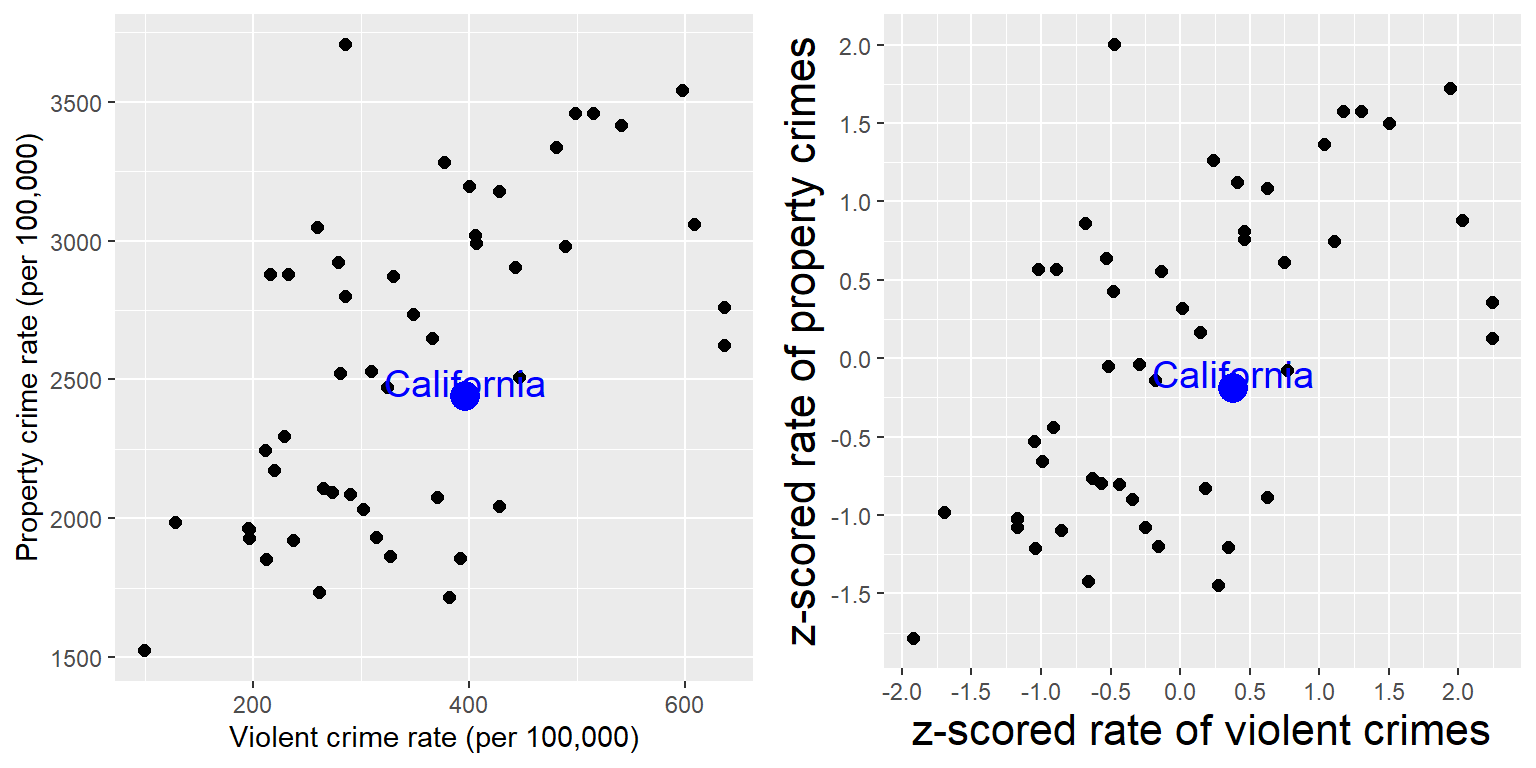
Figura 5.15: Gráfica de tasas de crímenes violentos vs. crímenes contra propiedad (izquierda) y tasas en puntajes Z (derecha).

Vamos a añadir otro factor a la gráfica: Población. En el panel izquierdo de la Figura 5.16, mostramos esto utilizando el tamaño del símbolo para graficar, el cual es comúnmente una forma útil de añadir información a la gráfica.

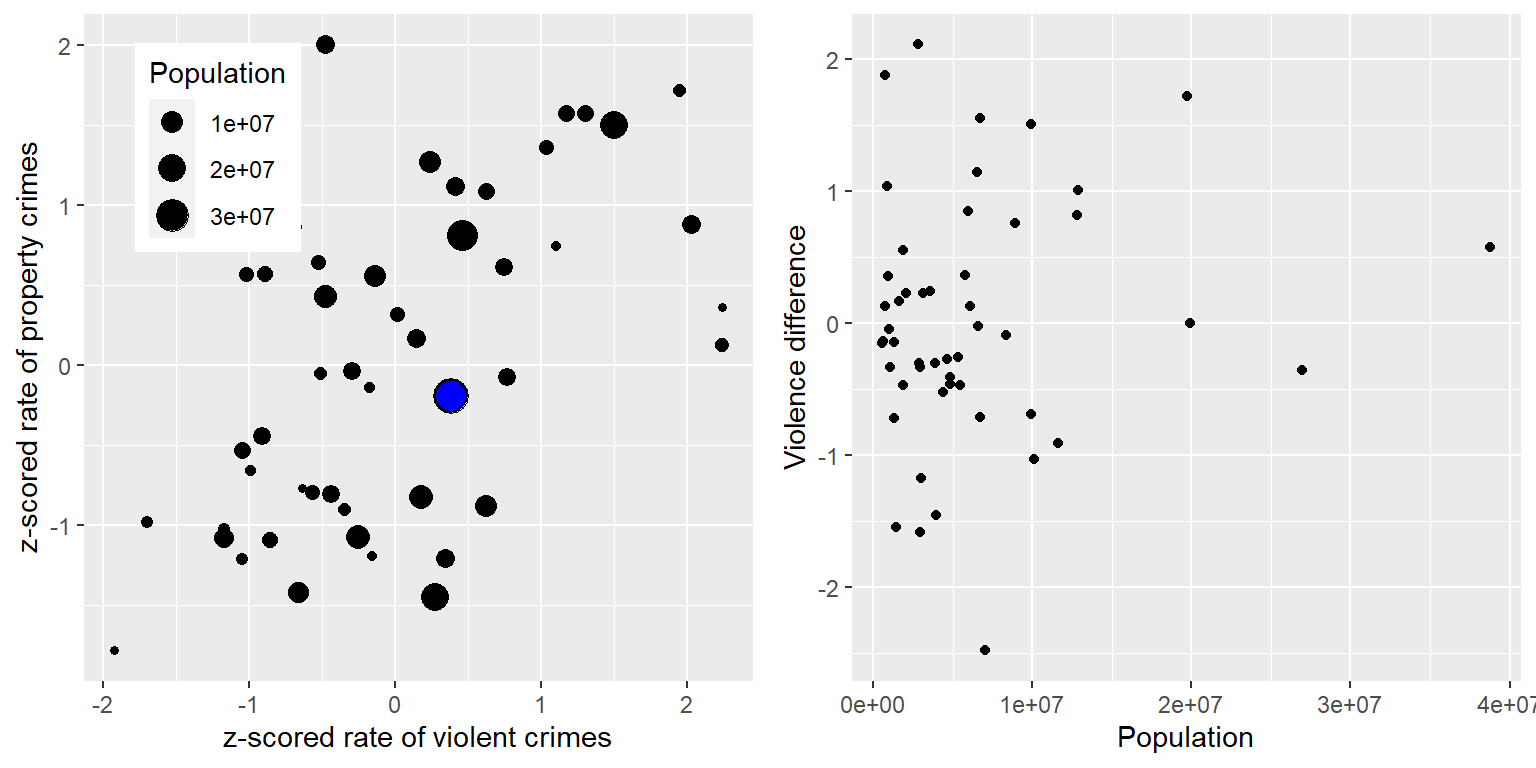
Figura 5.16: Izquierda: Gráfica de tasas de crímenes violentos vs. crímenes contra propiedad, con el tamaño de la población representado por el tamaño del símbolo graficado; California se presenta en azul. Derecha: Puntajes de la diferencia entre crímenes violentos vs. crímenes contra propiedad, graficados contra el tamaño de la población.

Porque los puntajes Z son directamente comparables, también podemos calcular puntuaciones diferenciales (difference scores) que expresan la tasa relativa de delitos violentos y no violentos (contra la propiedad) en cada estado. Luego podemos graficar esos puntajes en comparación con la población (mira el Panel derecho de la Figura 5.16). Esto muestra cómo podemos usar los puntajes Z para unir diferentes variables en una escala común.

Vale la pena mencionar que los estados más pequeños parecen tener la diferencia más grande en ambas direcciones. Si bien puede ser tentador observar cada estado e intentar determinar porqué tienen una puntuación de diferencia alta o baja, esto probablemente refleja el hecho de que las estimaciones obtenidas de muestras más pequeñas necesariamente serán más variables, como discutiremos en el capítulo 7.

5.11 Objetivos de aprendizaje

Al leer este capítulo deberás de ser capaz de:

• Describir ecuaciones básicas para modelos estadísticos (datos = modelo + error).
• Describir diferentes medidas de tendencia central y dispersión, cómo se calculan y cuáles son apropiadas bajo cuáles circunstancias.
• Calcular puntajes Z y describir por qué son útiles.

5.12 Apéndice

5.12.1 Prueba de que la suma de los errores a partir de la media es igual a cero

\[ error = \sum_{i=1}^{n}(x_i - \bar{X}) = 0 \]

\[ \sum_{i=1}^{n}x_i - \sum_{i=1}^{n}\bar{X}=0 \]

\[ \sum_{i=1}^{n}x_i = \sum_{i=1}^{n}\bar{X} \]

\[ \sum_{i=1}^{n}x_i = n\bar{X} \]

\[ \sum_{i=1}^{n}x_i = \sum_{i=1}^{n}x_i \]