Capitulo 2 Trabajar con Datos
2.1 ¿Qué son los datos?
Cuando hablamos de los datos lo hacemos en plural. Si te encuentras buscando información de estadística en inglés y aparece como “data,” recuerda que se trata de una palabra que siempre permanece en plural.
2.1.1 Datos Cualitativos
Los datos se componen de variables, en donde una variable refleja una medida o cantidad única. Algunas variables son cualitativas, lo que significa que describen una cualidad en lugar de una cantidad numérica. Por ejemplo, en mi curso de estadística generalmente doy un cuestionario introductorio, con el propósito de obtener datos que pueda usar en clase y para aprender más sobre los estudiantes. Una de las preguntas que hago es “¿Cuál es tu comida favorita?” a lo cual algunas de las respuestas han sido: arándanos, chocolate, tamales, pasta, pizza y mango. Esos datos no son esencialmente numéricos; podríamos asignarles números a cada uno (1=arándanos, 2=chocolate, etc), pero solamente estaríamos utilizando los números como etiquetas en lugar de números reales. Esto también restringe lo que podríamos hacer con esos números; por ejemplo, no tendría sentido el calcular el promedio de esos números. Sin embargo, a menudo codificaremos datos cualitativos utilizando números para poder trabajar más facilmente con ellos, como verán más adelante en este libro.
2.1.2 Datos cuantitativos
Más comunmente en estadística trabajaremos con datos cuantitativos, lo cual significa que los datos son numéricos. Por ejemplo, aquí en la Tabla 2.1 muestra los resultados de otra de las preguntas que realizo en mi clase introductoria, la cual es “¿Por qué estás tomando esta clase?”
| ¿Por qué estás tomando esta clase? | Número de estudiantes |
|---|---|
| Satisface un requisito de mi plan de estudios | 105 |
| Satisface un requisito de General Education Breadth | 32 |
| No es requisito, pero estoy interesadx en el tema | 11 |
| Otros | 4 |
Nota que las respuestas de lxs estudiantes fueron cualitativas, pero generamos un resumen cuantitativo contando cuántos estudiantes eligieron cada opción.
2.1.3 Tipos de números
Existen varios tipos diferentes de números con los que trabajamos en estadística. Es importante entender estas diferencias, en parte porque los lenguajes para análisis estadístico como R a menudo los distinguen.
Números binarios. Los más simples son los números binarios – cero ó uno. A menudo usaremos números binarios para representar si algo es verdadero o falso, o está presente o ausente. Por ejemplo, puede que le pregunte a 10 personas si alguna vez han tenido dolor de cabeza por migraña, registrando sus respuestas como “Sí” ó “No.” En ocasiones es útil usar valores lógicos, los cuales toman los valores de VERDADERO o FALSO. Esto puede ser especialmente útil cuando comenzamos a utilizar lenguajes de programación como R para analizar nuestros datos, ya que, estos lenguajes comprenden los conceptos de VERDADERO y FALSO. De hecho, la mayoría de los lenguajes de programación tratan los valores lógicos y los números binarios de manera equivalente. El número 1 es igual al valor lógico VERDADERO, y el número cero es igual al valor lógico FALSO.
Enteros. Los enteros son números enteros sin fracción o punto decimal. Nos encontramos más comunmente números enteros cuando contamos cosas, pero también ocurren en la medición de aspectos psicológicos. Por ejemplo, en mi cuestionario introductorio administro un set de preguntas sobre actitudes hacia la estadística (tal como “La estadística me parece misteriosa.”), para lo cual lxs estudiantes responden con un número entre 1 (“Totalmente en desacuerdo”) y 7 (“Totalmente de acuerdo”).
Números reales. En estadística trabajamos más comunmente con números reales, los cuales tienen parte fraccionaria o decimal. Por ejemplo, cuando medimos el peso de alguien, éste puede ser medido a un nivel arbitrario de precisión, desde kilogramos hasta microgramos.
2.2 Mediciones Discretas versus Continuas
Una medición discreta es aquella que toma uno de un conjunto finito de valores particulares. Estos pueden ser valores cualitativos (por ejemplo, diferentes tipos de razas de perros) o valores numéricos (por ejemplo, cuántos amigos tiene unx en Facebook). Es importante recordar que, no hay punto medio en las medidas; no tiene sentido decir que unx tiene 33.7 amigxs.
Una medición continua es aquella que es definida en términos de un número real. Puede encontrarse en cualquier parte de un rango particular de valores, aunque usualmente nuestras herramientas de medición pueden limitar la precisión con la que podemos medirla; por ejemplo, una báscula de piso puede medir el peso al kilogramo más cercano, aunque en teoría el peso puede ser medido con mucha mayor precisión.
En los cursos de estadística es común revisar con más detalle las diferentes “escalas” de medición, las cuales son discutidas con más detalle en el Apéndice de este capítulo. El punto más importante a recordar de esto es que algunos tipos de estadística no hacen sentido con algunos tipos de datos. Por ejemplo, imagina que reuniéramos el código postal de un grupo de individuos. Esos números son representados como enteros, pero en realidad no se refieren a una escala numérica; cada código postal sirve básicamente como etiqueta para una región diferente. Por esta razón, no tendría sentido hablar del código postal promedio.
2.3 ¿Qué constituye a una buena medición?
En muchas áreas, como en la psicología, aquello que estamos midiendo no es una característica física, sino más bien un concepto teórico inobservable, a lo cual usualmente nos referimos como un constructo. Por ejemplo, digamos que quiero probar qué tan bien entiendes la distinción entre los diferentes tipos de números descritos anteriormente. Te podría dar un examen sorpresa en donde te haría varias preguntas sobre estos conceptos y contaría cuántas respuestas tienes correctas. Esta prueba puede o puede no ser una buena medición del constructo de tu conocimiento real– por ejemplo, si escribiera una prueba en una forma confusa o un lenguaje que tú no entiendes, entonces la prueba puede sugerir que no entiendes los conceptos cuando en realidad sí los entiendes. Por otro lado, si te doy una prueba de opción múltiple con muchas respuestas obviamente incorrectas, entonces es posible que puedas desempeñarte bien en la prueba, incluso si en realidad no comprendes el material.
Usualmente es imposible medir un constructo sin cierto margen de error. En el ejemplo de arriba, puede que sepas la respuesta, pero puede que hayas leído mal la pregunta y por ende, obtenido una respuesta incorrecta. En otros casos, puede haber errores intrínsecos con respecto a aquella cosa que quiere ser medida, como cuando medimos cuánto le toma a una persona reaccionar en una simple prueba de tiempo de reacción, las cuales pueden variar de prueba en prueba por muchas razones. Generalmente queremos que nuestro error de medición sea lo más bajo posible, lo que podemos lograr mejorando la calidad de nuestras mediciones (por ejemplo, usando una mejor medición del tiempo para medir el tiempo de reacción), o promediando un mayor número de mediciones individuales.
A veces existe un estándar contra el que se pueden probar otras mediciones, al que podríamos referirnos como un “estándar dorado” (gold standard) – por ejemplo, la medición del sueño se puede realizar utilizando muchos dispositivos diferentes (como dispositivos que miden el movimiento de una persona mientras duerme), pero generalmente se consideran inferiores al estandar dorado de la polisomnografía (el cual es un examen que mide ondas cerebrales para cuantificar la cantidad de tiempo que una persona pasa en cada etapa del sueño). A menudo, el estándar dorado es más difícil o más caro de utilizar, y el método más barato es usado incluso cuando pueda tener un mayor margen de error.
Cuando pensamos en aquello que constituye a una buena medición, usualmente distinguimos dos diferentes aspectos que debe tener: debe de ser confiable, y debe de ser válida.
2.3.1 Confiabilidad
La confiabilidad se refiere a la consistencia de nuestras mediciones. Una forma común de confiabilidad, conocida como “confiabilidad test-retest,” mide qué tan bien concuerdan las mediciones si la misma medición se realiza dos veces. Por ejemplo, si te doy un cuestionario sobre tu actitud con respecto a la estadística hoy, y repito este mismo cuestionario mañana, al comparar tus respuestas en los dos días esperaríamos que tuvieran resultados muy similares entre sí, a menos que algo sucediera entre la aplicación de ambos cuestionarios que haya cambiado tu perspectiva de la estadística (¡como leer este libro!).
Otra forma de evaluar la confiabilidad surge en casos en que los datos incluyen juicios subjetivos. Por ejemplo, digamos que unx investigadorx quiere determinar si un tratamiento cambia qué tan bien interactúa unx niñx que se encuentra dentro del espectro autista con otros niñxs, lo cual es medido a través de expertos que observan al niñx y califican sus interacciones con lxs otrxs niñxs. En este caso queremos asegurarnos de que las respuestas no dependan del individuo que está calificando– nos gustaría que existiera una alta confiabilidad entre calificadores. Esto puede ser evaluado teniendo más de unx solx evaluadorx, y después al comparar sus calificaciones asegurarnos de que concuerden entre sí.
La confiabilidad es importante si queremos comparar una medición con otra, porque la relación entre dos variables diferentes no puede ser más fuerte que la relación entre cualquiera de las variables y ella misma (es decir, su confiabilidad). Esto significa que una medición no confiable nunca puede tener una relación estadísticamente fuerte con cualquier otra medición. Por esta razón, lxs investigadorxs que desarrollan una nueva medición (como un nuevo cuestionario) a menudo realizarán todo lo posible para establecer y mejorar su confiabilidad.
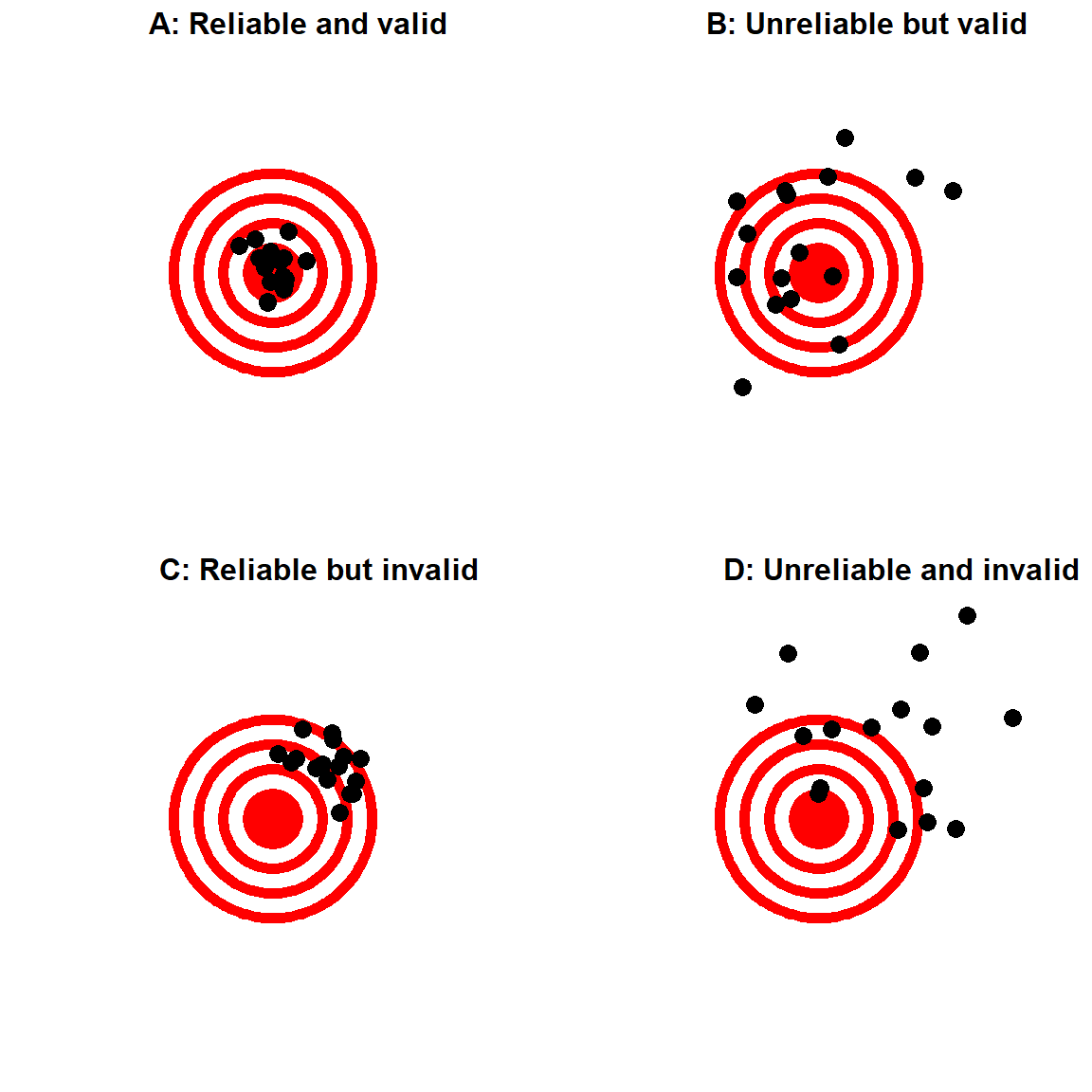
Figura 2.1: Una figura mostrando la diferencia entre confiabilidad y validez, usando tiros al blanco. Confiabilidad se refiere a la consistencia de la localización de los tiros, y validez se refiere a la precisión con que los tiros quedaron respecto al centro de las dianas.
2.3.2 Validez
La confiabilidad es importante, pero por sí misma no es suficiente: Después de todo, podríamos crear mediciones perfectamente confiables en una prueba de personalidad a través de re-codificar todas las respuestas utilizando el mismo número, sin importar qué haya respondido la persona. Queremos que nuestras mediciones sean también válidas– esto quiere decir que, nos queremos asegurar de que en realidad estemos midiendo el constructo que pensamos que estamos midiendo (Figura 2.1). Existen varios tipos diferentes de validez que son comúnmente discutidos; a continuación nos enfocaremos en tres de ellos.
Validez aparente. ¿La medición tiene sentido de forma aparente? Si te dijera que voy a medir la presión sanguínea de una persona con sólo observar el color de su lengua, probablemente pensarías que esta no es una medición válida aparente. Por otro lado, el utilizar un brazalete para medir la presión sanguínea tiene validez aparente. Esto es solamente un ejemplo simple antes de que nos centremos en aspectos más complejos de la validez.
Validez de constructo. Primero hay que preguntarnos, ¿esta medición se relaciona con otras mediciones de una forma apropiada? A menudo esto se subdivide en dos aspectos. Validez convergente quiere decir que la medición debería de estar estrechamente relacionada con otras mediciones que se supone reflejan el mismo constructo. Digamos que me interesa medir qué tan extrovertida es una persona mediante un cuestionario o una entrevista. La validez convergente se demostraría si estas dos medidas diferentes estuvieran estrechamente relacionadas entre sí. Por otro lado, las mediciones que se cree que reflejan diferentes constructos no deben estar relacionadas, lo que se conoce como validez divergente. Si mi teoría de la personalidad dice que la extraversión y la responsabilidad son dos constructos distintos, entonces también debería poder observar que mi medición de la extraversión no está relacionada con la medición de la responsabilidad.
Validez predictiva Si nuestras mediciones son verdaderamente válidas, entonces también deberían de poder predecir otros resultados. Por ejemplo, digamos que pensamos que el rasgo psicológico de la búsqueda de sensaciones (el deseo de nuevas experiencias) está relacionado con la toma de riesgos en el mundo real. Para probar la validez predictiva de una medición de la búsqueda de sensaciones, probaríamos qué tan bien los puntajes en la prueba predicen los puntajes en un cuestionario diferente que mide la toma de riesgos en el mundo real.
2.4 Objetivos de aprendizaje
Al haber leído este capítulo deberías de ser capaz de:
- Distinguir entre diferentes tipos de variables (cuantitativas/cualitativas, binarios/enteros/reales, discretos/continuos) y poder dar ejemplos de cada una de estas variables.
- Distinguir entre conceptos de confiabilidad y validez y poder aplicar cada concepto a un conjunto de datos en particular.
2.5 Lecturas sugeridas
- An Introduction to Psychometric Theory with Applications in R - Un libro de texto gratuito en línea sobre medición psicológica.
2.6 Apéndice
2.6.1 Escalas de medición
Todas las variables deben tomar al menos dos valores diferentes posibles (de lo contrario, serían una constante en lugar de una variable), pero diferentes valores de la variable pueden relacionarse entre sí de diferentes maneras, a lo cual nos referimos como escalas de medición. Hay cuatro formas en las que pueden diferir los diferentes valores de una variable.
- Identidad: Cada valor de la variable tiene un significado único.
- Magnitud: Los valores de la variable reflejan diferentes magnitudes y tienen una relación ordenada entre sí– por lo tanto, algunos valores son mayores y otros son menores.
- Intervalos iguales: Las unidades a lo largo de la escala de medición son iguales entre sí. Esto quiere decir, por ejemplo, que la diferencia entre 1 y 2 sería igual en su magnitud a la diferencia entre 19 y 20.
- Cero absoluto: La escala tiene un verdadero punto cero significativo. Por ejemplo, para muchas mediciones de cantidades físicas como la altura o el peso, este es la ausencia total de la cosa que está siendo medida.
Hay cuatro escalas diferentes de medición que van de la mano con estas diferentes formas en que los valores de una variable pueden diferir.
Escala Nominal. Una variable nominal satisface el criterio de identidad, de modo que cada valor de la variable representa algo diferente, pero los números simplemente sirven como etiquetas cualitativas, como mencionamos al principio. Por ejemplo, es posible que le preguntemos a las personas el partido politico al que se suscriben, y después codificar esa información como números: 1= “Republicanos,” 2= “Demócratas,” 3= “Libertarios,” etc. Sin embargo, los números no tienen ninguna relación ordenada entre sí.
Escala ordinal. Una variable ordinal satisface el criterio de identidad y magnitud, de manera que pueden ser ordenados en términos de su magnitud. Por ejemplo, le podemos preguntar a una persona con dolor crónico que llene un formato diario en donde evalúe qué tan mal siente su dolor, utilizando una escala numérica del 1 al 7. Hay que tomar en cuenta que, si bien la persona presumiblemente siente más dolor en un día en el que reporta un 6 frente a un día en que reporta un 3, no tendría sentido decir que su dolor es dos veces más intenso en el primero que en el segundo día; el orden nos da información sobre la magnitud relativa, pero las diferencias entre los valores no son necesariamente iguales en magnitud.
Escala de Intervalo. Una escala de intervalo tiene todas las características de una escala ordinal, pero además los intervalos entre unidades en la escala de medición pueden tratarse como iguales. Un ejemplo estándar es la temperatura física medida en grados Celsius o Fahrenheit; la diferencia física entre 10 y 20 grados es la misma que la diferencia física entre 90 y 100 grados, pero cada escala también puede tomar valores negativos.
Escala de proporción (o de razón). Una variable a escala de proporción/razón tiene las cuatro características que se describen anteriormente: Identidad, magnitud, intervalos iguales y cero absoluto. La diferencia entre una variable de escala de razón y una variable de escala de intervalo es que la variable de escala de razón tiene un verdadero punto cero. Ejemplos de variables de escala de razón incluyen la altura y el peso físicos, junto con la temperatura medida en Kelvin.
Hay dos razones importantes a las cuales les debemos de prestar atención a la escala de medición de la variable. En primer lugar, la escala determina qué tipo de operaciones matemáticas podemos aplicar a los datos (see Table 2.2). Una variable nominal solamente se puede comparar por igualdad; es decir, ¿dos observaciones de esa variable tienen el mismo valor numérico? No tendría sentido aplicar otras operaciones matemáticas a una variable nominal, ya que en realidad no funcionan como números en una variable nominal, sino más bien como etiquetas. Con las variables ordinales, también podemos probar si un valor es mayor o menor que otro, pero no podemos hacer ninguna aritmética. Las variables de intervalo y razón nos permiten realizar operaciones aritméticas; con variables de intervalo solo podemos sumar o restar valores, mientras que con variables de razón también podemos multiplicar y dividir valores.
| Igual/No igual | >/< | +/- | Multiplicar/dividir | |
|---|---|---|---|---|
| Nominal | OK | |||
| Ordinal | OK | OK | ||
| Intervalo | OK | OK | OK | |
| Razón | OK | OK | OK | OK |
Estas restricciones también implican que existen ciertos tipos de estadística que podemos calcular sobre cada tipo de variable. La estadística que solamente se trate de contar los diferentes valores (como el valor más común comunido como modo/moda), puede ser calculado en cualquiera de los tipos de variables. Otro tipo de estadística está basada en ordenar o en clasificar los valores (como la mediana, la cual es el valor que está en medio cuando todos los valores son ordenados por su magnitud), y estos requieren que el valor al menos esté en una escala ordinal. Finalmente, la estadística que se encarga de sumar los valores (como el promedio o media), requiere que las variables sean al menos en una escala de intervalo. Habiendo dicho esto, debemos tomar en cuenta que es común que lxs investigadorxs calculen la media de variables que son solo ordinales (como las respuestas en las pruebas de personalidad), pero esto a veces puede ser problemático.