Capitulo 15 Comparar medias

Hemos encontrado ya un número de casos donde queremos hacer preguntas acerca de la media de una muestra. En este capítulo, profundizaremos en las varias maneras en que podemos comparar medias entre grupos.

15.1 Probar el valor de una media simple

La pregunta más sencilla que podríamos hacernos acerca de una media es si tiene un valor específico. Digamos que queremos probar si el valor medio de presión sanguínea diastólica en adultos de la base de datos NHANES es mayor a 80, que es un punto de corte para hipertensión de acuerdo al Colegio Americano de Cardiología. Tomamos una muestra de 200 adultos para hacernos esta pregunta; cada adulto tiene su presión sanguínea medida en tres momentos, y usaremos el promedio de estos valores para nuestra prueba.

Una manera sencilla de probar esta diferencia es usando una prueba llamada prueba de los signos (sign test), que pregunta si la proporción de diferencias positivas entre el valor real y el valor hipotetizado es diferente que el que se esperaría por azar. Para hacer esto, tomamos las diferencias entre cada dato y el valor de la media hipotetizada y calculamos su signo. Si los datos están normalmente distribuidos y la media real es igual a la media hipotetizada, entonces la proporción de valores arriba de la media hipotetizada (o por debajo) debería ser 0.5, de tal manera que la proporción de diferencias positivas también debería ser de 0.5. En nuestra muestra, vemos que el 19.0 por ciento de las personas tienen una presión sanguínea diastólica arriba de 80. Luego podemos usar una prueba binomial para preguntarnos si la proporción de diferencias positivas es mayor a 0.5, usando la función de la prueba binomial en nuestro software estadístico:

## 
##  Exact binomial test
## 
## data:  npos and nrow(NHANES_sample)
## number of successes = 38, number of trials = 200, p-value = 1
## alternative hypothesis: true probability of success is greater than 0.5
## 95 percent confidence interval:
##  0.15 1.00
## sample estimates:
## probability of success 
##                   0.19

Aquí vemos que la proporción de personas con signo positivo no es muy sorprendente bajo la hipótesis nula de \(p \le 0.5\), lo que no debería sorprendernos dado que el valor observado en realidad es menor que \(0.5\).

También podemos hacer esta pregunta usando la prueba t de Student, que ya te has encontrado antes en este libro. Nos referiremos a la media como \(\bar{X}\) y a la media poblacional hipotetizada como \(\mu\). Entonces, la prueba t para una sola media es:

\[ t = \frac{\bar{X} - \mu}{SEM} \] donde SEM (standard error of the mean, o error estándar de la media, como podrás recordar del capítulo sobre muestreo) es definido por:

\[ SEM = \frac{\hat{\sigma}}{\sqrt{n}} \]

En esencia, el estadístico t pregunta qué tan grande es la desviación de la media muestral de la cantidad hipotetizada con respecto a la variabilidad muestral de la media.

Podemos calcular esto para la base de datos NHANES en nuestro software estadístico:

## 
##  One Sample t-test
## 
## data:  NHANES_adult$BPDiaAve
## t = -55, df = 4593, p-value = 1
## alternative hypothesis: true mean is greater than 80
## 95 percent confidence interval:
##   69 Inf
## sample estimates:
## mean of x 
##        70

Esto nos muestra que la media de presión sanguínea diastólica en la base de datos (69.5) es realmente mucho menor que 80, por lo que nuestra prueba sobre si la media es superior a 80 está muy lejos de resultar significativa.

Recuerda que un valor p grande no nos provee de evidencia en favor de la hipótesis nula, porque hemos asumido desde el inicio que la hipótesis nula es verdadera. Sin embargo, como discutimos en el capítulo sobre análisis Bayesiano, podemos usar el factor de Bayes para cuantificar la evidencia a favor o en contra de la hipótesis nula:

ttestBF(NHANES_sample$BPDiaAve, mu=80, nullInterval=c(-Inf, 80))
## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 -Inf<d<80    : 2.7e+16  ±NA%
## [2] Alt., r=0.707 !(-Inf<d<80) : NaNe-Inf ±NA%
## 
## Against denominator:
##   Null, mu = 80 
## ---
## Bayes factor type: BFoneSample, JZS

El primer factor de Bayes enlistado aquí (\(2.73 * 10^{16}\)) denota el hecho de que hay una evidencia excesivamente fuerte en favor de la hipóteis nula sobre la alternativa.

15.2 Comparar dos medias

Una pregunta más común que frecuentemente surge en estadística es si existe una diferencia entre las medias de dos grupos diferentes. Digamos que quisiéramos saber si fumadores regulares de marihuana miran más televisión, que también podemos preguntarnos usando la base de datos NHANES. Tomamos una muestra de 200 personas de la base de datos y probamos si el número de horas de ver televisión por día está relacionado con el uso regular de marihuana. El panel izquierdo de la Figura 15.1 muestra estos datos usando una gráfica de violín.

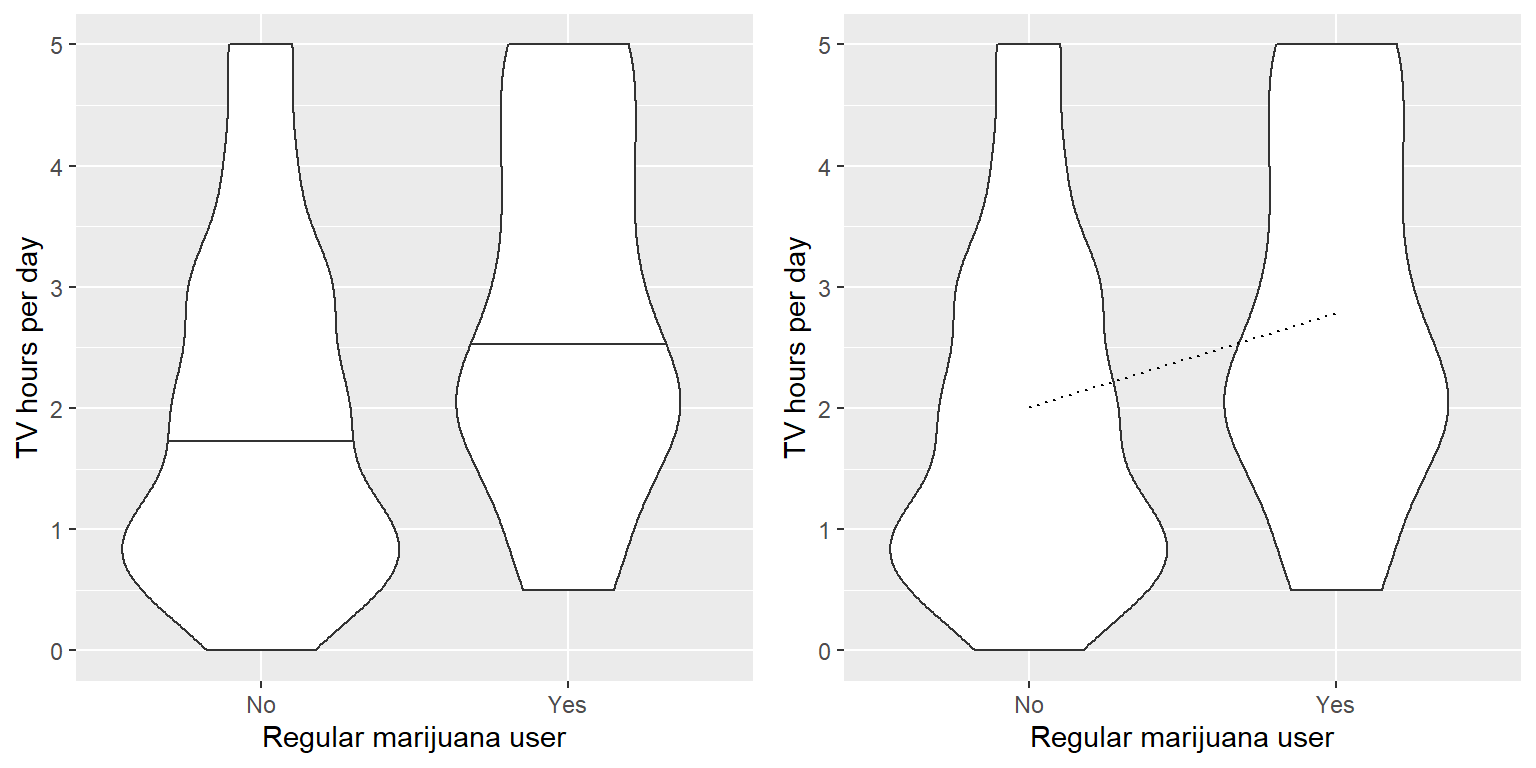
Izquierda: Gráfica de violín mostrando distribuciones de horas de ver TV por día separados por el uso regular de marihuana. Derecha: Gráficas de violín mostrando los datos para cada grupo, con una línea punteada conectando los valores predichos para cada grupo, calculado con base en los resultados del modelo lineal.

Figura 15.1: Izquierda: Gráfica de violín mostrando distribuciones de horas de ver TV por día separados por el uso regular de marihuana. Derecha: Gráficas de violín mostrando los datos para cada grupo, con una línea punteada conectando los valores predichos para cada grupo, calculado con base en los resultados del modelo lineal.

También podemos usar la prueba t de Student para probar diferencias entre dos grupos de observaciones independientes (como revisamos en un capítulo anterior); regresaremos después en este capítulo a casos donde las observaciones no son independientes. Como recordatorio, el estadístico t para comparaciones entre dos grupos independientes se calcula así:

\[ t = \frac{\bar{X_1} - \bar{X_2}}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}} \]

donde \(\bar{X}_1\) y \(\bar{X}_2\) son las medias de los dos grupos, \(S^2_1\) y \(S^2_2\) son las varianzas para cada grupo, y \(n_1\) y \(n_2\) son los tamaños de los dos grupos. Bajo la hipótesis nula de no diferencia entre medias, este estadístico se distribuye de acuerdo a una distribución t, con grados de libertad calculados usando la prueba de Welch (como se discutió previamente) puesto que el número de personas difiere entre los dos grupos. En este caso, comenzamos con la hipótesis específica de que fumar marihuana está asociado con mayor tiempo de ver TV, por lo que usaremos una prueba de una cola. Aquí están los resultados de nuestro software estadístico:

## 
##  Welch Two Sample t-test
## 
## data:  TVHrsNum by RegularMarij
## t = -3, df = 85, p-value = 6e-04
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##   -Inf -0.39
## sample estimates:
##  mean in group No mean in group Yes 
##               2.0               2.8

En este caso vemos que existe una diferencia estadísticamente significativa entre los grupos, en la dirección esperada - los fumadores regulares de marihuana ven más TV.

15.3 La prueba t como un modelo lineal

La prueba t es frecuentemente presentada como una herramienta especializada para comparar medias, pero también se puede ver como una aplicación del modelo lineal general. En este caso, el modelo se vería como esto:

\[ \hat{TV} = \hat{\beta_1}*Marihuana + \hat{\beta_0} \] Como el fumar es una variable binaria, la tratamos como una variable ficticia (dummy variable) como discutimos en el capítulo anterior, fijándola en un valor de 1 para fumadores o de cero para no fumadores. En este caso, \(\hat{\beta_1}\) es simplemente la diferencia de las medias entre los dos grupos, y \(\hat{\beta_0}\) es la media para el grupo que fue codificado con cero. Podemos ajustar este modelo usando la función del modelo lineal general en nuestro software estadístico, y ver que nos da el mismo estadístico t como la prueba t de arriba, excepto que fue positiva en este caso por la manera en que nuestro software ordena los grupos:

## 
## Call:
## lm(formula = TVHrsNum ~ RegularMarij, data = NHANES_sample)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.2843 -1.0067 -0.0067  0.9933  2.9933 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)        2.007      0.116   17.27  < 2e-16 ***
## RegularMarijYes    0.778      0.230    3.38  0.00087 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.4 on 198 degrees of freedom
## Multiple R-squared:  0.0546, Adjusted R-squared:  0.0498 
## F-statistic: 11.4 on 1 and 198 DF,  p-value: 0.000872

También podemos ver los resultados del model lineal gráficamente (ve el panel derecho de la Figura 15.1). En este caso, el valor predicho para no fumadores es \(\hat{\beta_0}\) (2.0), y el valor predicho para fumadores es \(\hat{\beta_0} +\hat{\beta_1}\) (2.8).

Para calcular los errores estándar para este análisis, podemos usar exactamente las mismas ecuaciones que usamos para regresión lineal – porque este es realmente sólo otro ejemplo de regresión lineal. De hecho, si comparas el valor p de la prueba t de arriba con el valor p en el análisis de regresión lineal para la variable de uso de marihuana, verás que el del análisis de regresión lineal es exactamente el doble que el de la prueba t, porque el análisis de regresión lineal está realizando una prueba de dos colas.

15.3.1 Tamaños de efecto para comparar dos medias

El tamaño de efecto más comúnmente usado para comparar dos medias es la d de Cohen, la cual (como recordarás del Capítulo 10) es una expresión del tamaño del efecto en términos de unidades de desviación estándar. Para la prueba t estimada usando el modelo lineal general desarrollado arriba (i.e. con una sola variable dummy codificada), esto es expresado como:

\[ d = \frac{\hat{\beta_1}}{\sigma_{residual}} \] Podemos obtener estos valores de la salida del análisis arriba, dándonos una d = 0.55, que generalmente interpretaríamos como un tamaño de efecto medio.

También podemos calcular \(R^2\) para este análisis, que nos dice qué proporción de la varianza en el tiempo de ver TV es explicada por el fumar marihuana. Este valor (que es reportado hasta abajo del resumen del análisis del modelo lineal) es 0.05, que nos dice que mientras que el efecto podrá ser estadísticamente significativo, explica relativamente poco de la varianza en tiempo de ver TV.

15.4 Factores de Bayes para diferencias entre medias

Como discutimos en el capítulo sobre análisis Bayesiano, los factores de Bayes nos proveen de una mejor manera de cuantificar la evidencia a favor o en contra de la hipótesis nula de no diferencia. Podemos calcular este análisis con los mismos datos:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf    : 0.041 ±0%
## [2] Alt., r=0.707 !(0<d<Inf) : 61    ±0%
## 
## Against denominator:
##   Null, mu1-mu2 = 0 
## ---
## Bayes factor type: BFindepSample, JZS

Por la manera en que los datos están organizados, la segunda línea nos muestra el factor de Bayes relevante para este análisis, que es 61.4. Esto nos muestra que la evidencia en contra de la hipótesis nula es bastante fuerte.

15.5 Comparar observaciones pareadas/relacionadas

En investigación experimental, frecuentemente usamos diseños intra-sujetos (within-subjects), en donde comparamos a la misma persona en múltiples mediciones. Las mediciones que se obtienen de este tipo de diseño son frecuentemente referidas como medidas repetidas (repeated measures). Por ejemplo, en la base de datos NHANES la presión sanguínea fue medida tres veces. Digamos que estamos interesados en probar si existe una diferencia en la presión sanguínea sistólica entre la primera y la segunda medición en las personas de nuestra muestra (Figura 15.2).

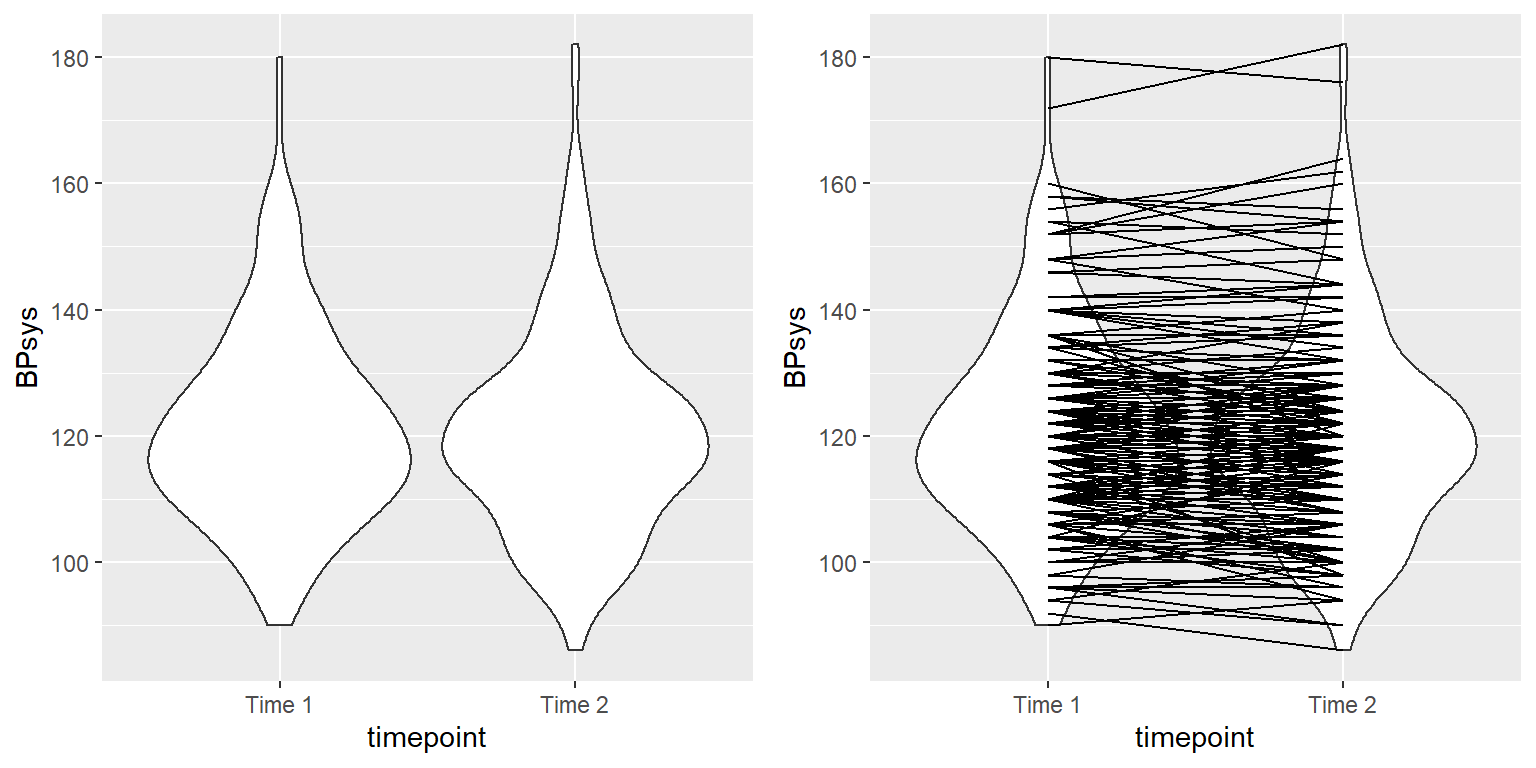
Izquierda: Gráfica de violín de la presión sanguínea sistólica en el primer y segundo registro, de NHANES. Derecha: Misma gráfica de violín con líneas conectando los dos registros de una misma persona.

Figura 15.2: Izquierda: Gráfica de violín de la presión sanguínea sistólica en el primer y segundo registro, de NHANES. Derecha: Misma gráfica de violín con líneas conectando los dos registros de una misma persona.

Vemos que no parece haber mucha diferencia en la media de presión sanguínea (cerca de un punto) entre la primera y la segunda medición. Primero probemos si hay una diferencia usando un prueba t para muestras independientes, la cual ignora el hecho que los pares de datos vienen de una misma persona.

## 
##  Two Sample t-test
## 
## data:  BPsys by timepoint
## t = 0.6, df = 398, p-value = 0.5
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.1  4.1
## sample estimates:
## mean in group BPSys1 mean in group BPSys2 
##                  121                  120

Este análisis muestra que no hay una diferencia estadísticamente significativa. Sin embargo, este análisis es inapropiado porque asume que las dos muestras son independientes, cuando de hecho no lo son, ya que los datos vienen de las mismas personas. Podemos graficar los datos con una línea para cada individuo para mostrar esto (ve el panel derecho de la Figura 15.2).

En este análisis, lo que realmente nos importa es saber si la presión sanguínea de cada persona cambia de una manera sistemática entre las dos mediciones, así que otra manera de representar estos datos es calculando la diferencia entre dos puntos en el tiempo para cada persona, y luego analizar estas diferencias en lugar de analizar las mediciones individuales. En la Figura 15.3 vemos un histograma de estas puntuaciones de diferencias, con una línea azul denotando la media de las diferencias.

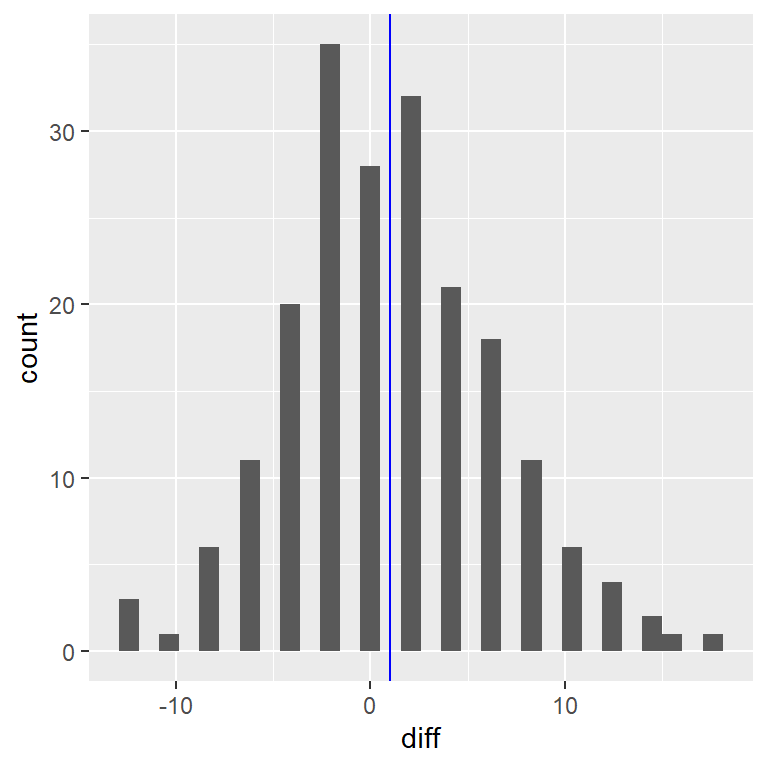
Histograma de las puntuaciones de diferencias entre la primera y la segunda medición de presión sanguínea. La línea vertical representa la diferencia promedio en la muestra.

Figura 15.3: Histograma de las puntuaciones de diferencias entre la primera y la segunda medición de presión sanguínea. La línea vertical representa la diferencia promedio en la muestra.

15.5.1 Prueba de los signos

Una manera simple de probar las diferencias es usando la prueba de los signos (sign test). Para hacer esto, tomamos las diferencias y calculamos su signo, y luego usamos la prueba binomial para preguntarnos si la proporción de signos positivos difiere de 0.5.

## 
##  Exact binomial test
## 
## data:  npos and nrow(NHANES_sample)
## number of successes = 96, number of trials = 200, p-value = 0.6
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.41 0.55
## sample estimates:
## probability of success 
##                   0.48

Aquí vemos que la proporción de personas con signos positivos (0.48) no es suficientemente grande como para ser sorprendente bajo la hipótesis nula de \(p=0.5\). Sin embargo, un problema con la prueba de los signos es que está descartando información acerca de la magnitud de las diferencias, y por lo tanto podría estar perdiéndose de algo.

15.5.2 Prueba t para muestras relacionadas (paired t-test)

Una estrategia más común es usar una prueba t para muestras relacionadas (paired t-test), que es el equivalente a una prueba t para una muestra en la cual se espera que la media de la diferencias entre mediciones para cada persona sea cero. Podemos calcular esto usando nuestro software estadístico, diciéndole que los datos son pareados/relacionados:

## 
##  Paired t-test
## 
## data:  BPsys by timepoint
## t = 3, df = 199, p-value = 0.007
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.29 1.75
## sample estimates:
## mean of the differences 
##                       1

Con este análisis vemos que de hecho existe una diferencia significativa entre las dos mediciones. Calculemos el factor de Bayes para ver cuánta evidencia brinda este resultado:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 : 3 ±0.01%
## 
## Against denominator:
##   Null, mu = 0 
## ---
## Bayes factor type: BFoneSample, JZS

El factor de Bayes observado de 2.97 nos dice que aunque el efecto fue significativo en la prueba t para muestras relacionadas, realmente provee de evidencia muy débil en favor de la hipótesis alternativa.

La prueba t para muestras relacionadas puede también ser definida en términos de un modelo lineal; ve el Apéndice para más detalles sobre esto.

15.6 Comparar más de dos medias

Frecuentemente queremos comparar más de dos medias para determinar si alguna de ellas difiere de las otras. Digamos que estamos analizando datos de un ensayo clínico sobre el tratamiento para presión sanguínea alta. En este estudio, los voluntarios se asignan aleatoriamente a una de tres posibles condiciones: Medicamento 1, Medicamento 2, o placebo. Generemos algunos datos y grafiquémoslos (ve la Figura 15.4).

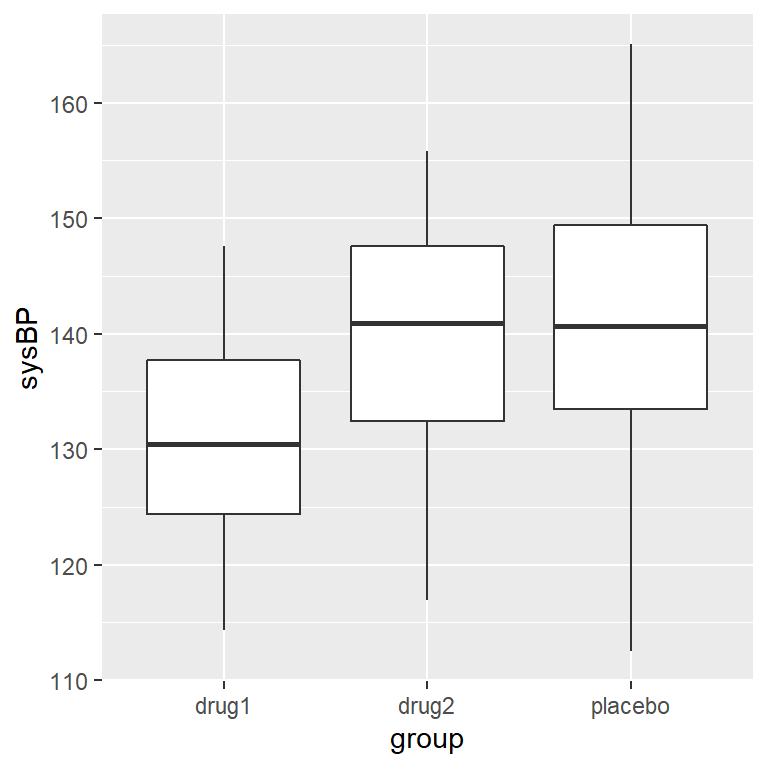
Boxplots mostrando la presión sanguínea de tres grupos diferentes en nuestro ensayo clínico.

Figura 15.4: Boxplots mostrando la presión sanguínea de tres grupos diferentes en nuestro ensayo clínico.

15.6.1 Análisis de varianza (analysis of variance, ANOVA)

Primero querríamos probar la hipótesis nula de que las medias de todos los grupos son iguales – esto es, que ninguno de los tratamientos tenga ningún efecto comparado con el placebo. Podemos hacer esto usando un método llamado análisis de varianza (analysis of variance, ANOVA). Este es uno de los métodos más comúnmente usados en estadística en psicología, aquí sólo lo revisaremos superficialmente. La idea básica detrás de ANOVA es una que ya discutimos en el capítulo sobre el modelo lineal general, y de hecho el ANOVA es sólo un nombre para una versión específica de ese modelo.

Recordarás del capítulo anterior que podemos dividir la varianza total de los datos (\(SS_{total}\), donde \(SS\) es por sum of squares) en la varianza que es explicada por el modelo (\(SS_{modelo}\)) y la varianza que no es explicada por el modelo (\(SS_{error}\)). Entonces podemos calcular la media cuadrática (mean square, \(MS\)) para cada una de éstas al dividirlas entre sus grados de libertad; para el error, los grados de libertad son \(N - p\) (donde \(p\) es el número de medias que calculamos), y para el modelo, son \(p - 1\):

\[ MS_{modelo} =\frac{SS_{modelo}}{df_{modelo}}= \frac{SS_{modelo}}{p-1} \]

\[ MS_{error} = \frac{SS_{error}}{df_{error}} = \frac{SS_{error}}{N - p} \]

Con ANOVA, queremos probar si la varianza explicada por el modelo es mayor que lo que esperaríamos por el azar, bajo la hipótesis nula de no diferencias entre medias. Mientras que para la distribución t el valor esperado es cero bajo la hipótesis nula, ese no es el caso aquí, porque las sumas de cuadrados dan siempre números positivos. Afortunadamente, existe otra distribución teórica que describe cómo las razones de sumas de cuadrados se distribuyen bajo la hipótesis nula: la distribución F (ve la Figura 15.5). Esta distribución considera dos diferentes grados de libertad, que corresponden a los grados de libertad del numerador (que en este caso es el modelo), y del denominador (que en este caso es el error).

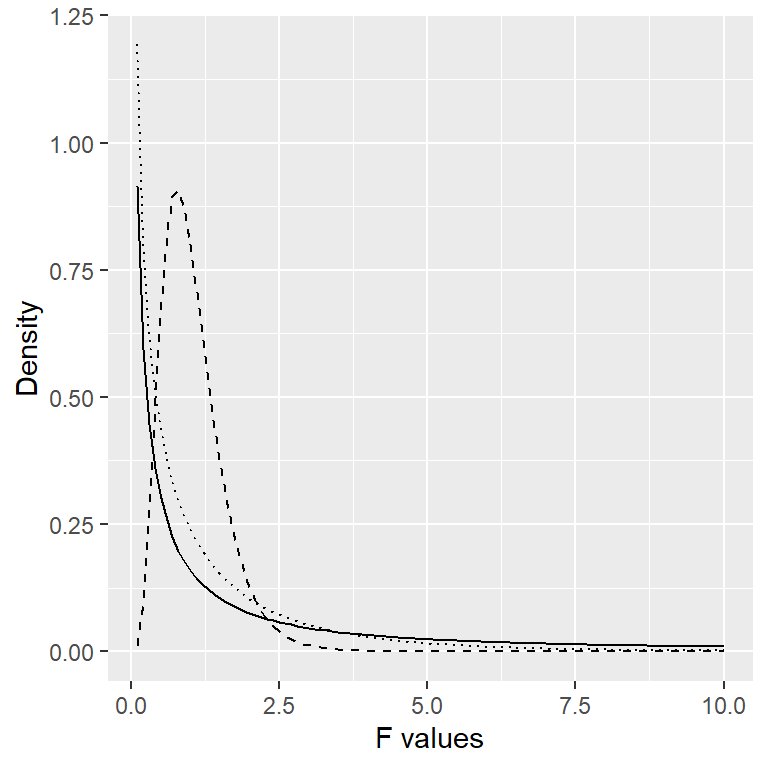
Distribuciones F bajo la hipótesis nula, para diferentes valores de los grados de libertad.

Figura 15.5: Distribuciones F bajo la hipótesis nula, para diferentes valores de los grados de libertad.

Para crear un modelo ANOVA, extendemos la idea de la codificación ficticia (dummy coding) que presentamos en el capítulo anterior. Recuerda que para la prueba t comparando dos medias, creamos una sola variable ficticia (dummy) que tomó el valor de 1 para una condición y cero para la otra. Aquí extendemos esa idea creando dos variables ficticias (dummy), una que codifica para la condición del Medicamento 1 y la otra que codifica para la condición del Medicamento 2. Justo como en la prueba t, tendremos una condición (en este caso, placebo) que no tiene una variable ficticia (dummy), y por lo tanto representa la línea base contra la cual las otras condiciones son comparadas; su media define la constante (origen) del modelo. Usando variables ficticias (dummy) para los medicamentos 1 y 2, podemos ajustar un modelo usando la misma aproximación que usamos en el capítulo anterior:

## 
## Call:
## lm(formula = sysBP ~ d1 + d2, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.084  -7.745  -0.098   7.687  23.431 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   141.60       1.66   85.50  < 2e-16 ***
## d1            -10.24       2.34   -4.37  2.9e-05 ***
## d2             -2.03       2.34   -0.87     0.39    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.9 on 105 degrees of freedom
## Multiple R-squared:  0.169,  Adjusted R-squared:  0.154 
## F-statistic: 10.7 on 2 and 105 DF,  p-value: 5.83e-05

La salida de este comando nos provee de dos cosas. Primero, nos muestra el resultado de una prueba t para cada una de las variables ficticias (dummy), que básicamente nos dice si cada una de las condiciones separadas difiere del placebo; parece que el Medicamento 1 lo hace, pero el Medicamento 2 no. Sin embargo, ten en cueta que si quisiéramos interpretar estas pruebas, necesitaríamos corregir los valores p para tomar en cuenta el hecho de que hemos realizado múltiples pruebas de hipótesis; veremos un ejemplo de cómo hacer esto en el siguiente capítulo.

Recuerda que la hipótesis que inicialmente queríamos probar era si había alguna diferencia entre cualquiera de las condiciones; llamamos a esto una prueba de hipótesis ómnibus, y es la prueba a la que se refiere el estadístico F. El estadístico F básicamente nos dice si nuestro modelo es mejor que un modelo simple que sólo incluye la constante. En este caso vemos que la prueba F es altamente significativa, consistente con nuestra impresión de que parece haber diferencias entre los grupos (que de hecho sabemos que sí las hay, porque nosotros creamos los datos).

15.7 Objetivos de aprendizaje

Después de leer este capítulo, deberías ser capaz de:

  • Describir el razonamiento detrás de la prueba de los signos.
  • Describir cómo se puede usar la prueba t para comparar una sola media contra un valor hipotetizado.
  • Comparar las medias de dos grupos independientes o relacionados usando una prueba t para dos muestras.
  • Describir cómo se puede usar el análisis de varianza para probar diferencias entre más de dos medias.

15.8 Apéndice

15.8.1 La prueba t de muestras relacionadas como un modelo lineal

También podemos definir la prueba t para muestras relacionadas en términos del modelo lineal general. Para hacer esto, incluimos todas las mediciones para cada participante como el conjunto de datos (dentro de un dataframe ordenado). Luego incluimos una variable en el modelo que codifique la identidad de cada persona (en este caso, la variable ID que contiene un ID para cada persona). Esto es conocido como un modelo mixto, porque incluye efectos de variables independientes así como efectos de individuos. El procedimiento para ajustar el modelo estándar lm() no puede hacer esto, pero podemos realizarlo usando la función lmer() del popular paquete lme4 en R, que se especializa en estimar modelos mixtos. La parte (1|ID) en la fórmula le dice a la función lmer() que estime una constante separada (que es a lo que se refiere el 1) para cada valor de la variable ID (i.e. para cada persona en el conjunto de datos), y luego que estime una pendiente común que relacione el momento en el tiempo con la presión sanguínea (BP, blood pressure).

# compute mixed model for paired test

lmrResult <- lmer(BPsys ~ timepoint + (1 | ID), 
                  data = NHANES_sample_tidy)
summary(lmrResult)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: BPsys ~ timepoint + (1 | ID)
##    Data: NHANES_sample_tidy
## 
## REML criterion at convergence: 2895
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.3843 -0.4808  0.0076  0.4221  2.1718 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  ID       (Intercept) 236.1    15.37   
##  Residual              13.9     3.73   
## Number of obs: 400, groups:  ID, 200
## 
## Fixed effects:
##                 Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)      121.370      1.118 210.361  108.55   <2e-16 ***
## timepointBPSys2   -1.020      0.373 199.000   -2.74   0.0068 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## tmpntBPSys2 -0.167

Puedes ver que esto nos muestra un valor p que es muy cercano al resultado de la prueba t para muestras relacionadas calculado usando la función t.test().