Capitulo 8 Remuestreo y Simulación

El uso de las simulaciones en computadora se ha convertido en un aspecto esencial de la estadística moderna. Por ejemplo, uno de los libros más importantes en informática práctica se llama “Recetas numéricas,” y recita lo siguiente:

“Si nos ofrecieran la opción entre tener el dominio de una estantería de cinco pies llena de libros de estadística y una mediana capacidad para realizar simulaciones estadísticas a lo Montecarlo, seguramente elegiríamos la segunda opción.”

En este capítulo hablaremos del concepto de una simulación Montecarlo y discutiremos cómo puede ser usada para realizar análisis estadísticos.

8.1 Simulación Montecarlo

El concepto de la simulación Montecarlo fue ideada por los matemáticos Stan Ulam y Nicholas Metropolis, quienes estuvieron trabajando para desarrollar un arma atómica para los Estados Unidos de América, como parte del Proyecto Manhattan. Necesitaban calcular el promedio de la distancia que recorrería un neutrón en una sustancia antes de que chocara con un núcleo atómico, pero no pudieron calcular esto usando matemáticas estándar. Ulam notó que estos cálculos podían ser simulados usando números aleatorios, justo como un juego de casino. En un juego de casino, como la ruleta, los números son generados de manera aleatoria; para estimar la probabilidad de un resultado específico, uno podría jugar el juego cientos de veces. El tío de Ulam había jugado en el casino Montecarlo en Mónaco, de ahí viene el nombre para esta nueva técnica.

Hay cuatro pasos a seguir para realizar una simulación Montecarlo:

1. Definir el dominio posible de los valores.
2. Generar números al azar dentro de ese dominio a partir de una distribución de probabilidad.
3. Realizar un cálculo usando números aleatorios .
4. Combinar los resultados a través de muchas repeticiones .

Como un ejemplo, digamos que quiero descubrir cuánto tiempo debo dejar para un test en clase. Pretenderemos por el momento que sabemos que la distribución del tiempo para completar el test es normal, con una media de 5 minutos y una desviación estándar de 1 minuto. Sabiendo esto, ¿qué tan extenso debe ser el periodo de tiempo para que esperemos que todos los estudiantes terminen el examen el 99% de las veces? Hay dos formas de resolver este problema. El primero es calculando la respuesta usando una teoría matemática conocida como estadística de valores extremos. No obstante, esto requiere matemáticas complejas. De forma alternativa, podríamos usar el método de Montecarlo. Para hacer esto, necesitamos generar muestras aleatorias obtenidas de una distribución normal.

8.2 Aleatoriedad en Estadística

El término “aleatorio” es usado coloquialmente para describir cosas que son bizarras o inesperadas, pero en estadística el término tiene un significado específico: Un proceso se considera aleatorio si es impredecible. Por ejemplo, si lanzo una moneda 10 veces, el valor del resultado de una vez que la lances no va a predecir el resultado de la segunda vez que la lances. Es importante destacar que el hecho de que algo es impredecible, no quiere decir que no es determinista. Por ejemplo, cuando lanzamos una moneda, el resultado de ésta está determinada por las leyes de la física; si supiéramos que todas las condiciones con suficiente detalle, podríamos predecir el resultado de cuando lancemos la moneda. De cualquier forma, son muchos factores los que se combinan para hacer el resultado del lanzamiento de la moneda impredecible en la práctica.

Lxs psicólogxs han demostrado que lxs humanxs tienen un sentido algo ineficiente para la aleatoriedad. En primera instancia, tendemos a ver patrones en donde no existen. De forma extrema, esto nos lleva al fenómeno de la pareidolia, en el cual las personas tienden a percibir objetos familiares en patrones aleatorios (como ver una nube con una rostro humano, o ver a la Vírgen María en un pedazo de pan tostado). En segunda instancia, lxs humanxs tienden a pensar en procesos aleatorios como una forma de auto-corrección, lo cual nos lleva a creer que vamos a ganar después de varias rondas de perder un juego de azar, un fenómeno llamado “la falacia del jugador.”

8.3 Generando números aleatorios

Hacer correr una simulación con el método de Montecarlo requiere que generemos números aleatorios. Para generar números genuinamente aleatorios (por ejemplo, números que son completamente impredecibles) es solamente posible a través de procesos físicos, como el decaimiento de átomos o el rodar unos dados, los cuales son difíciles de obtener o muy lentos como para que sean útiles en una simulación en computadora (aunque pueden obtenerse mediante NIST Randomness Beacon).

En general, en lugar de números verdaderamente aleatorios, podemos usar números pseudo-aleatorios, generados utilizando un algoritmo de computadora; estos números pueden aparentar ser aleatorios en el sentido de que son difíciles de predecir, pero las series de números eventualmente se repetirán en algún punto. Por ejemplo, el generador de números aleatorios utilizados en R se repetirán después de \(2^{19937} - 1\) números. Eso es mucho más que el número de segundos en la historia de universo, y generalmente pensamos que esto funciona para la mayoría de los propósitos en análisis estadísticos.

La mayoría de los softwares estadísticos incluyen funciones para generar números aleatorios para cada una de las grandes distribuciones de probabilidad, tal como la distribución uniforme (todos los valores entre 0 y 1 son igualmente probables), la distribución normal y la distribución binominal (por ejemplo, echar los dados o lanzar una moneda). La Figura 8.1 muestra ejemplos de números generados a partir de funciones de distribución uniformes y normales.

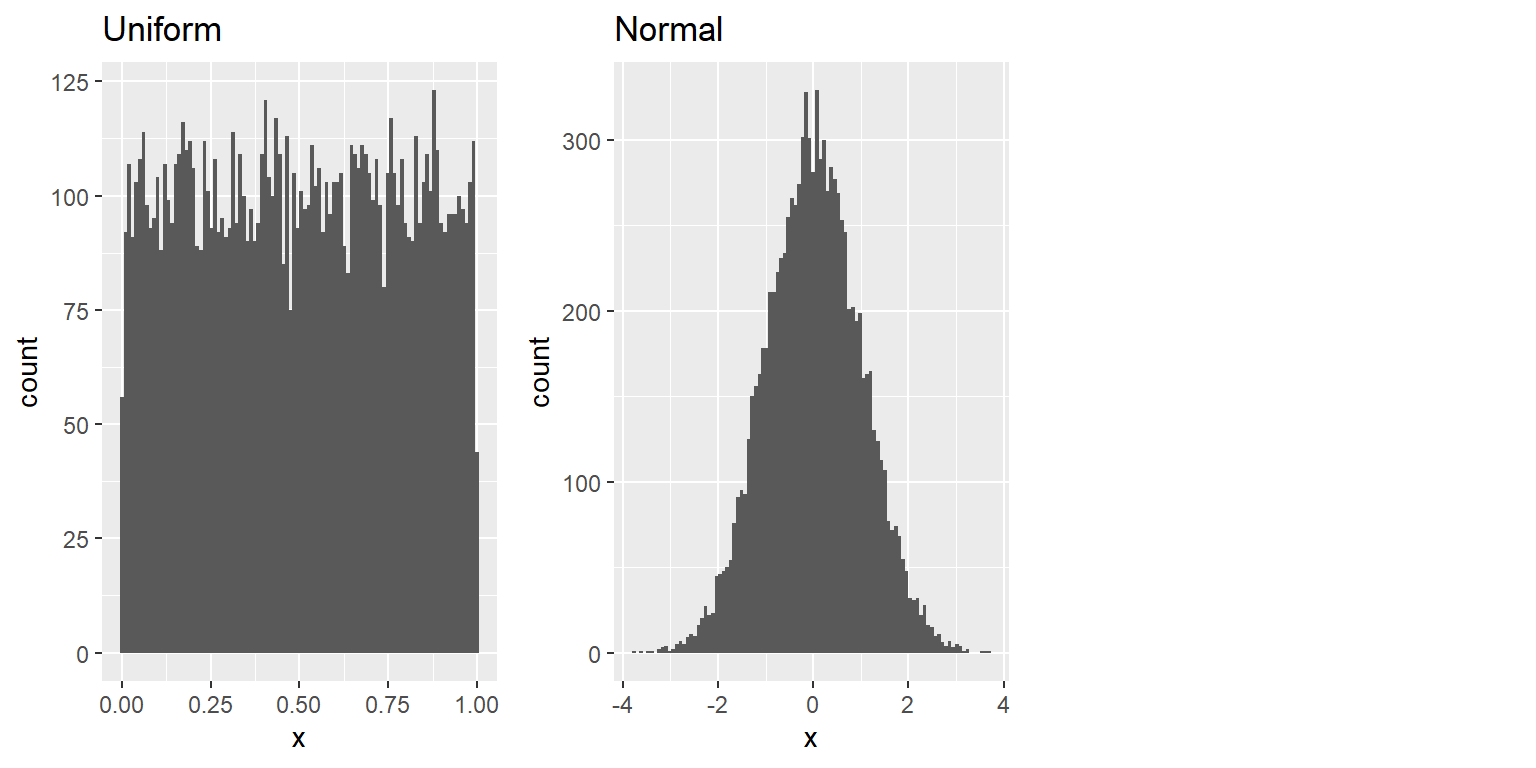
Figura 8.1: Ejemplos de números aleatorios generados a partir de una distribución uniforme (izquierda) y normal (derecha).

Unx puede también generar números aleatorios para cualquier distribución utilizando una función de cuantil para la distribución. Esto es lo inverso de la función de distribución cumulativa; en lugar de identificar las probabilidades cumulativas de un conjunto de valores, la función de cuantiles identifica los valores para un conjunto de probabilidades cumulativas. Usando la función de cuantiles, podemos generar números aleatorios de una distribución uniforme, y después mapearlos en la distribución de interés mediante su función de cuantil.

Por la forma en la que están creados, los generadores de números aleatorios en software estadísticos generan diferentes grupos de números aleatorios cada vez que los eches a correr. Sin embargo, también es posible que generen el mismo grupo de números aleatorios al configurar lo que se llama semilla aleatoria (o por su nombre en inglés random seed) en un valor específico. Haremos esto en muchos ejemplos en este libro, con el propósito de asegurarnos que los ejemplos sean reproducibles.

8.4 Utilizando una simulación con el Método de Montecarlo

Regresemos a nuestro ejemplo sobre los tiempos de finalización de un examen. Digamos que administro tres pruebas y grabo los tiempos en que cada alumno termina su examen, lo cual se vería como las distribuciones que se presentan en la Figura 8.2.

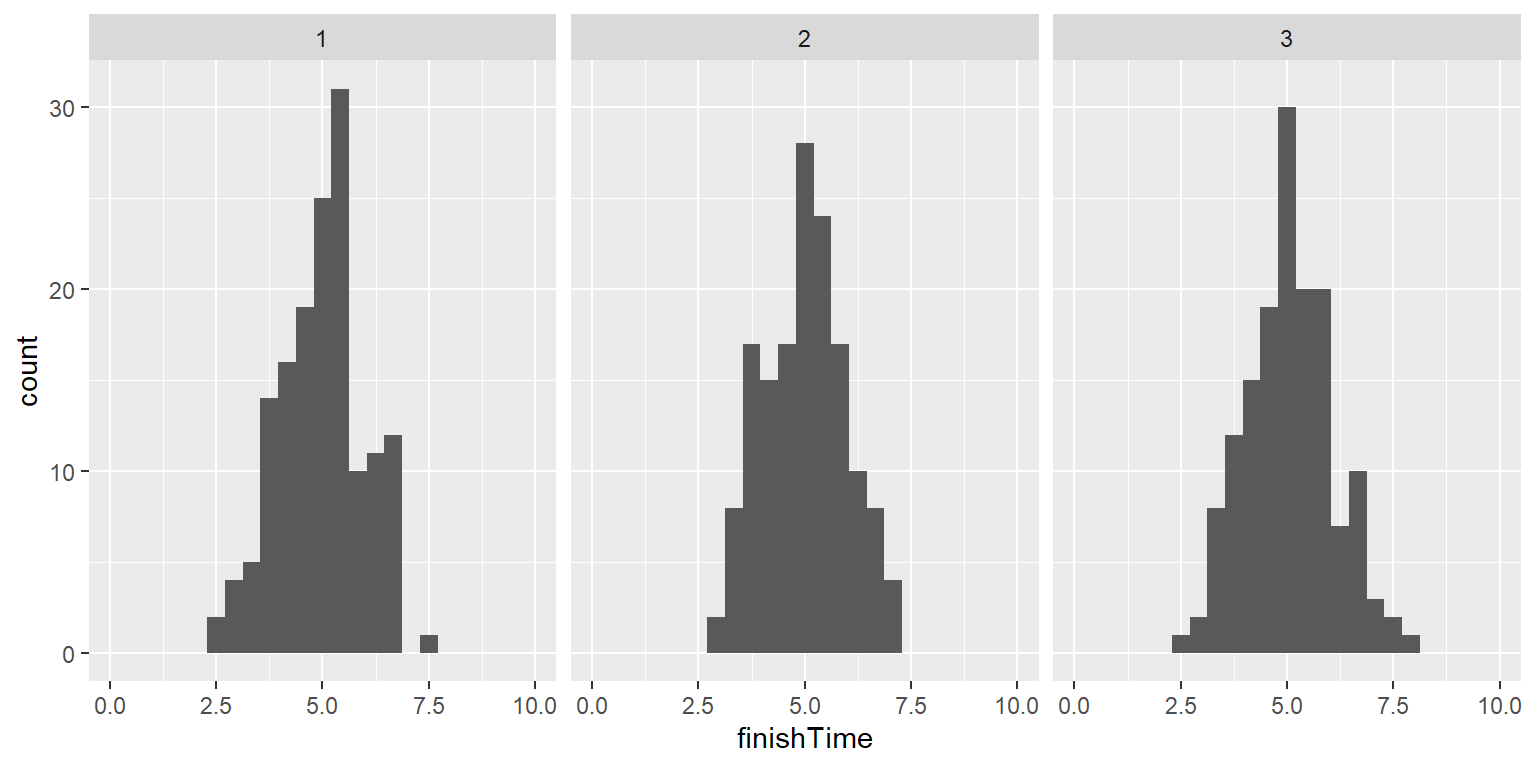
Figura 8.2: Distribuciones de simulaciones de tiempos de término del examen.

Lo que realmente queremos saber para contestar nuestra pregunta no es cómo se ve la distribución de los tiempos de finalización del examen, sino más bien cómo se ve la distribución del tiempo más largo de finalización de cada examen. Para hacer eso, podemos simular el tiempo de finalización para cada examen, asumiendo que los tiempos de finalización están distribuidos de forma normal, como hemos establecido arriba; para cada uno de estas simulaciones de examenes, después registramos el tiempo más largo de finalización. Repetimos esta simulación un gran número de veces (5000 debería ser suficiente) y luego registramos la distribución de los tiempos de finalización, lo cual se muestra en la Figura 8.3.

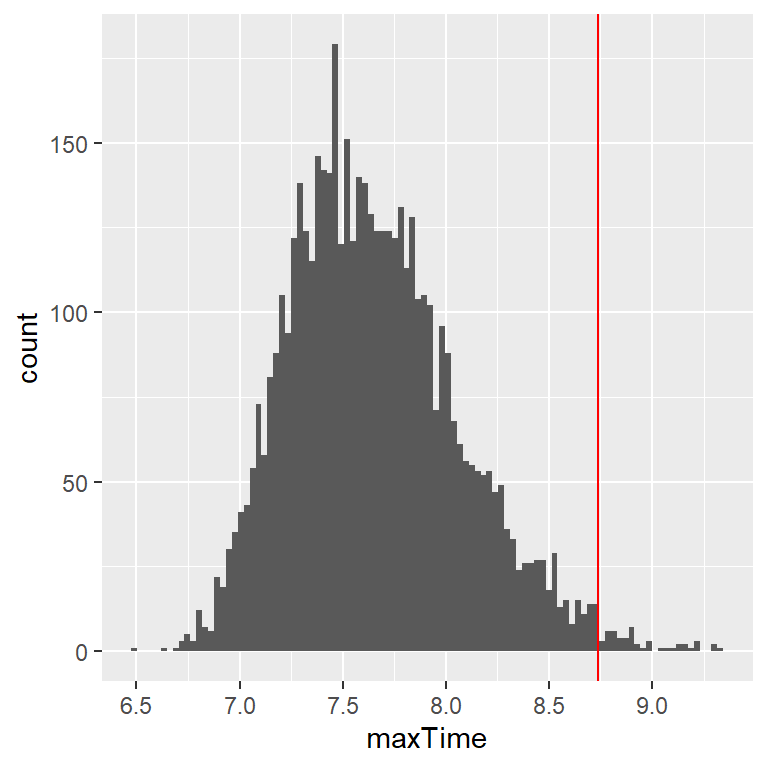
Figura 8.3: Distribución de tiempos máximos de finalización de examen a lo largo de diferentes simulaciones.

Esto muestra que el percentil número 99 de la distribución de la finalización del examen se encuentra en 8.74, lo cual significa que si diéramos esa cantidad de tiempo para el examen, entonces al menos el 99% de las veces todas las personas terminarían el examen a tiempo. Siempre es importante recordar que nuestras suposiciones importan– si están mal, entonces los resultados de la simulación serán inservibles. En este caso, asumimos que la distribución del tiempo de finalización estaba distribuido normalmente con una media y una desviación estándar en particular; si estas suposiciones son incorrectas (y casi ciertamente lo son, puesto que es raro que los tiempos de finalización tengan una distribución normal), entonces la respuesta real podría ser muy diferente.

8.5 Usando simulaciones para estadística: bootstrap

Hasta ahora hemos utilizado simulaciones para demostrar principios estadísticos, pero también podemos usar simulaciones para responder a preguntas estadísticas reales. En esta sección vamos a presentar un concepto conocido como el bootstrap (por su nombre en inglés, que no tiene traducción al español), este nos permite usar simulaciones para cuantificar la incertidumbre de estimaciones estadísticas. Más tarde en este curso, veremos otros ejemplos de cómo la simulación puede ser utilizada en muchas ocasiones para responder preguntas estadísticas, en especial, cuando los métodos de teoría estadística no están disponibles o sus suposiciones son muy difíciles de cumplir.

8.5.1 Calculando el bootstrap

En el capítulo anterior, utilizamos nuestro conocimiento del muestreo de la distribución de la media para calcular el error estándar de la media. Pero ¿qué pasa si no podemos asumir que las estimaciones están distribuidas de forma normal, o si no sabemos su distribución? La idea del bootstrap es usar los mismos datos para estimar la respuesta. El nombre viene de la idea de levantarse a unx mismx por las agujetas de sus propias botas, expresando la idea de que no necesitamos herramientas externas para utilizar como palanca, así que tenemos que asirnos de los mismos datos. El método boostrap fue acuñado por Bradley Efron en el Departamento de Estadística de Stanford, quien es uno de los estadísticos más influyentes del mundo.

La idea detrás del bootstrap es que repetidamente tomamos muestras del conjunto de datos real; lo que es más importante, muestreamos con reemplazo, de modo que el mismo punto de datos a menudo terminará representado varias veces en una de las muestras. Después calculamos nuestro estadístico de interés en cada una de las muestras del bootstrap, y utilizamos la distribución de esos estimados como nuestra distribución muestral. En cierto sentido, tratamos a nuestra muestra como si fuera la población completa, y luego muestreamos repetidamente con reemplazo para generar nuestras muestras para el análisis. Esto se basa en la suposición de que nuestra muestra particular es una representación precisa de la población, lo cual es razonablemente probable para muestras grandes, pero puede quebrantarse cuando las muestras son pequeñas.

Comencemos utilizando el bootstrap para estimar la distribución muestral de la media de alturas de personas adultas en la base de datos NHANES, para que podamos comparar el resultado del error estándar de la media (SEM, standard error of the mean), que mencionamos hace unos momentos.

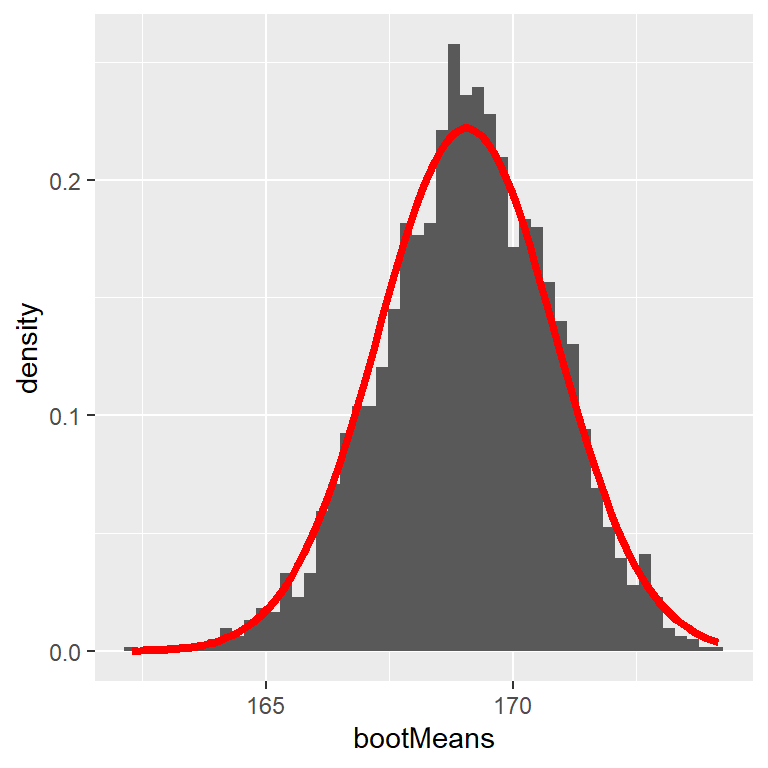
Figura 8.4: Un ejemplo de cálculo de boostrap del error estándar de la media (SEM) de altura de personas adultas en la base de datos NHANES. El histograma muestra la distribución de las medias a lo largo de las diferentes muestras bootstrap, mientras que la línea roja muestra la distribución normal basada en la media y desviación estándar de la muestra.

La Figura 8.4 muestra que la distribución de la media a través de las muestras del bootstrap es muy cercana al estimado teórico basado en la suposición de normalidad. Usualmente no usaríamos el bootstrap para calcular intervalos de confianza de la media (puesto que generalmente podemos asumir que la distribución normal es apropiada para la distribución muestral de la media, siempre y cuando nuestra muestra sea lo suficientemente grande), pero este ejemplo muestra cómo este método nos brinda aproximadamente el mismo resultado que el método estándar basado en la distribución normal. El bootstrap sería más comúnmente usado para generar errores estándar para estimaciones de otros estadísticos donde sabemos o sospechamos que la distribución normal no es apropiada. Además, en un capítulo posterior revisarás cómo podemos usar también muestras de bootstrap para generar estimaciones de incertidumbre del estadístico de nuestra muestra.

8.6 Objetivos de aprendizaje

Después de haber leído este capítulo, deberías ser capaz de:

• Describir el concepto del método de Montecarlo.
• Describir el significado de la aleatoriedad en estadística.
• Describir cómo son generados los números pseudo-aleatorios.
• Describir el concepto de bootstrap.

8.7 Lecturas sugeridas

• Computer Age Statistical Inference: Algorithms, Evidence and Data Science, por Bradley Efron y Trevor Hastie.